Magnetic field reconstruction at test mass using the multi-stage bias correction model
-
摘要:
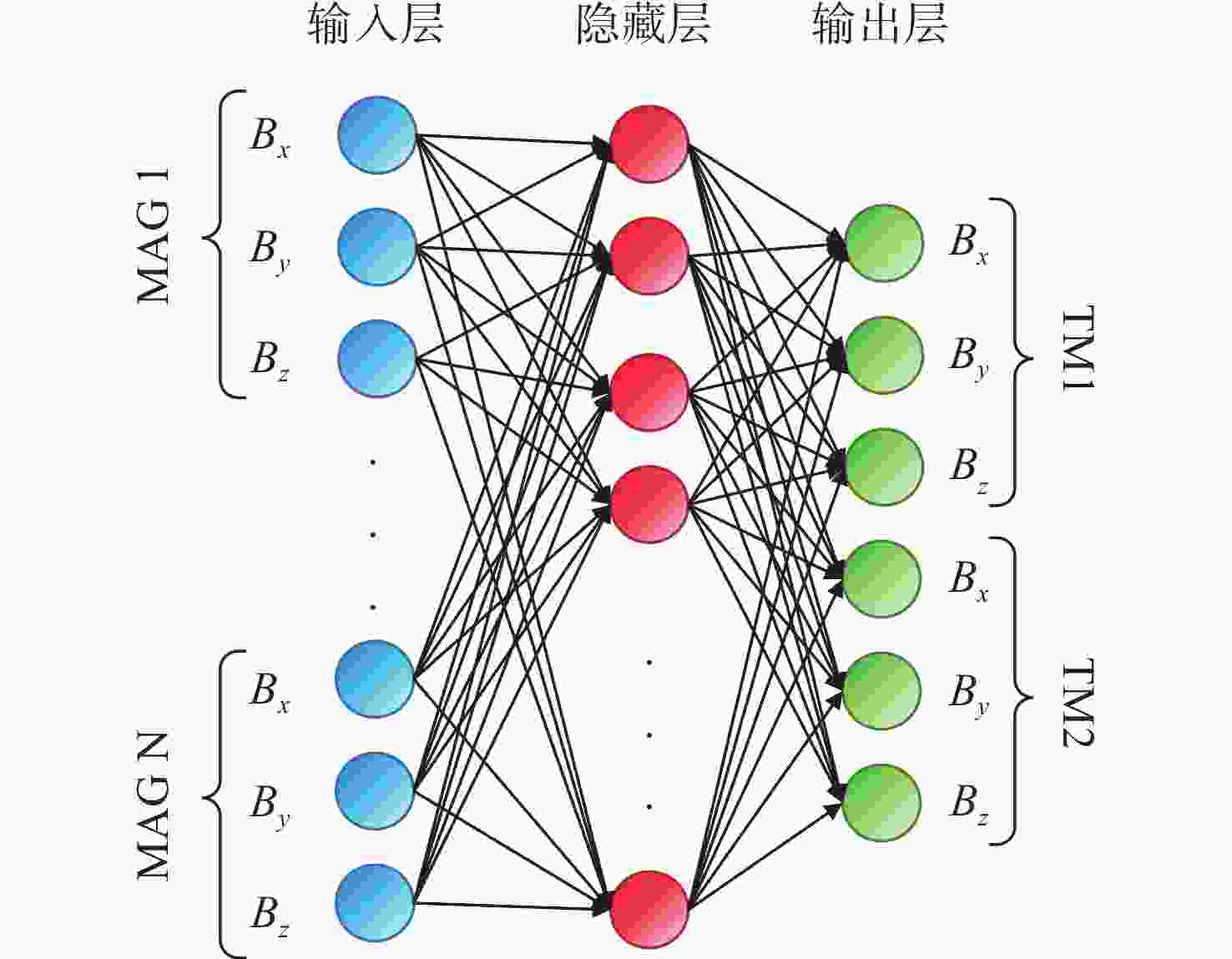
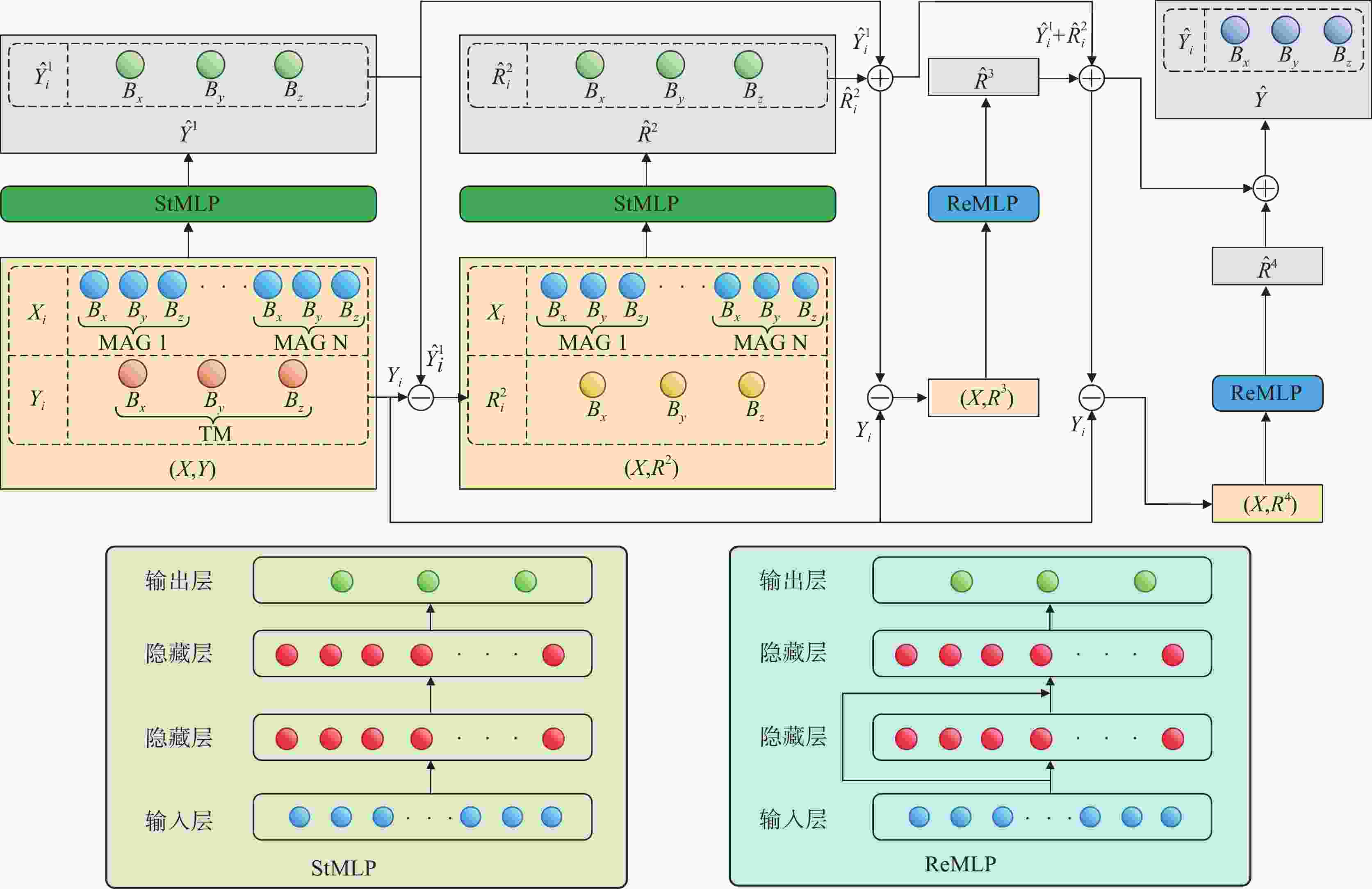
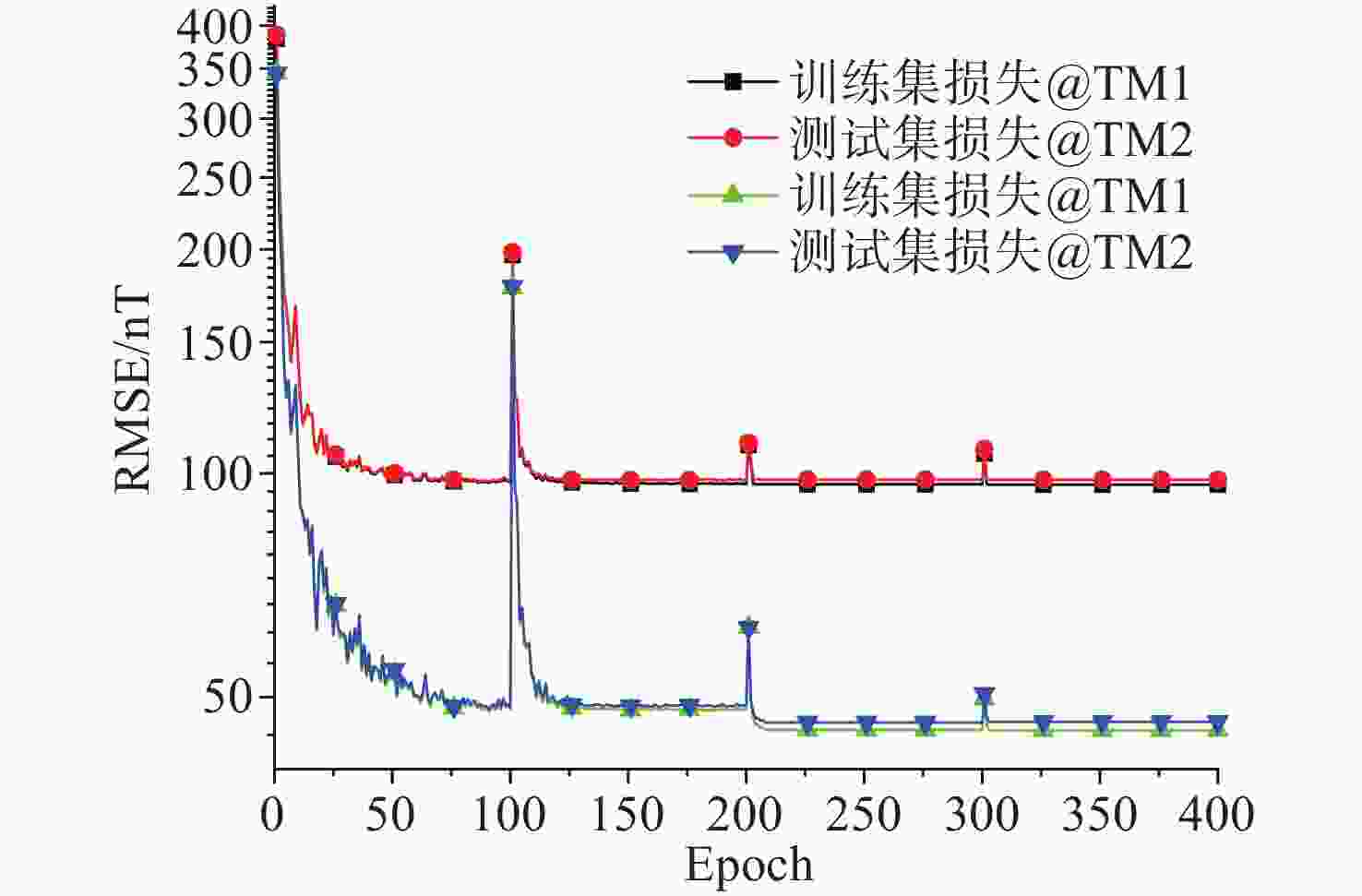
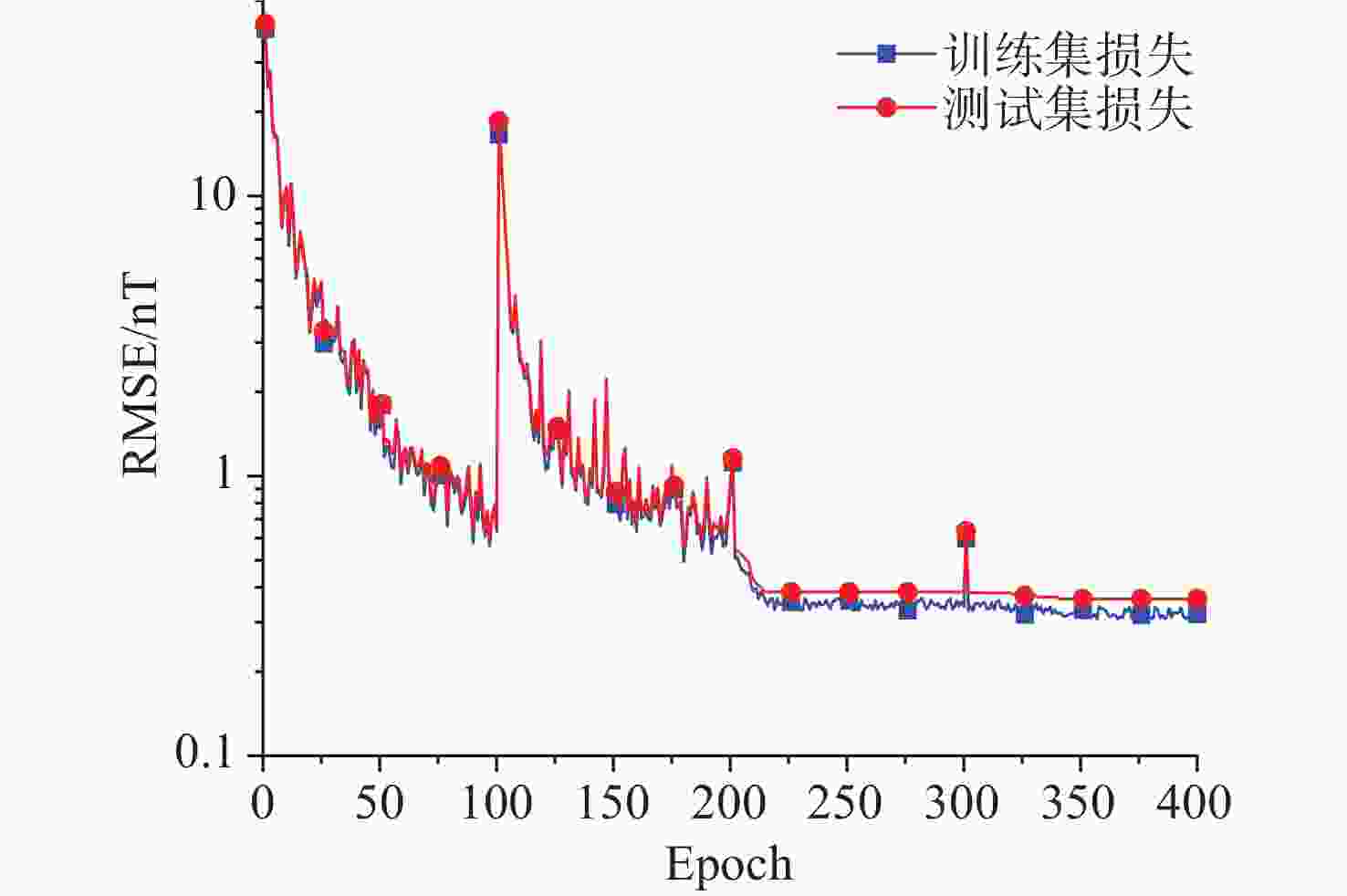
为了精确评估空间引力波探测任务中检验质量所受到的磁场波动、磁场梯度波动噪声,本文提出了多阶段偏差修正模型MSBCM对检验质量处磁场进行精确重建。在集成学习方法的基础上,本文构建了标准全连接神经网络模块和残差全连接神经网络模块作为多阶段偏差修正模型的弱预测模型。每个弱预测模型都将对前序模型的预测偏差进行修正,最终构成强预测模型,实现对检验质量处磁场的精确重建。在对LISA Pathfinder、eLISA和太极二号空间引力波探测航天器的检验质量处的磁场重建实验中,与其他方法相比MSBCM方法在敏感轴方向的平均相对误差最小。模拟在轨实验中,MSBCM方法重建检验质量1敏感轴方向的磁场波动和磁场梯度波动加速度噪声的均方根误差分别为1.68×10−17 (m/s2/Hz1/2)和4.00×10−17 (m/s2/Hz1/2)。此外,MSBCM在重建检验质量2敏感轴方向的磁场波动和磁场梯度加速度噪声的均方根误差仅次于距离加权法,分别为1.72×10−16 (m/s2/Hz1/2) 和2.93×10−16 (m/s2/Hz1/2),充分验证了本文提出方法在评估在轨空间引力波探测检验质量处磁场的优势。
Abstract:To precisely evaluate the noise induced by magnetic field and magnetic field gradient fluctuations acting on the test masses in space gravitational wave detection missions, a Multi-stage Bias Correction Model (MSBCM) is proposed for the accurate reconstruction of the magnetic fields at the test mass. Based on the ensemble learning method, the standard fully connected neural network modules and residual fully connected neural network modules are constructed as weak predictors for the MSBCM. Each weak predictor sequentially corrects the prediction biases from the preceding model, cumulatively forming a robust predictive model to realize precise magnetic field reconstruction at test mass locations. Magnetic field reconstruction experiments conducts on the LISA Pathfinder, eLISA, and Taiji-2 space gravitational wave detection spacecraft, and the proposed MSBCM method demonstrates the lowest mean relative errors along sensitive axes in comparison with other interpolation or estimation methods. In simulating on-orbit experiments, the MSBCM method achieves the root mean square error of magnetic field fluctuations and gradient fluctuations in acceleration noise on the sensitive axis of test mass 1 of 1.68×10−17 (m/s2/Hz1/2) and 4.00×10−17 (m/s2/Hz1/2), respectively. Additionally, MSBCM closely only to the distance weighted method in minimizing the root mean square error for magnetic field fluctuations and gradient acceleration noise on the sensitive axis of test mass 2, records at 1.72×10−16 (m/s2/Hz1/2) and 2.93×10−16 (m/s2/Hz1/2), further validating the advantages of the proposed method in assessing magnetic fields around test masses in space-based gravitational wave detection missions.
-
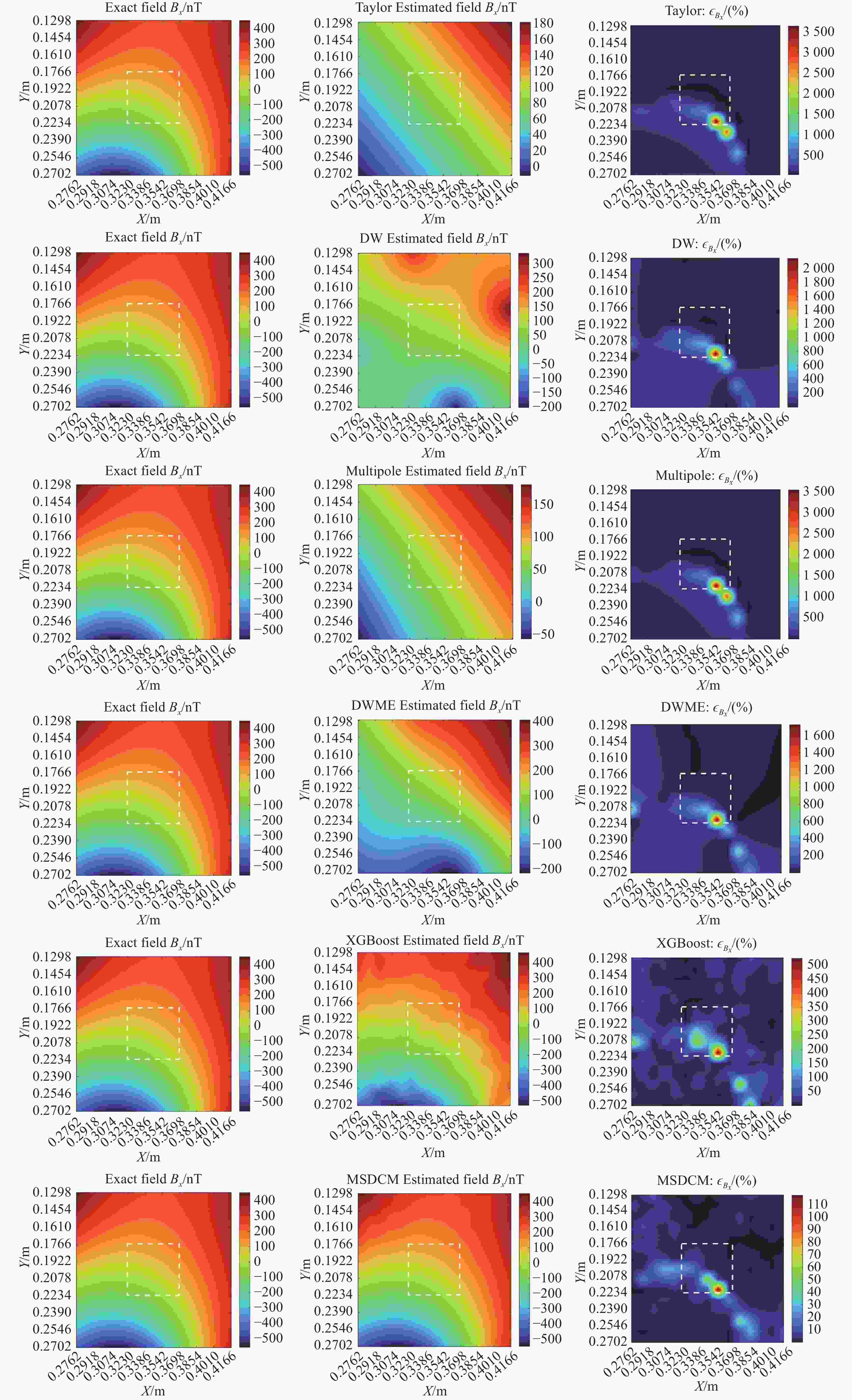
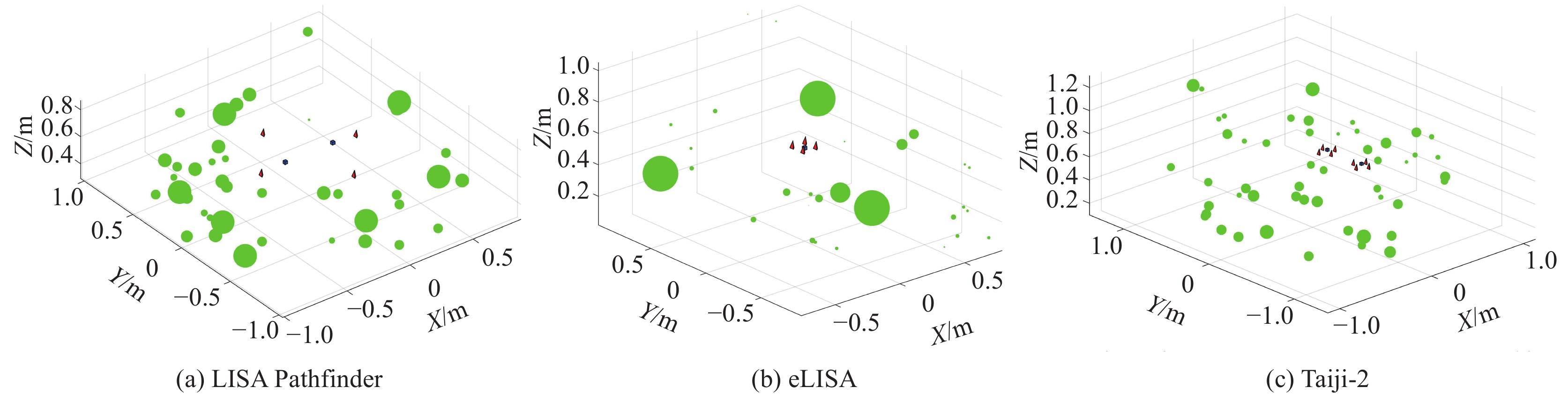
表 1 LISA Pathfinder磁场重建结果
Table 1. Magnetic field reconstruction results for LISA Pathfinder
方法 ${\bar \varepsilon _{\boldsymbol{B}}}$/% ${\varepsilon _{{\boldsymbol{B}},{\mathrm{max}}}}$/% |B| Bx By Bz |B| Bx By Bz TM1 Taylor 89.25 518.92 564.37 694.50 2745.34 573610.11 604412.84 2461076.40 WD 126.26 646.60 637.91 798.67 3767.01 477011.43 739996.09 2450750.40 Multipole 85.51 523.51 524.85 647.88 3452.78 467206.45 759302.88 1998534.80 DWME 113.38 616.28 663.83 723.73 3645.20 451613.53 1097369.80 1873063.70 XGBoost 86.30 755.93 884.03 1378.01 5161.49 440535.35 617789.70 3250015.40 MSBCM 26.57 201.07 231.66 212.58 1055.81 131405.62 325384.40 327050.17 TM2 Taylor 206.23 1477.86 1385.79 2117.36 6337.63 2501042.40 1602870.80 6981814.10 WD 270.93 1749.38 1998.34 1929.93 5561.22 2664887.90 3045968.80 3634591.40 Multipole 203.87 1434.70 1624.28 1774.25 5552.77 1994890.20 2521400.00 4399474.20 DWME 249.19 1627.78 1920.93 1561.21 5248.44 2215714.60 2922788.10 1403577.60 XGBoost 19.29 210.34 255.02 203.20 1305.22 438854.54 217929.15 279339.43 MSBCM 18.32 220.39 215.91 200.62 1418.04 612493.07 140519.40 412914.94 表 2 eLISA磁场重建结果
Table 2. Magnetic field reconstruction results for eLISA
方法 ${\bar \varepsilon _{\boldsymbol{B}}}$/% ${\varepsilon _{{\boldsymbol{B}},{\mathrm{max}}}}$/% |B| Bx By Bz |B| Bx By Bz Taylor 0.84 2.50 3.18 3.54 6.85 1590.39 13222.55 5296.21 WD 0.84 2.50 3.18 3.54 6.85 1590.39 13222.55 5296.21 Multipole 1.01 2.98 3.13 3.64 6.75 1766.27 8960.39 5552.00 DWME 1.01 2.98 3.13 3.64 6.75 1766.27 8960.39 5552.00 XGBoost 1.21 8.68 10.65 8.65 25.00 10906.87 22410.27 4816.18 MSBCM 0.18 1.53 1.30 2.42 3.49 1177.87 2822.87 2453.91 表 3 太极二号磁场重建结果
Table 3. Magnetic field reconstruction results for Taiji-2
方法 ${\bar \varepsilon _{\boldsymbol{B}}}$/% ${\varepsilon _{{\boldsymbol{B}},{\mathrm{max}}}}$/% |B| Bx By Bz |B| Bx By Bz TM1 Taylor 15.11 84.79 123.55 207.12 887.44 33066.14 48781.65 425602.34 WD 8.83 48.06 99.05 158.43 743.90 29353.64 45913.87 282891.87 Multipole 11.74 55.34 111.75 185.63 706.02 15681.89 52423.43 362661.43 DWME 15.61 79.26 123.28 201.89 1025.87 33688.57 62955.00 374511.89 XGBoost 3.42 29.92 24.38 37.60 181.28 19632.57 22803.73 104671.03 MSBCM 1.35 12.87 10.82 14.38 145.24 7294.00 6317.08 30633.32 TM2 Taylor 15.33 115.74 142.19 153.31 442.41 108830.68 185920.57 155773.28 WD 8.71 73.17 104.46 115.51 216.97 104259.11 107441.89 92245.70 Multipole 11.82 74.48 123.59 134.94 341.09 44944.78 118690.82 131479.33 DWME 15.69 113.35 133.23 147.43 371.93 88090.07 153712.76 144410.41 XGBoost 2.94 22.81 23.38 23.01 55.46 8802.75 16855.77 37746.41 MSBCM 1.10 13.85 11.77 12.48 23.77 19169.06 29637.80 13418.15 表 4 不同方法重建磁场波动、梯度波动噪声的RMSE
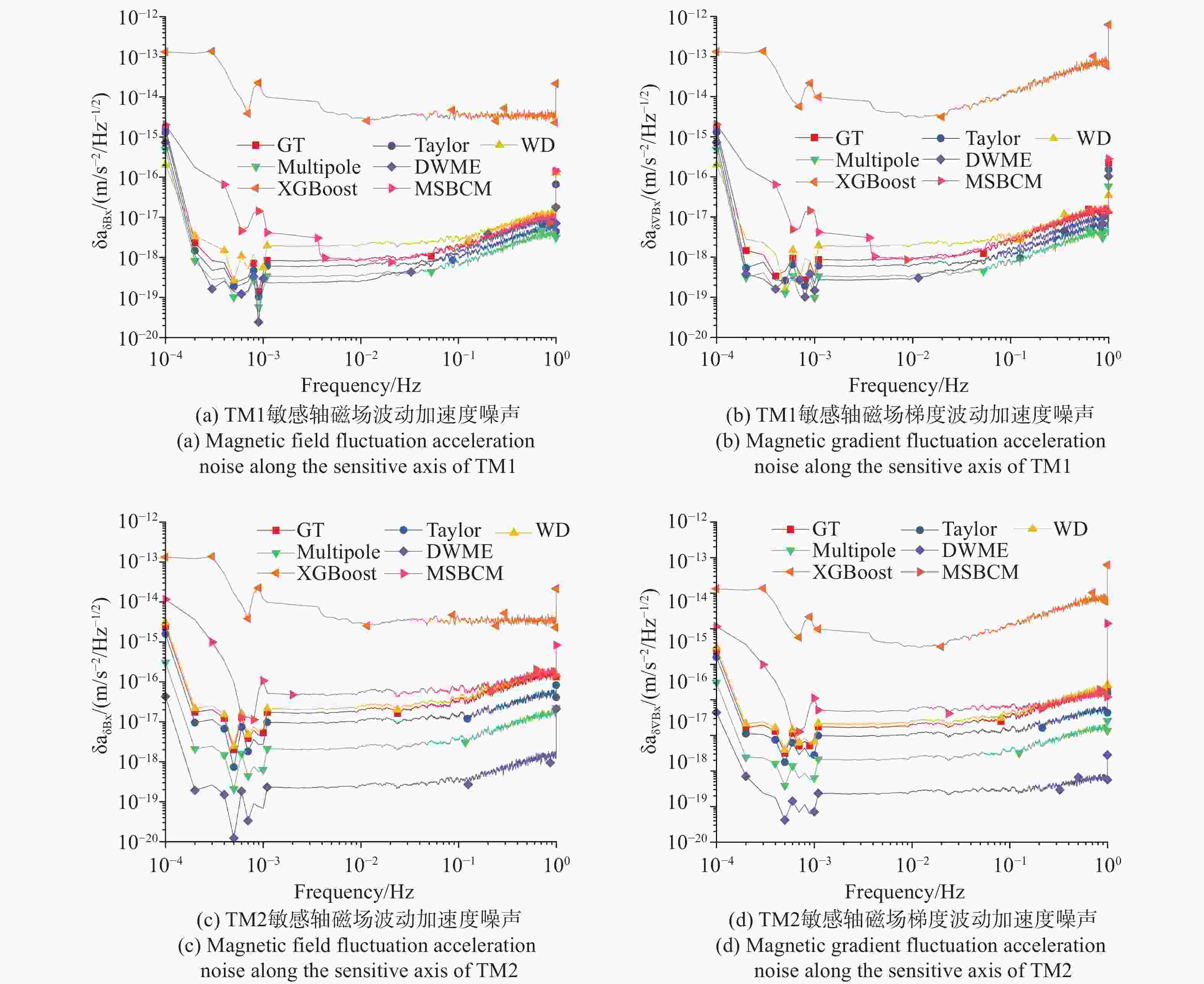
Table 4. RMSE of magnetic field fluctuations and magnetic gradient fluctuations using different methods
方法 RMSE (${\mathrm{m}}\cdot {\mathrm{s}}^{-2}{\mathrm{Hz}}^{-\tfrac{1}{2}} $) $\delta {a_{\delta {B_x}}}$ $\delta {a_{\delta \nabla {B_x}}}$ TM1 Taylor 3.47×10−17 6.42×10−17 WD 2.74×10−17 1.28×10−16 Multipole 9.17×10−17 1.10×10−16 DWME 5.98×10−17 5.83×10−17 XGBoost 4.63×10−15 7.48×10−14 MSBCM 1.68×10-17 4.00×10-17 TM2 Taylor 3.02×10−16 3.47×10−16 WD 9.39×10-17 2.42×10-16 Multipole 4.06×10−16 8.97×10−16 DWME 4.47×10−16 1.02×10−15 XGBoost 4.49×10−15 7.41×10−14 MSBCM 1.72×10−16 2.93×10−16 表 5 消融实验
Table 5. Ablation study
方法 弱预测模型 ${\bar \varepsilon _{\boldsymbol{B}}}$/% Bx (TM1) Bx (TM2) MSBCM StMLP 20.76 24.01 StMLP 19.68 22.41 ReMLP 16.01 14.58 ReMLP 13.85 12.87 模型一 StMLP 20.76 24.01 StMLP 19.68 22.41 StMLP-LM 15.24 14.92 StMLP-LM 13.49 14.44 模型二 StMLP 20.76 24.01 StMLP 19.68 22.41 StMLP 17.21 17.48 StMLP 15.55 14.35 -
[1] ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102 [2] WANNER G. Space-based gravitational wave detection and how LISA Pathfinder successfully paved the way[J]. Nature Physics, 2019, 15(3): 200-202. doi: 10.1038/s41567-019-0462-3 [3] SALA L. Residual test mass acceleration in LISA Pathfinder: in-depth statistical analysis and physical sources[D]. Trento: University of Trento, 2023. [4] ZHANG H Y, XU P, YE Z Q, et al. A systematic approach for inertial sensor calibration of gravity recovery satellites and its application to Taiji-1 mission[J]. Remote Sensing, 2023, 15(15): 3817. doi: 10.3390/rs15153817 [5] 宋长孝, 于信, 白素平, 等. 光轴稳定探测系统无热化光机结构设计[J]. 中国光学(中英文),2024,17(4):909-920. doi: 10.37188/CO.2023-0226SONG CH X, YU X, BAI S P, et al. Design of athermalization optical machine structure for optical axis stability detection system[J]. Chinese Optics, 2024, 17(4): 909-920. (in Chinese). doi: 10.37188/CO.2023-0226 [6] 郭蕊香, 贾晓军, 谢常德, 等. 实用化多功能光压缩器[J]. 物理学报,2002,51(6):1262-1267. doi: 10.3321/j.issn:1000-3290.2002.06.022GUO R X, JIA X J, XIE CH D, et al. Compact nonclassical light source——“Squeezer”[J]. Acta Physica Sinica, 2002, 51(6): 1262-1267. (in Chinese). doi: 10.3321/j.issn:1000-3290.2002.06.022 [7] CAÑIZARES P, CONCHILLO A, GARCÍA-BERRO E, et al. The diagnostics subsystem on board LISA pathfinder and LISA[J]. Classical and Quantum Gravity, 2009, 26(9): 094005. doi: 10.1088/0264-9381/26/9/094005 [8] MATEOS I, DIAZ-AGUILÓ M, GESA L, et al. Magnetic field measurement using chip-scale magnetometers in eLISA[C]. Journal of Physics: Conference Series, IOP Publishing, 2015: 012028. [9] MATEOS I, RAMOS-CASTRO J, LOBO A. Low-frequency noise characterization of a magnetic field monitoring system using an anisotropic magnetoresistance[J]. Sensors and Actuators A: Physical, 2015, 235: 57-63. doi: 10.1016/j.sna.2015.09.021 [10] DIAZ-AGUILÓ M, GARCÍA-BERRO E, LOBO A. Theory and modelling of the magnetic field measurement in LISA PathFinder[J]. Classical and Quantum Gravity, 2010, 27(3): 035005. doi: 10.1088/0264-9381/27/3/035005 [11] MATEOS I, DÍAZ-AGUILÓ M, RAMOS-CASTRO J, et al. Interpolation of the magnetic field at the test masses in eLISA[J]. Classical and Quantum Gravity, 2015, 32(16): 165003. doi: 10.1088/0264-9381/32/16/165003 [12] LIU B B, YANG ZH, QIANG L E, et al. Magnetic field recovery technique based on distance weighting multipole expansion method[J]. Europhysics Letters, 2023, 143(5): 59003. doi: 10.1209/0295-5075/acf51f [13] SPANTIDEAS S T, CAPSALIS C N. Validation of a source identification method for prediction of low-frequency magnetic fields in space missions[J]. IEEE Magnetics Letters, 2018, 9: 1-5. [14] TROUGNOU L. Ecss space systems electromagnetic compatibility handbook[C]. 2012 ESA Workshop on Aerospace EMC, IEEE, 2012: 1-6. [15] TSATALAS S, VERGOS D, SPANTIDEAS S T, et al. A novel multi-magnetometer facility for on-ground characterization of spacecraft equipment[J]. Measurement, 2019, 146: 948-960. doi: 10.1016/j.measurement.2019.07.016 [16] JACKSON J D. Classical Electrodynamics[M]. New York: Wiley, 1999. [17] 柴国志, 黄亮, 乔亮, 等. 星上剩磁对惯性传感器的影响[J]. 中国光学,2019,12(3):515-525. doi: 10.3788/co.20191203.0515CHAI G ZH, HUANG L, QIAO L, et al. Effect of the on-board residual magnetism on inertial sensors[J]. Chinese Optics, 2019, 12(3): 515-525. (in Chinese). doi: 10.3788/co.20191203.0515 [18] VITALE S. Effect of eddy currents on down-conversion of magnetic noise[J]. Memo LISA Technology Package, 2007. [19] TROUGNOU L. Ac magnetic susceptibility of LisaPF test masses[R]. ESTEC, 2007. [20] FERTIN D, TROUGNOU L. LisaPF test masses acceleration noise due to eddy currents[R]. ESTEC, 2007. [21] YANG F C, BAI Y ZH, HONG W, et al. A charge control method for space-mission inertial sensor using differential UV LED emission[J]. Review of Scientific Instruments, 2020, 91(12): 124502. doi: 10.1063/5.0013232 [22] SUMNER T J, MUELLER G, CONKLIN J W, et al. Charge induced acceleration noise in the LISA gravitational reference sensor[J]. Classical and Quantum Gravity, 2020, 37(4): 045010. doi: 10.1088/1361-6382/ab5f6e [23] TASKINEN J, YLIRUUSI J. Prediction of physicochemical properties based on neural network modelling[J]. Advanced Drug Delivery Reviews, 2003, 55(9): 1163-1183. doi: 10.1016/S0169-409X(03)00117-0 [24] DIAZ-AGUILO M, LOBO A, GARCÍA–BERRO E. Neural network interpolation of the magnetic field for the LISA Pathfinder Diagnostics Subsystem[J]. Experimental Astronomy, 2011, 30(1): 1-21. doi: 10.1007/s10686-011-9215-8 [25] XU L. A proportional differential control method for a time-delay system using the Taylor expansion approximation[J]. Applied Mathematics and Computation, 2014, 236: 391-399. doi: 10.1016/j.amc.2014.02.087 [26] SHEVTSOVA I. On the accuracy of the approximation of the complex exponent by the first terms of its Taylor expansion with applications[J]. Journal of Mathematical Analysis and Applications, 2014, 418(1): 185-210. doi: 10.1016/j.jmaa.2014.03.075 [27] LU G Y, WONG D W. An adaptive inverse-distance weighting spatial interpolation technique[J]. Computers & Geosciences, 2008, 34(9): 1044-1055. [28] ALAEE R, ROCKSTUHL C, FERNANDEZ-CORBATON I. An electromagnetic multipole expansion beyond the long-wavelength approximation[J]. Optics Communications, 2018, 407: 17-21. doi: 10.1016/j.optcom.2017.08.064 [29] HE K M, ZHANG X Y, REN SH Q, et al. Deep residual learning for image recognition[C]. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2016: 770-778. [30] RANGANATHAN A. The levenberg-marquardt algorithm[J]. Tutoral on LM algorithm, 2004, 11(1): 101-110. [31] CHEN T Q, GUESTRIN C. XGBoost: a scalable tree boosting system[C]. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, 2016: 785-794. [32] MATEOS I, DIAZ-AGUILÓ M, GIBERT F, et al. Magnetic back action effect of magnetic sensors for eLISA/NGO[C]. 9th International LISA Symposium, ASP, 2013: 341-345. [33] STONE E C, FRANDSEN A M, MEWALDT R A, et al. The advanced composition explorer[J]. Space Science Reviews, 1998, 86(1-4): 1-22. [34] KESKAR N S, SOCHER R. Improving generalization performance by switching from Adam to SGD[J]. arXiv: 1712.07628, 2017. -





 下载:
下载: