-
摘要:
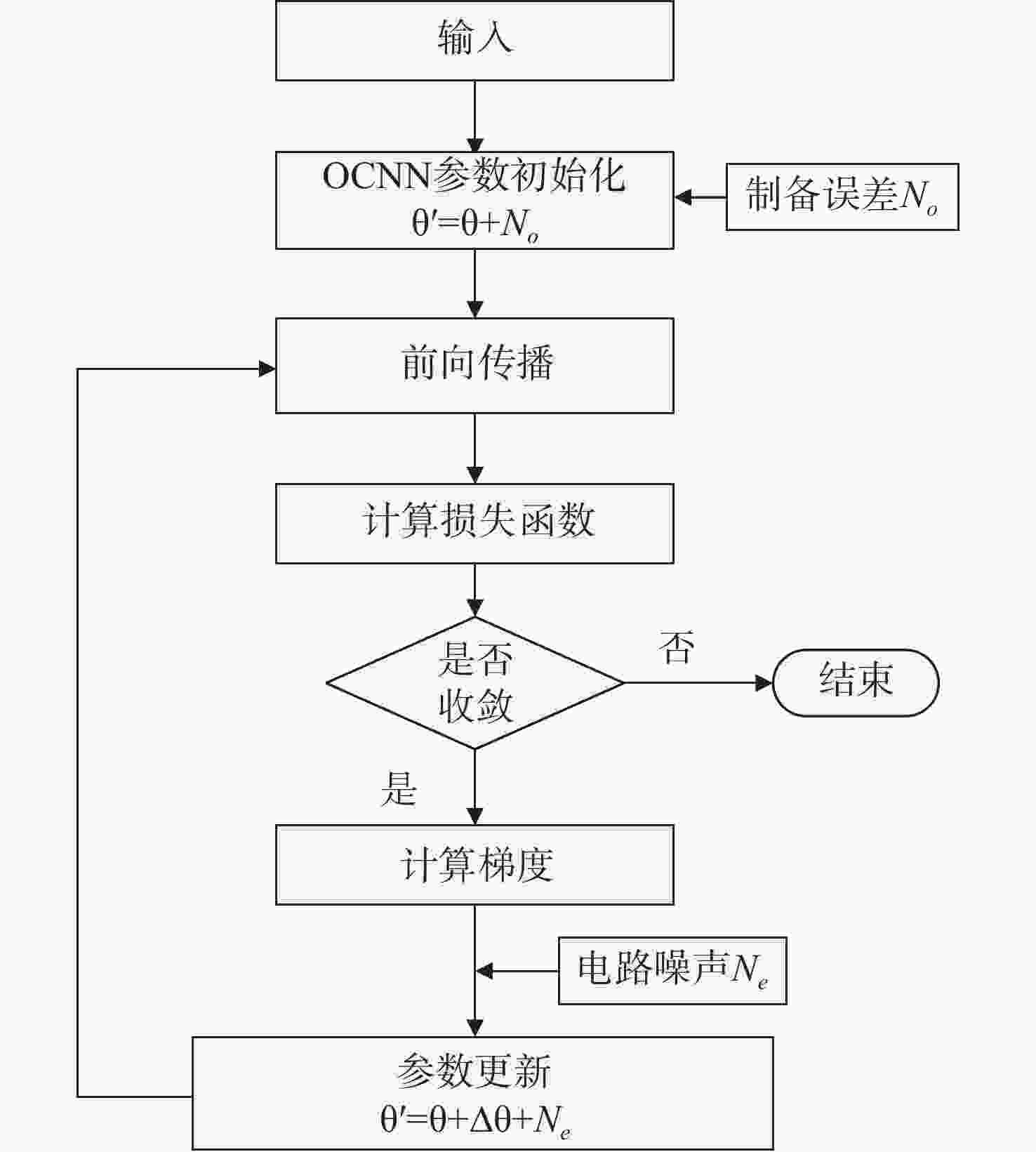
光电混合的光学卷积神经网络（OCNN）通过结合光子元件的并行线性计算能力和电子元件的非线性处理优势，在分类任务中展现了巨大的潜力。然而，光子元件的制备误差即不精确性和执行后向传播的FPGA中电路噪声显著影响了网络性能。本文搭建了光电混合的OCNN，其中的线性计算由基于马赫-曾德尔干涉仪的光学计算层完成，而池化计算及训练过程在FPGA中完成。本文着重研究了在FPGA上的片上训练方案，分析了噪声对片上训练效果的影响，并提出了增强OCNN抗噪能力的网络优化策略。具体地，通过调整池化方式和尺寸以增强OCNN的抗噪性能，并在池化层后引入Dropout正则化以进一步提升模型的识别准确率。实验结果表明，本文采用的片上训练方案能够有效修正光子元件的不精确性带来的误差，但电路噪声是限制OCNN性能的主要因素。此外，当电路噪声较大时，例如当电路噪声造成的MZI相位误差标准差为0.003，最大池化方式与Dropout正则化的结合可以显著提升OCNN的测试准确率（最高达78%）。本研究为实现OCNN的片上训练提供了重要的参考依据，同时为光电混合架构在高噪声环境下的实际应用探索提供了新的思路。
Abstract:The hybrid optical-electronic optical convolutional neural network (OCNN) combines the parallel linear computation capabilities of photonic devices with the nonlinear processing advantages of electronic components, demonstrating significant potential in classification tasks. However, the fabrication inaccuracies of photonic devices and the circuit noise in FPGA-based backpropagation notably degrade the network performance. In this work, the hybrid OCNN is constructed, where the linear computations are performed by optical computing layers based on Mach-Zehnder interferometers (MZIs), while the pooling operations and the training process are implemented on the FPGA. This study focuses on the feasibility of on-chip training on FPGA, analyzing the impact of noise on training performance and proposing the network optimization strategies to enhance the noise immunity of OCNN. Specifically, the noise immunity is improved by adjusting the pooling method and pooling size, and the Dropout regularization is introduced after the pooling layer to further enhance the model's recognition accuracy. Experimental results indicate that the proposed on-chip training scheme effectively mitigates errors caused by the fabrication inaccuracy in the photonic devices. However, the circuit noise remains the primary factor limiting the OCNN performance. Notably, under the high circuit noise conditions, e.g. when the standard deviation of MZI phase error caused by circuit noise reaches 0.003, the combination of maximum pooling and Dropout regularization significantly improves the recognition accuracy of OCNN, which achieves a maximum of 78%. This research provides valuable insights for implementing on-chip training in OCNNs and explores new approaches for deploying hybrid optical-electronic architectures in high-noise environments.
-
Key words:
- OCNN /
- on-chip training /
- Mach-Zehnder Interferometer
-
图 1 (a) OCNN架构示意图，(b) OCNN的片上训练实施图
Figure 1. (a) Schematic diagram of the OCNN architecture, (b) Implementation diagram of on-chip training for OCNN
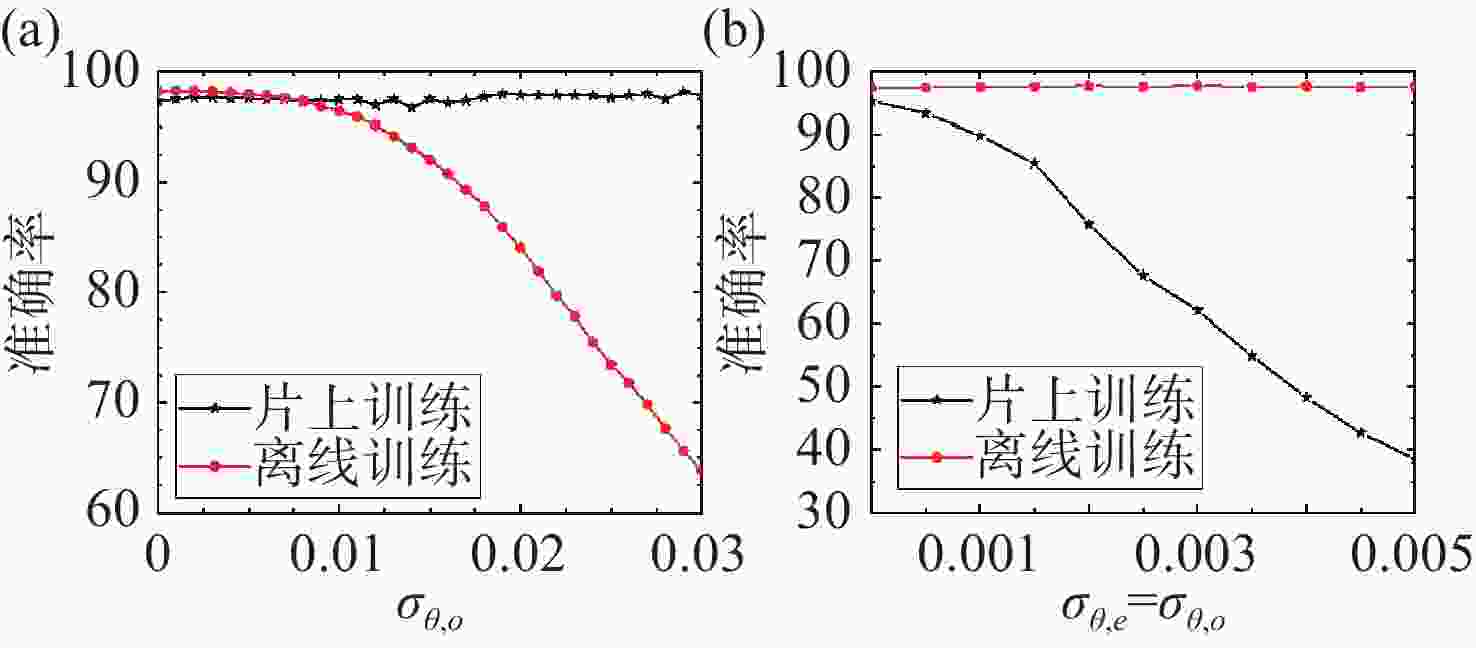
图 3 (a)仅有制备误差时，OCNN离线训练与片上训练的识别准确率；(b)在制备误差与电路噪声共同存在时，OCNN离线训练与片上训练的识别准确率
Figure 3. (a) Recognition accuracies of OCNN under offline and on-chip training, with fabrication error only, (b) recognition accuracies of OCNN under offline and on-chip training, with both fabrication error and circuit noise
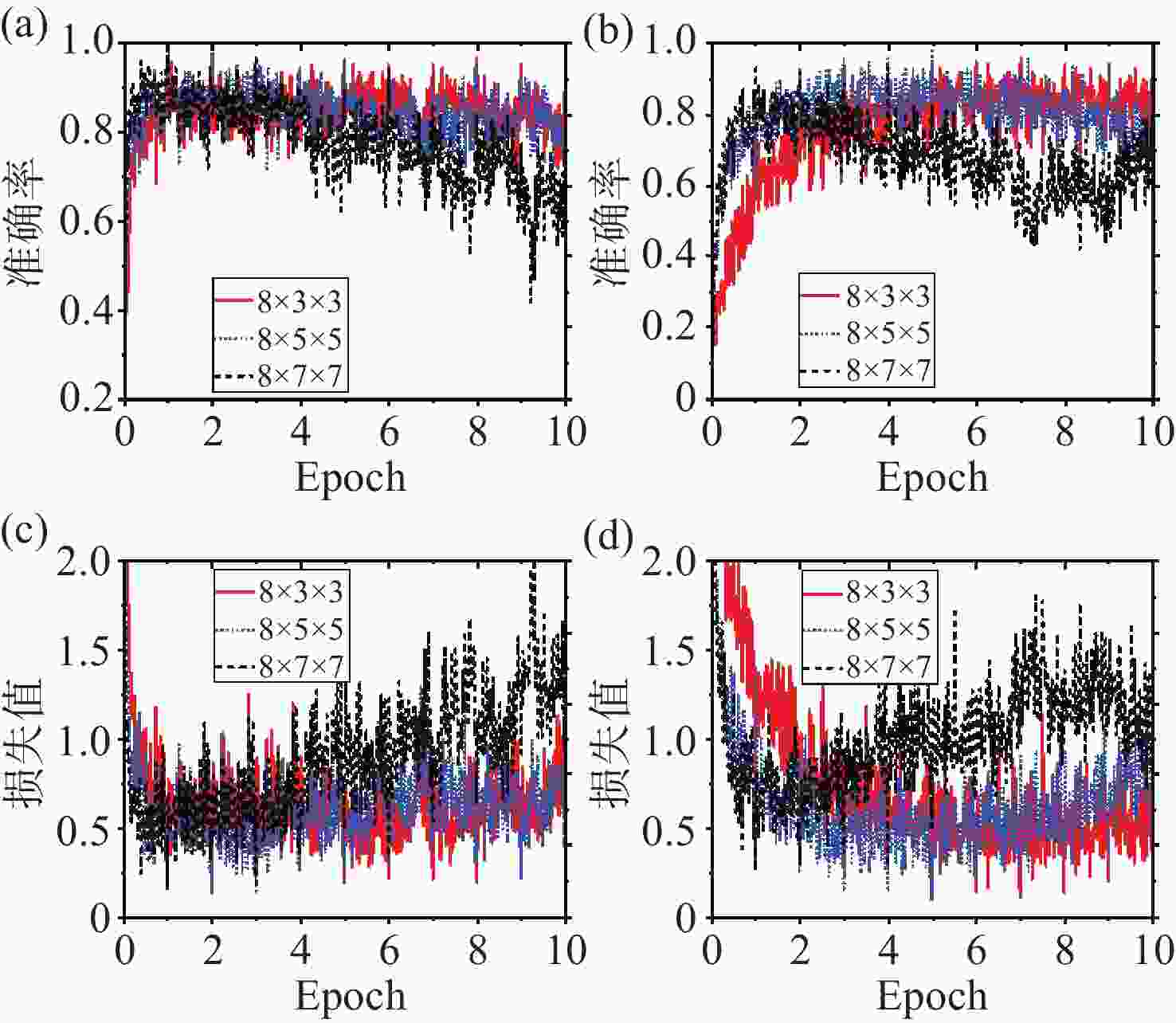
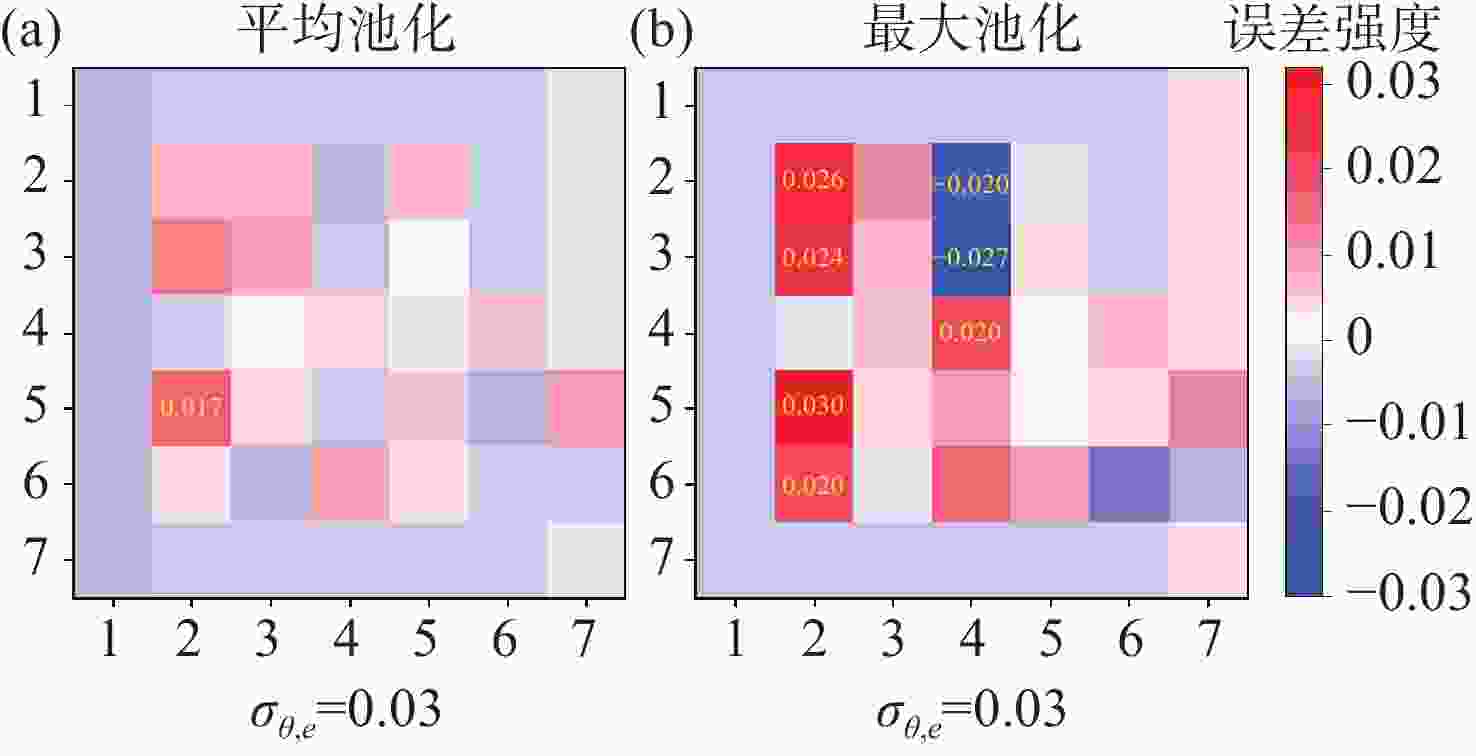
图 4 在电路噪声σθ,e=0.003时，(a)和(b)是不同池化尺寸的平均池化和最大池化方式下OCNN的识别准确率，(c)和(d)是相应情况下的损失值。
Figure 4. When the circuit noise σθ,e =0.003, (a) and (b) show the recognition accuracies of OCNN under average pooling and maximum pooling methods with different pooling sizes, (c) and (d) show the corresponding loss values.
图 5 (a)平均池化和(b)最大池化后特征图的差值热力图
Figure 5. Difference heatmaps of the feature map after (a) average pooling and (b) maximum pooling.
图 6 在3×3特征图上Dropout正则化结果的示例(p = 0.5)
Figure 6. Example of Dropout regularization results on a 3×3 feature map (p = 0.5).
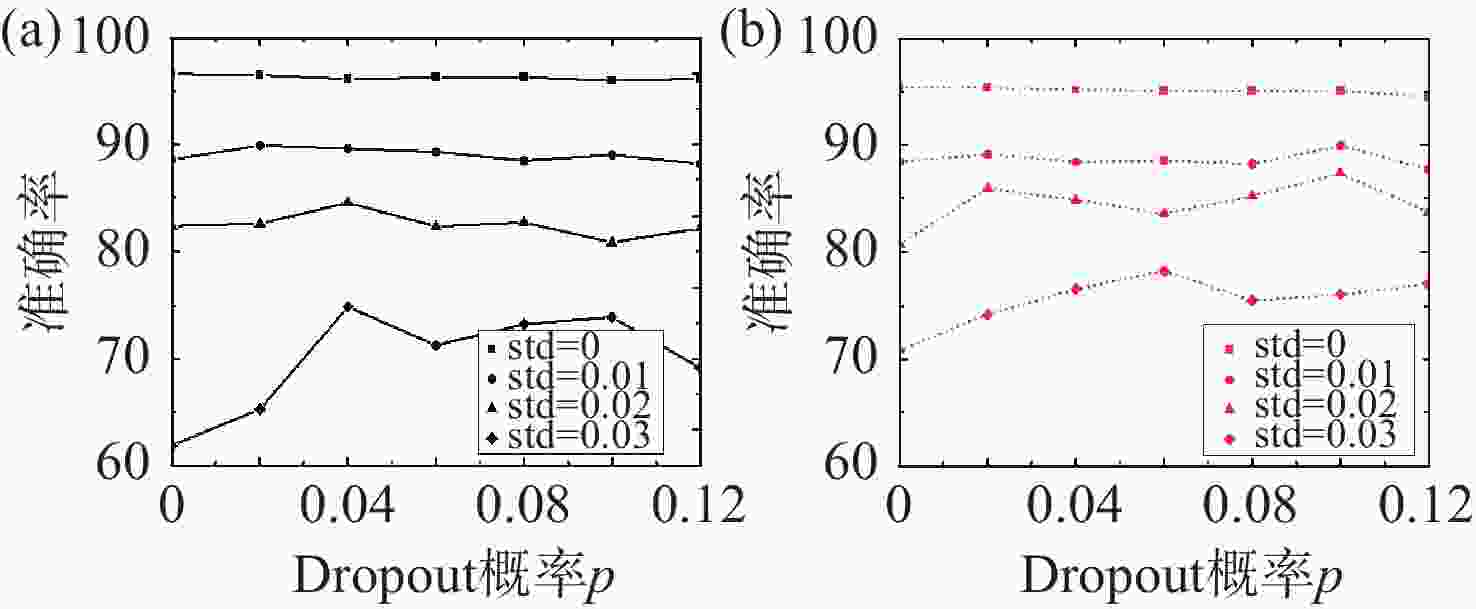
图 7 (a)平均池化和(b)最大池化方式下OCNN在不同Dropout概率p时的识别精确度，其中图例是电路噪声标准差σθ,e，分别为0、0.001、0.002、0.003
Figure 7. Recognition accuracies of OCNN under different dropout probabilities p with (a) average pooling, and (b) with max pooling, where the legends are the standard deviation of circuit noise σθ,e of 0, 0.001, 0.002, and 0.003 respectively.
表 1 OCNN的模型参数
Table 1. Model Parameters of OCNN
功能层 滤波器尺寸 输入尺寸 输出尺寸 卷积层
(等宽填充)8@3×3 28×28×1 28×28×8 池化层 N×N 28×28×8 $ \dfrac{{28}}{N} \times \dfrac{{28}}{N} \times 8 $ 全连接层 $ \dfrac{{28}}{N} \times \dfrac{{28}}{N} \times 8 $ $ \dfrac{{28}}{N} \times \dfrac{{28}}{N} \times 8 $ 10 
下载: 导出CSV
表 2 采用不同池化方式和尺寸的OCNN的识别准确率
Table 2. The recognition accuracy of OCNN with different pooling methods and sizes.
测试准确率(%) 池化后特征图尺寸 8·7·7 8·5·5 8·3·3 平均池化 39.36 68.52 63.84 最大池化 52.80 64.01 72.27
下载: 导出CSV
-
[1] ZHAO X, WANG L M, ZHANG Y F, et al. A review of convolutional neural networks in computer vision[J]. Artificial Intelligence Review, 2024, 57(4): 99. doi: 10.1007/s10462-024-10721-6 [2] SUN Y N, XUE B, ZHANG M J, et al. Evolving deep convolutional neural networks for image classification[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 394-407. doi: 10.1109/TEVC.2019.2916183 [3] WALDROP M M. More than moore[J]. Nature, 2016, 530(7589): 144-148. (查阅网上资料, 未找到本条文献期号信息, 请确认). [4] WANG Y. Neural networks on chip: From CMOS accelerators to in-memory-computing[C]. Proceedings of 2018 31st IEEE International System-on-Chip Conference (SOCC), IEEE, 2018: 1-3. [5] FU T ZH, ZHANG J F, SUN R, et al. Optical neural networks: progress and challenges[J]. Light: Science & Applications, 2024, 13(1): 263. [6] FELDMANN J, YOUNGBLOOD N, WRIGHT C D, et al. All-optical spiking neurosynaptic networks with self-learning capabilities[J]. Nature, 2019, 569(7755): 208-214. doi: 10.1038/s41586-019-1157-8 [7] GU L X, ZHANG L F, NI R H, et al. Giant optical nonlinearity of Fermi polarons in atomically thin semiconductors[J]. Nature Photonics, 2024, 18(8): 816-822. doi: 10.1038/s41566-024-01434-x [8] ASHTIANI F, ON M B, SANCHEZ-JACOME D, et al. Photonic max-pooling for deep neural networks using a programmable photonic platform[C]. Proceedings of 2023 Optical Fiber Communications Conference and Exhibition (OFC), IEEE, 2023: 1-3. [9] SHAO X F, SU J Y, LU M H, et al. All-optical convolutional neural network with on-chip integrable optical average pooling for image classification[J]. Applied Optics, 2024, 63(23): 6263-6271. doi: 10.1364/AO.524502 [10] YU Y Z, CAO Y, WANG G, et al. Optical diffractive convolutional neural networks implemented in an all-optical way[J]. Sensors, 2023, 23(12): 5749. doi: 10.3390/s23125749 [11] XU SH F, WANG J, WANG R, et al. High-accuracy optical convolution unit architecture for convolutional neural networks by cascaded acousto-optical modulator arrays[J]. Optics Express, 2019, 27(14): 19778-19787. doi: 10.1364/OE.27.019778 [12] CHENG Y, ZHANG J N, ZHOU T K, et al. Photonic neuromorphic architecture for tens-of-task lifelong learning[J]. Light: Science & Applications, 2024, 13(1): 56. [13] QI J, WANG SH, LIU ZH, et al. A gradient-free training approach for optical neural networks based on stochastic functions[J]. Proceedings of SPIE, 2024, 13236: 132360R. [14] GU J, ZHU H, FENG C, et al. L2ight: enabling on-chip learning for optical neural networks via efficient in-situ subspace optimization[C]. Proceedings of the 35th International Conference on Neural Information Processing Systems, Curran Associates Inc. , 2021: 662. [15] FANG M Y S, MANIPATRUNI S, WIERZYNSKI C, et al. Design of optical neural networks with component imprecisions[J]. Optics Express, 2019, 27(10): 14009-14029. doi: 10.1364/OE.27.014009 [16] SHOKRANEH F, GEOFFROY-GAGNON S, LIBOIRON-LADOUCEUR O. The diamond mesh, a phase-error- and loss-tolerant field-programmable MZI-based optical processor for optical neural networks[J]. Optics Express, 2020, 28(16): 23495-23508. doi: 10.1364/OE.395441 [17] MOJAVER K H R, ZHAO B K, LEUNG E, et al. Addressing the programming challenges of practical interferometric mesh based optical processors[J]. Optics Express, 2023, 31(15): 23851-23866. doi: 10.1364/OE.489493 [18] TSAI Y H, HAMSICI O C, YANG M H. Adaptive region pooling for object detection[C]. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2015: 731-739. [19] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958. [20] CLEMENTS W R, HUMPHREYS P C, METCALF B J, et al. Optimal design for universal multiport interferometers[J]. Optica, 2016, 3(12): 1460-1465. doi: 10.1364/OPTICA.3.001460 [21] MITTAL S. A survey of FPGA-based accelerators for convolutional neural networks[J]. Neural Computing and Applications, 2020, 32(4): 1109-1139. doi: 10.1007/s00521-018-3761-1 [22] HAMERLY R, BANDYOPADHYAY S, ENGLUND D. Asymptotically fault-tolerant programmable photonics[J]. Nature Communications, 2022, 13(1): 6831. doi: 10.1038/s41467-022-34308-3 [23] SALEHIN I, KANG D K. A review on dropout regularization approaches for deep neural networks within the scholarly domain[J]. Electronics, 2023, 12(14): 3106. doi: 10.3390/electronics12143106 [24] GHOLAMALINEZHAD H, KHOSRAVI H. Pooling methods in deep neural networks, a review[J]. arxiv preprint arxiv:, 2009, 07485: 2020. (查阅网上资料, 不确定本条文献类型与格式, 请确认). [25] SALEHIN I, KANG D K. A review on dropout regularization approaches for deep neural networks within the scholarly domain[J]. Electronics, 2023, 12(14): 3106. (查阅网上资料, 本条文献与第23条文献重复, 请确认). [26] JU Y G. Scalable optical convolutional neural networks based on free-space optics using lens arrays and a spatial light modulator[J]. Journal of Imaging, 2023, 9(11): 241. doi: 10.3390/jimaging9110241 [27] HE K M, ZHANG X Y, REN SH Q, et al. Deep residual learning for image recognition[C]. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2016: 770-778. [28] PEARL N, TREIBITZ T, KORMAN S. NAN: Noise-aware NeRFs for burst-denoising[C]. Proceedings of 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, IEEE, 2022: 12662-12671. [29] XIE J, LIU S Y, CHEN J X, et al. Huber loss based distributed robust learning algorithm for random vector functional-link network[J]. Artificial Intelligence Review, 2023, 56(8): 8197-8218. doi: 10.1007/s10462-022-10362-7 -
下载:
计量
- 文章访问数: 81
- HTML全文浏览量: 18
- PDF下载量: 5
- 被引次数: 0
