一种双永磁同步电机滑模同步驱动控制方法

宋晓莉; 张驰; 郭亚伟

doi:10.37188/CO.EN-2022-0026

一种双永磁同步电机滑模同步驱动控制方法

宋晓莉^{1, 2, ,},
张驰^{1, 2, 3},
郭亚伟^{1, 2, 3}

1.
中国科学院国家天文台南京天文光学技术研究所, 南京210042
2.
中国科学院天文光学技术重点实验室(南京天文光学技术研究所), 南京210042
3.
中国科学院大学，北京100049

详细信息

中图分类号: TP273
计量
- 文章访问数: 183
- HTML全文浏览量: 123
- PDF下载量: 121
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-23
- 修回日期: 2022-12-23
- 录用日期: 2023-01-30
- 网络出版日期: 2023-06-06

A sliding-mode control of a Dual-PMSMs synchronization driving method

doi: 10.37188/CO.EN-2022-0026

SONG Xiao-li^{1, 2
, ,},
ZHANG Chi^{1, 2, 3},
GUO Ya-wei^{1, 2, 3}

1.
National Astronomical Observatories/Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences, Nanjing 210042, China
2.
CAS Key Laboratory of Astronomical Optics & Technology, Nanjing Institute of Astronomical Optics & Technology, Nanjing 210042, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: Supported by National Natural Science Foundation of China (No. 11673045); Joint Found of National Natural Science of China (No. U2031147)

More Information

Author Bio:
Song Xiao-Li (1978—), female, born in Henan Province. She received her Ph.D. degree in astrophysics from the Graduate University of Chinese Academy of Sciences, China, in 2012. She won the Excellent Award of the President of the Chinese Academy of Sciences in 2012. She received her B.S. and M.S. degrees in Power Electronics and Power Drive from Anhui University of Science & Technology, China in 2001 and 2004, respectively. From 2012 to 2015, she was an assistant research fellow with the Telescope New Technology Laboratory, National Astronomical Observatories/Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences. Since 2016, she has been an associate research fellow with the Telescope New Technology Laboratory, National Astronomical Observatories/Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences. Her research interests focus on the driving & control of the axes control systems of large-aperture telescopes and the multi-motor driving and control of dynamic systems. She has published numerous papers in journals and international conferences, applied for and received several patents, and presided over and participated in many projects for the National Natural Science Foundation of China related to the above topics. E-mail: xlsong@niaot.ac.cn

Corresponding author: xlsong@niaot.ac.cn

摘要

摘要:
速度同步性能和抗干扰性是影响双永磁同步电机（dual-PMSM）同步运行动态响应和稳态精度的重要因素。通过引入交叉耦合控制作为模型，提出了一种基于改进双功率趋近律的积分滑模速度跟踪控制器，以减小两台电机之间的速度误差。设计了负载转矩观测器，将观测值引入滑模控制（SMC）趋近律，以提高系统的抗干扰性能。同时，采用模糊比例积分微分（FPID）控制设计了同步控制器，以提高双永磁同步电机的同步性。验证结果表明，当目标转速为800 r/min时，与传统的PI算法相比，所提出的控制方法可以在空载启动时将两台电机的速度同步误差从25 r/min降低到12 r/min，在负载突然转矩下将速度同步误差由7 r/min降低至2.2 r/min，从而提高了同步性和抗干扰性。
- 滑模控制 /
- 交叉耦合控制 /
- 改进双幂次趋近律 /
- 观测器 /
- 双永磁同步电机
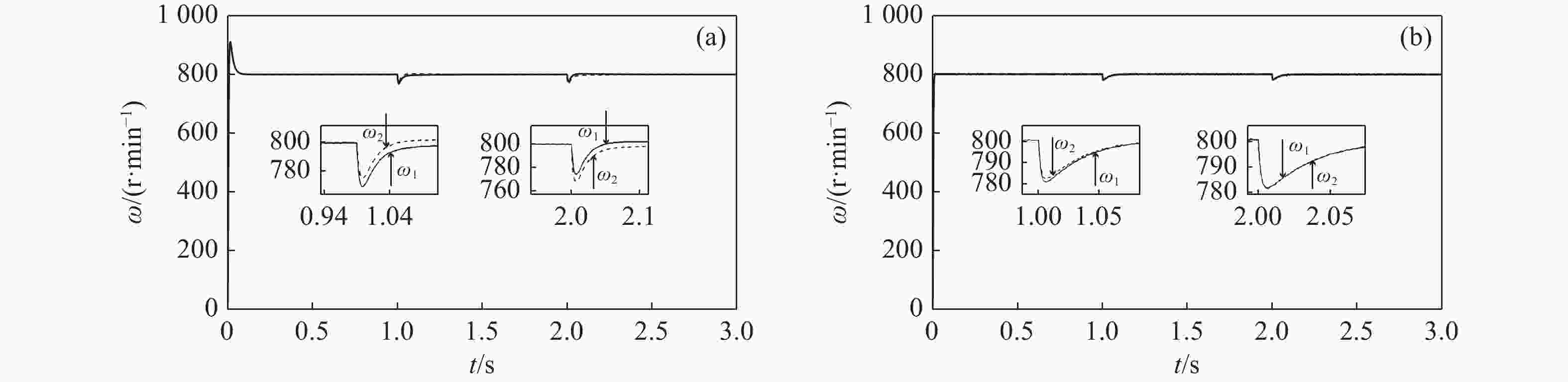
Abstract:
Speed synchronization performance and anti-interference are important factors that affect the synchronous operation dynamic response and steady-state accuracy of dual Permanent Magnet Synchronous Motors’ (Dual-PMSMs). By introducing cross-coupling control as the framework, an integral sliding mode speed tracking controller based on an improved bi-power reaching method is proposed to reduce the speed error between two motors. A load torque observer is designed to bring the observed value into the Sliding Mode Control (SMC) reaching method that enhances the anti-disturbance performance of the system. Meanwhile, a synchronous controller is designed using a Fuzzy-Proportional-Integral-Derivative (FPID) control to improve the synchronization of the Dual-PMSMs. The results show that compared with the traditional PI algorithm as the target speed is 800 r/min, the proposed control method can decrease the two motors’ speed synchronization error from 25 r/min to 12 r/min under a no-load startup and reduce the speed synchronization error from 7 r/min to 2.2 r/min with sudden load torque, improving the synchronization and disturbance rejection.
- sliding mode control /
- cross-coupling control /
- improved bi-power reaching method /
- observer /
- Dual-PMSMs

HTML全文

Figure 1. Block diagram of the speed controller

下载: 全尺寸图片幻灯片

Figure 2. Structural block diagram of the disturbance torque observer

下载: 全尺寸图片幻灯片

Figure 3. Surface diagram of ∆k_p value output

下载: 全尺寸图片幻灯片

Figure 4. Surface diagram of ∆k_i value output

下载: 全尺寸图片幻灯片

Figure 5. Overall block diagram of dual-motor synchronous control system

下载: 全尺寸图片幻灯片

Figure 6. Comparison of speed response waveforms between the improved and traditional reaching methods

下载: 全尺寸图片幻灯片

Figure 7. Speed waveforms obtained by different methods under no-load torque starting condition. (a) Conventional cross-coupled control. (b) Improved bi-power reaching method

下载: 全尺寸图片幻灯片

Figure 8. Synchronization error waveforms obtained by different methods under no-load torque startup condition. (a) Conventional cross-coupling control. (b) Improved bi-power reaching method sliding mode control

下载: 全尺寸图片幻灯片

Figure 9. Torque speed waveforms obtained by different methods under sudden load torque condition. (a) Conventional cross-coupling control. (b) Improved bi-power reaching method sliding mode control

下载: 全尺寸图片幻灯片

Figure 10. Synchronization error waveforms obtained by different methods under sudden surge load torque condition. (a) Conventional cross-coupling control. (b) Improved bi-power reaching method sliding mode control

下载: 全尺寸图片幻灯片

Table 2. k_i fuzzy rule table

∆$\omega_c $	∆$\omega $
∆$\omega_c $	NB	NM	NS	ZE	PS	PM	PB
NB	NB	NB	NB	NM	NS	ZE	ZE
NM	NB	NB	NM	NS	NS	ZE	PS
NS	NB	NM	NS	NS	ZE	PS	PM
ZE	NM	NM	NS	ZE	PS	PM	PM
PS	NM	NM	NS	ZE	PS	PS	PB
PM	ZE	ZE	PS	PS	PM	PB	PB
PB	ZE	ZE	PS	PM	PM	PB	PB

下载: 导出CSV

Table 1. k_p fuzzy rule table

∆$\omega_c $	∆$\omega $
∆$\omega_c $	NB	NM	NS	ZE	PS	PM	PB
NB	PB	PB	PB	PM	PS	ZE	ZE
NM	PB	PB	PM	PM	ZE	ZE	NS
NS	PB	PM	PM	PS	ZE	NS	NS
ZE	PM	PM	PS	ZE	NS	NM	NM
PS	PM	PS	ZE	NS	NS	NM	NM
PM	PS	ZE	NS	NM	NM	NM	NB
PB	ZE	ZE	NM	NM	NB	NB	NB

下载: 导出CSV

Table 3. Parameters of the motor

Parameters	PMSM1	PMSM2
R(Ω)	7.29	12.24
L(mH)	0.14	0.18
P	4	4
J (kg∙m²)	0.000945	0.000885
ω_N (r/min)	1500	1500
T_N (N∙m)	2	2.5
B(N∙m∙s)	0.0090577	0.0080581

下载: 导出CSV

Table 4. SMC controller parameters

	k₁	k₂	k₃	c	α	β	η
PMSM1	5	3	50	0.2	0.13	2	0.0001
PMSM2	5	3	1200	0.35	0.13	2	0.0001

下载: 导出CSV

参考文献(22)

[1]	ZHANG X Y, SHI T N, WANG ZH Q, et al. Generalized predictive contour control of the biaxial motion system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8488-8497. doi: 10.1109/TIE.2018.2808899
[2]	JUNG J W, LEU V Q, DO T D, et al. Adaptive PID speed control design for permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 900-908. doi: 10.1109/TPEL.2014.2311462
[3]	WU Y J, CHENG Y B, WANG Y L. Research on a multi-motor coordinated control strategy based on fuzzy ring network control[J]. IEEE Access, 2020, 8: 39375-39388. doi: 10.1109/ACCESS.2020.2974906
[4]	LU Y K. Adaptive-fuzzy control compensation design for direct adaptive fuzzy control[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(6): 3222-3231. doi: 10.1109/TFUZZ.2018.2815552
[5]	HU X L, SUN CH Y, ZHANG B. Design of recurrent neural networks for solving constrained least absolute deviation problems[J]. IEEE Transactions on Neural Networks, 2010, 21(7): 1073-1086. doi: 10.1109/TNN.2010.2048123
[6]	LIANG D L, LI J, QU R H, et al. Adaptive second-order sliding-mode observer for PMSM sensorless control considering VSI nonlinearity[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8994-9004. doi: 10.1109/TPEL.2017.2783920
[7]	ZENG T Y, REN X M, ZHANG Y. Fixed-time sliding mode control and high-gain nonlinearity compensation for dual-motor driving system[J]. IEEE Transactions on Industrial Informatics, 2020, 16(6): 4090-4098. doi: 10.1109/TII.2019.2950806
[8]	ZHANG X G, SUN L ZH, ZHAO K, et al. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1358-1365. doi: 10.1109/TPEL.2012.2206610
[9]	RODRIGUEZ J, KAZMIERKOWSKI M P, ESPINOZA J R, et al. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1003-1016. doi: 10.1109/TII.2012.2221469
[10]	KARAMANAKOS P, GEYER T. Guidelines for the design of finite control set model predictive controllers[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7434-7450. doi: 10.1109/TPEL.2019.2954357
[11]	WANG H, SHI L H, MAN ZH H, et al. Continuous fast nonsingular terminal sliding mode control of automotive electronic throttle systems using finite-time exact observer[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7160-7172. doi: 10.1109/TIE.2018.2795591
[12]	LI SH H, ZHOU M M, YU X H. Design and implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 1879-1891. doi: 10.1109/TII.2012.2226896
[13]	LI J, FANG Y T, HUANG X Y, et al. Comparison of synchronization control techniques for traction motors of high-speed trains[C]. Proceedings of the 17th International Conference on Electrical Machines and Systems, IEEE, 2014: 2l14-2119.
[14]	KOREN Y. Cross-coupled biaxial computer control for manufacturing systems[J]. Journal of Dynamic Systems, Measurement, and Control, 1980, 102(4): 265-272. doi: 10.1115/1.3149612
[15]	SHIH Y T, CHEN CH SH, LEE A CH. A novel cross-coupling control design for Bi-axis motion[J]. International Journal of Machine Tools and Manufacture, 2002, 42(14): 1539-1548. doi: 10.1016/S0890-6955(02)00109-8
[16]	SHI T N, LIU H, GENG Q, et al. Improved relative coupling control structure for multi-motor speed synchronous driving system[J]. IET Electric Power Applications, 2016, 10(6): 451-457. doi: 10.1049/iet-epa.2015.0515
[17]	LIM CH SH, LEVI E, JONES M, et al. A comparative study of synchronous current control schemes based on FCS-MPC and PI-PWM for a two-motor three-phase drive[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8): 3867-3878. doi: 10.1109/TIE.2013.2286573
[18]	BRANDO G, PIEGARI L, SPINA I. Simplified optimum control method for monoinverter dual parallel PMSM drive[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3763-3771. doi: 10.1109/TIE.2017.2758751
[19]	XU B, SHEN X K, JI W, et al. Adaptive nonsingular terminal sliding model control for permanent magnet synchronous motor based on disturbance observer[J]. IEEE Access, 2018, 6: 48913-48920. doi: 10.1109/ACCESS.2018.2867463
[20]	ZHOU X L, LI X F. Trajectory tracking control for electro-optical tracking system using ESO based fractional- order sliding mode control[J]. IEEE Access, 2021, 9: 45891-45902. doi: 10.1109/ACCESS.2021.3067680
[21]	GAO W B, HUNG J C. Variable structure control of nonlinear systems: a new approach[J]. IEEE Transactions on Industrial Electronics, 1993, 40(1): 45-55. doi: 10.1109/41.184820
[22]	BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766. doi: 10.1137/S0363012997321358