Controllable inversion and focusing behaviors of Swallowtail-Gaussian beams in fractional Schrödinger equations
doi: 10.37188/CO.EN-2023-0018
-
摘要:
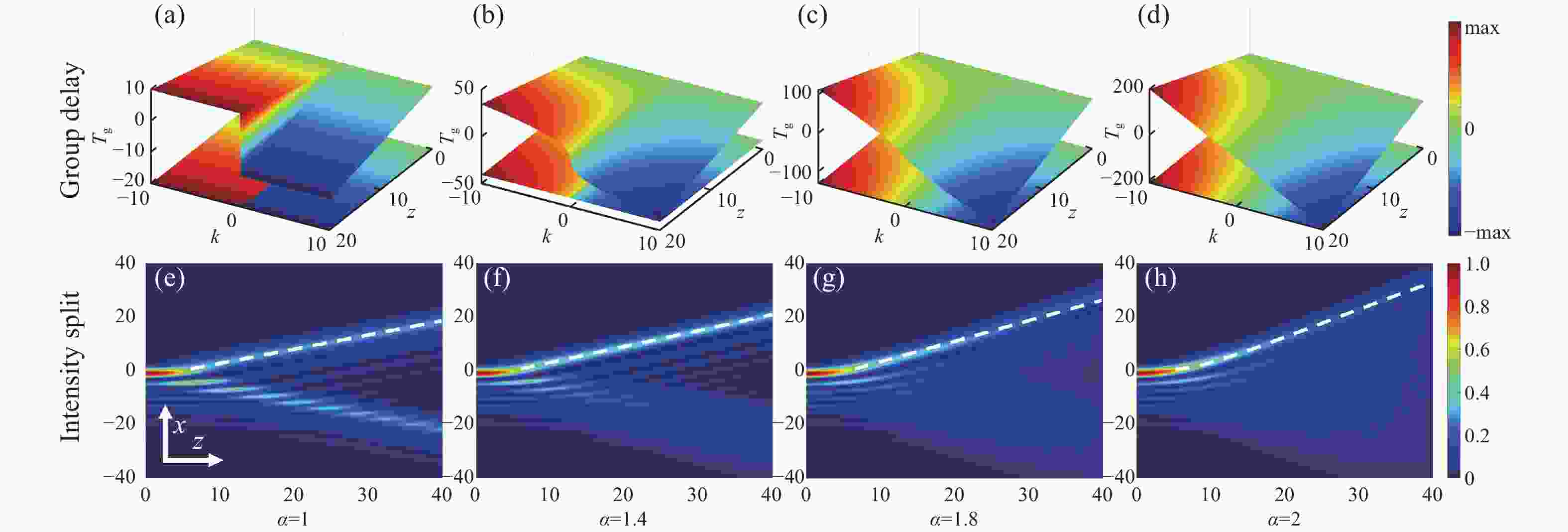
在光场中引入一维燕尾突变函数,利用分步傅立叶方法研究了燕尾高斯(SG)光束在分数薛定谔方程(FSE)中的演化动力学,详细讨论了线性势、抛物线势、高斯势及无势的情况。在无势情况下,SG光束会因群延迟的变化而分裂成两个子光束,并且分裂轨迹会随着Lévy指数的增大出现弯曲。在线性势下,SG光束出现了周期性反转和聚焦行为,Lévy指数和线性势系数分别影响聚焦点峰值强度和反转及聚焦的演化周期,其反转和聚焦周期距离只受线性势影响而与Lévy指数无关。在抛物线势情况下,具有较大Lévy指数的SG光束的主瓣和旁瓣反转和聚焦从杂乱转变为周期性演化,其反转聚焦位置由抛物线势系数和Lévy指数共同决定。在高斯势中,光束的演化在势垒的约束下由于反射主瓣和旁瓣的干扰,窄势垒的周期性反转和聚焦出现杂乱混沌现象,而对于宽势垒,由于旁瓣减弱,周期性演化变得清晰。本文研究结果为利用高阶燕尾光波场实现光调制器和光开关提供了可能。
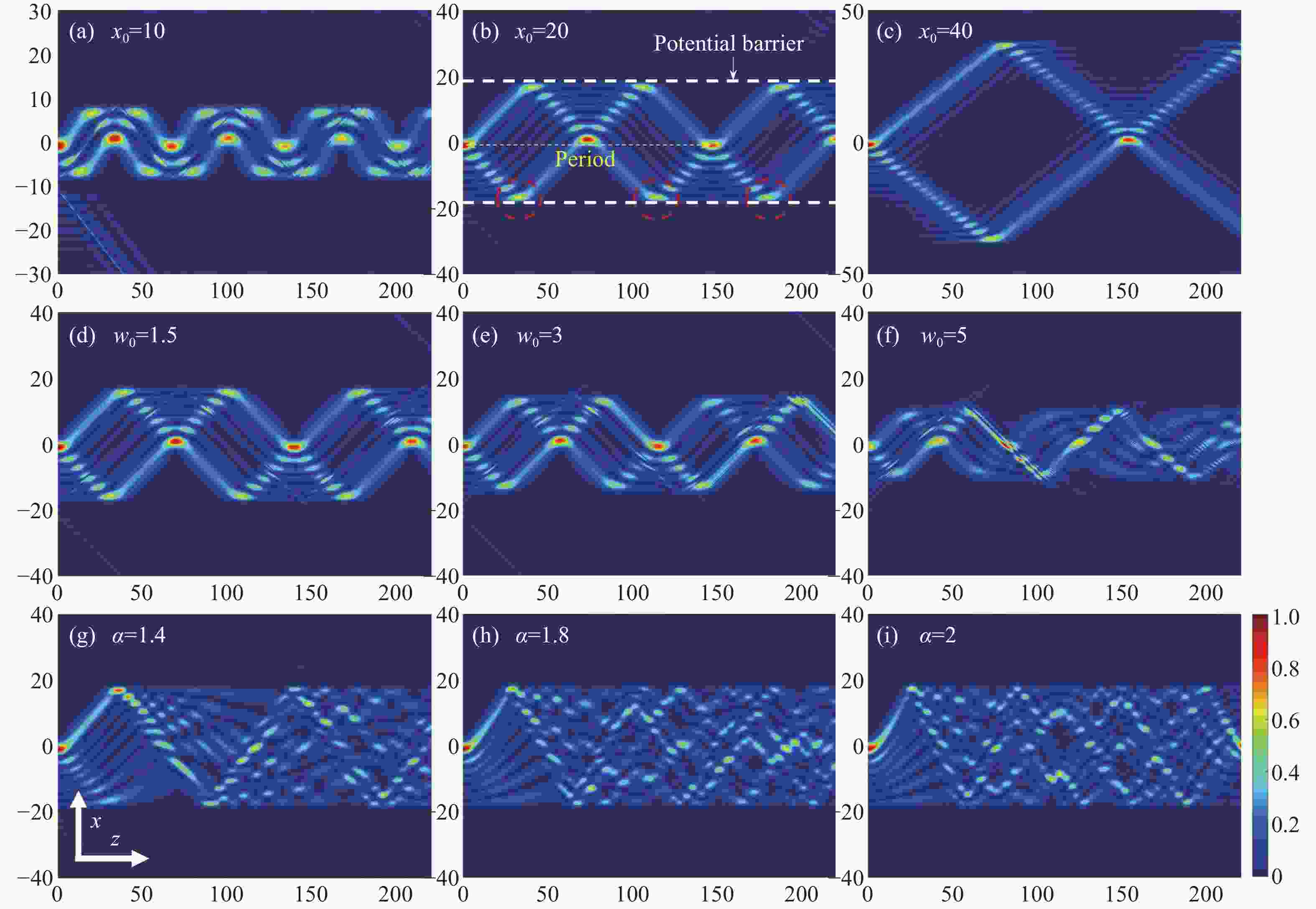
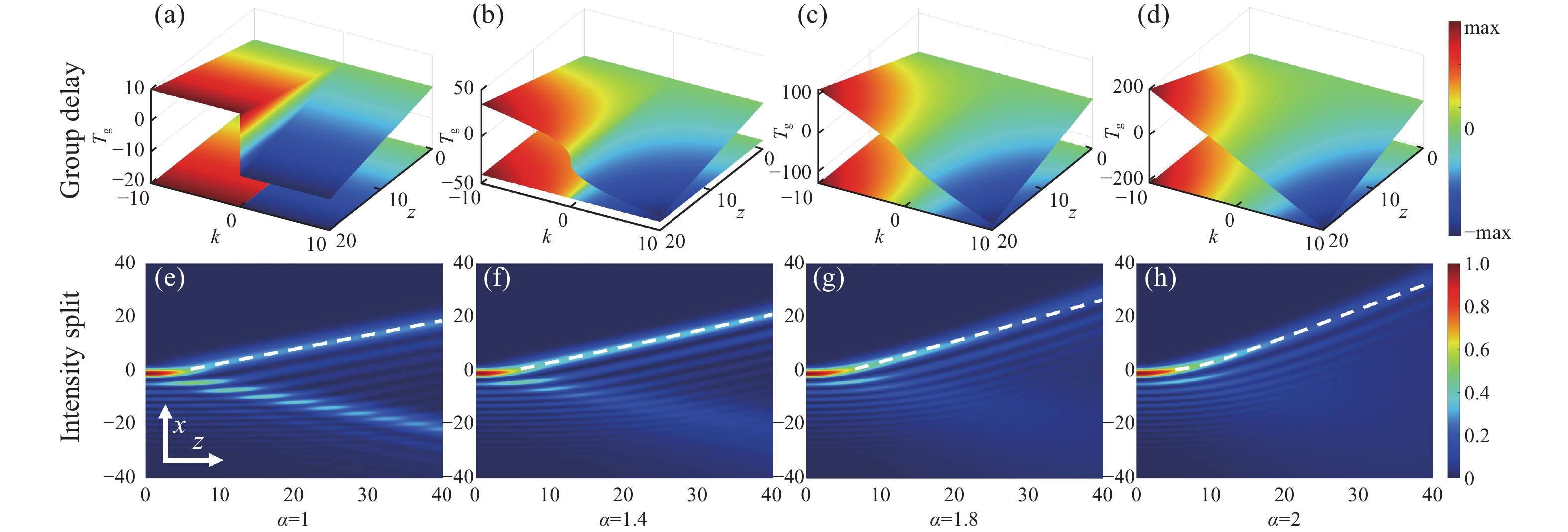
Abstract:By transferring a one-dimensional swallowtail catastrophe to an optical field, the evolution dynamics of the Swallowtail-Gaussian (SG) beams in fractional Schrödinger equations (FSE) with different potentials, which include the linear, parabolic, and Gaussian potential and non-potential cases, were investigated using the split-step Fourier method. In a non-potential case, the SG beams split into two sub-beams, and their splitting trajectories along straight lines can be curved with a larger Lévy index in FSE. In a linear potential case, periodic inversion and focusing behaviors are found, and a larger Lévy index can strengthen their peak intensities at focusing points and curve trajectories. However, the period distance of inversion and focusing is only affected by linear potentials rather than the Lévy index. In a parabolic potential case, the beams evolve from chaos interference into an apparent period in inversion and focusing of main and side lobes with a larger Lévy index, where the inversion and focusing position are combined and determined by parabolic potential and the Lévy index. In a Gaussian potential case, the evolution dynamics are evidently constrained within potential barriers. In a narrow barrier, the periodic inversion and focusing display chaotic behavior because of the interference of both the reflected main and side lobes. In contrast, the periodic evolution in a wider barrier becomes more prominent owing to the attenuation of the side lobes. The study of the SG beam in FSE offers the possibility of optical modulators and switches through the utilization of the higher-order swallowtail catastrophe wave fields.
-
Key words:
- Swallowtail-Gaussian beam /
- Fractional Schrödinger equation /
- Lévy index
-
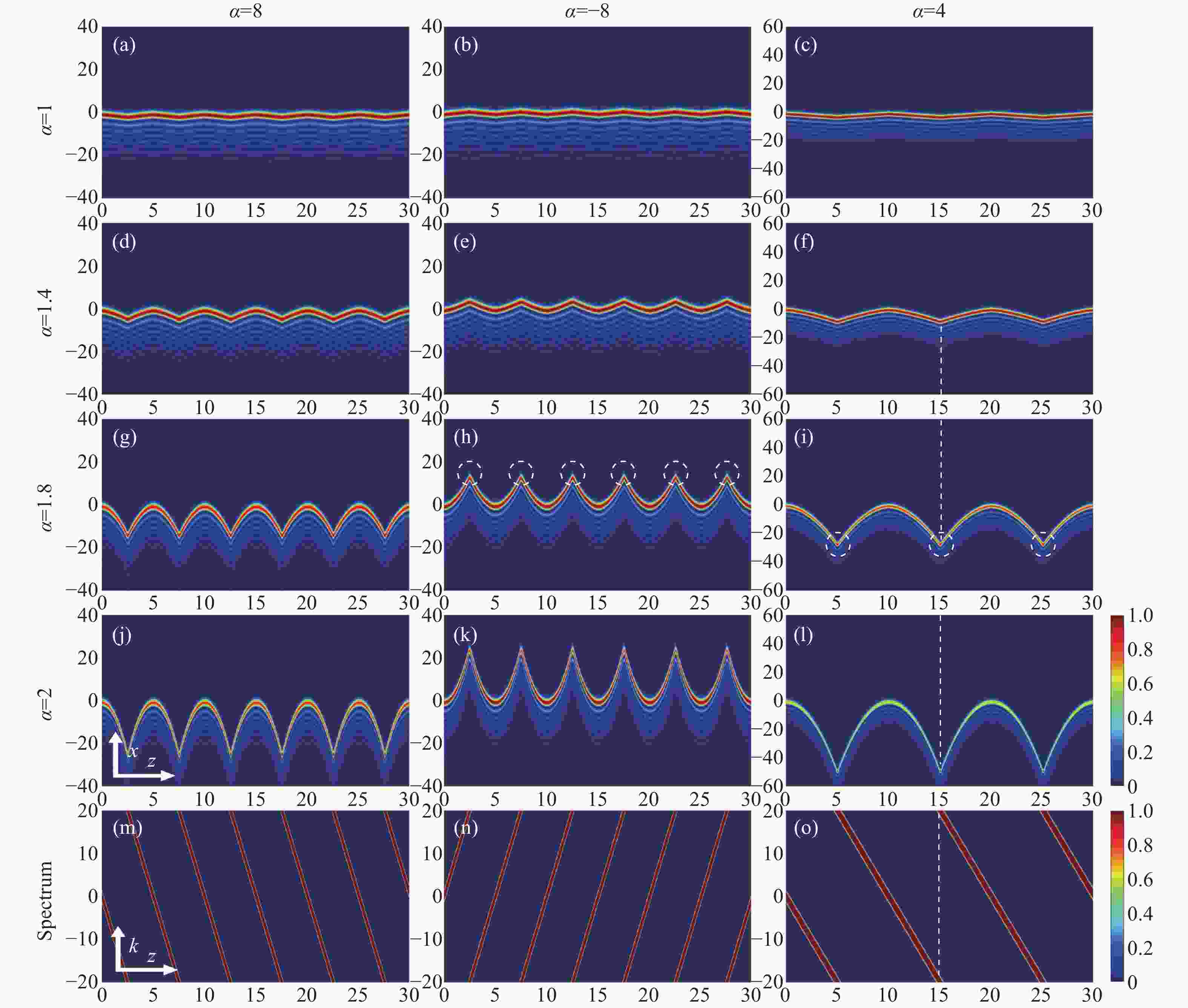
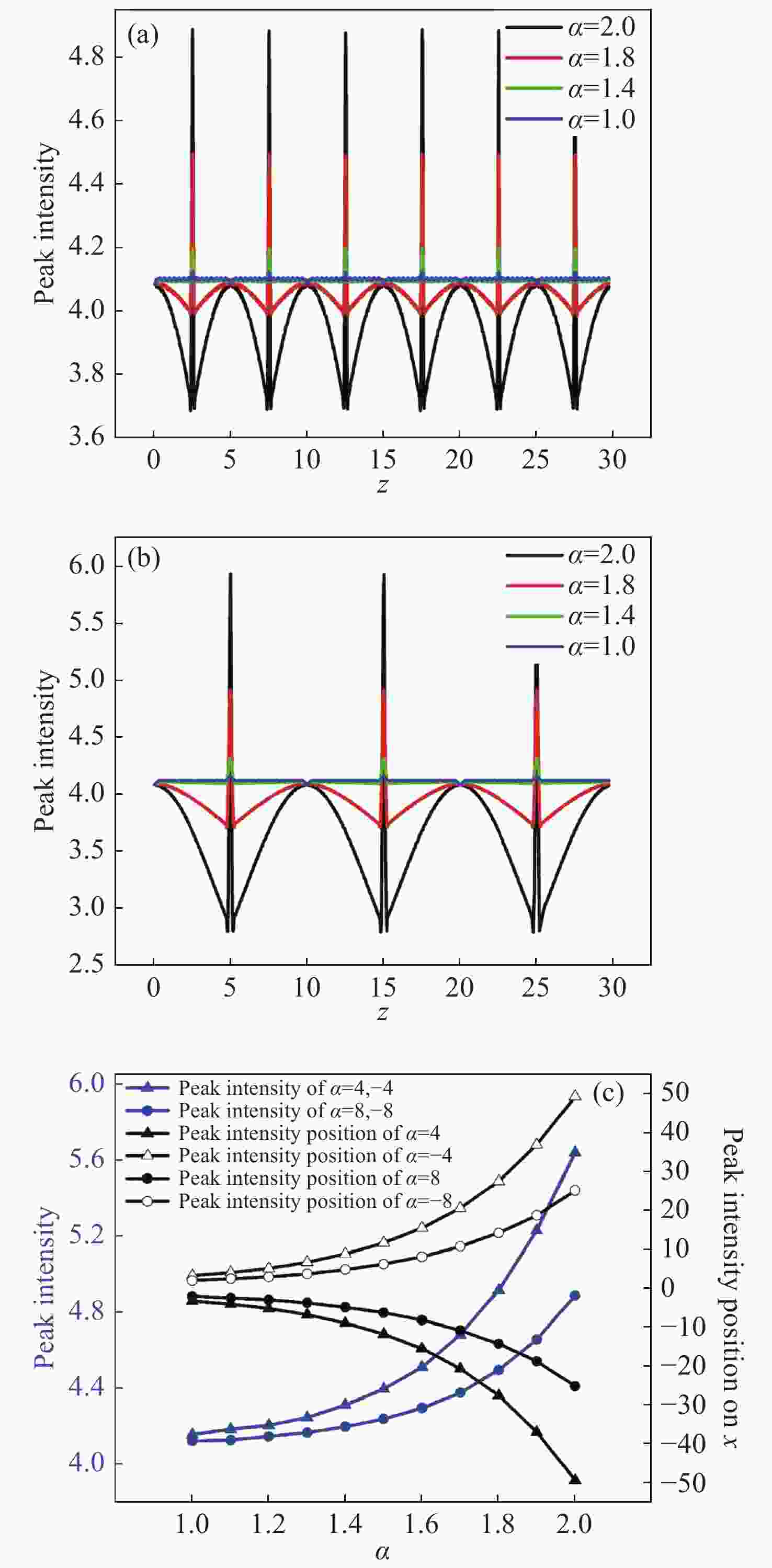
Figure 3. Peak intensities and their positions of SG beams with a linear potential for different Lévy indexes α and linear potential coefficients a during propagation. (a) a = 8, (b) a = 4, (c) the peak intensity (Max) of the longitudinal coordinate in transmission varies with the change of the Lévy indexes α(a = −4, +4, −8, +8)
-
[1] KIRK N P, CONNOR J N L, CURTIS P R, et al. Theory of axially symmetric cusped focusing: numerical evaluation of a Bessoid integral by an adaptive contour algorithm[J]. Journal of Physics A:Mathematical and General, 2000, 33(26): 4797-4808. doi: 10.1088/0305-4470/33/26/306 [2] BERRY M V, UPSTILL C. IV catastrophe optics: morphologies of caustics and their diffraction patterns[J]. Progress in Optics, 1980, 18: 257-346. [3] SIVILOGLOU G A, CHRISTODOULIDES D N. Accelerating finite energy Airy beams[J]. Optics Letters, 2007, 32(8): 979-981. doi: 10.1364/OL.32.000979 [4] RING J D, LINDBERG J, MOURKA A, et al. Auto-focusing and self-healing of Pearcey beams[J]. Optics Express, 2012, 20(17): 18955-18966. doi: 10.1364/OE.20.018955 [5] CHEN ZH G, MORANDOTTI R. Nonlinear Photonics and Novel Optical Phenomena[M]. New York: Springer, 2012. [6] ZANNOTTI A, DIEBEL F, DENZ C. Dynamics of the optical swallowtail catastrophe[J]. Optica, 2017, 4(10): 1157-1162. doi: 10.1364/OPTICA.4.001157 [7] ZANNOTTI A, DIEBEL F, BOGUSLAWSKI M, et al. Optical catastrophes of the swallowtail and butterfly beams[J]. New Journal of Physics, 2017, 19(5): 053004. doi: 10.1088/1367-2630/aa6ecd [8] CHENG K, LU G, ZHONG X Q. The Poynting vector and angular momentum density of Swallowtail-Gauss beams[J]. Optics Communications, 2017, 396: 58-65. doi: 10.1016/j.optcom.2017.03.038 [9] CHENG K, LU G, ZHOU Y, et al. The Poynting vector and angular momentum density of the autofocusing Butterfly-Gauss beams[J]. Optics & Laser Technology, 2018, 105: 23-34. [10] CHENG K, LIANG M T, SHU L Y, et al. Polarization states and Stokes vortices of dual Butterfly-Gauss vortex beams with uniform polarization in uniaxial crystals[J]. Optics Communications, 2022, 504: 127471. doi: 10.1016/j.optcom.2021.127471 [11] TENG H A, QIAN Y X, LAN Y P, et al. Abruptly autofocusing circular swallowtail beams[J]. Optics Letters, 2021, 46(2): 270-273. doi: 10.1364/OL.415709 [12] TENG H A, QIAN Y X, LAN Y P. Swallowtail-type diffraction catastrophe beams[J]. Optics Express, 2021, 29(3): 3786-3794. doi: 10.1364/OE.416134 [13] TENG H A, HU J T, CAI Y M, et al. Caustics and wavefront of Swallowtail-Gauss catastrophe beams[J]. Results in Physics, 2022, 42: 105991. doi: 10.1016/j.rinp.2022.105991 [14] JIANG J J, XU D L, MO ZH W, et al. Generation and control of tornado waves by means of ring swallowtail vortex beams[J]. Optics Express, 2022, 30(7): 11331-11344. doi: 10.1364/OE.453165 [15] ZHANG N CH, SONG J Q, LI D M, et al. Multi-focus autofocusing circular hyperbolic umbilic beams[J]. Optics Express, 2022, 30(18): 32978-32989. doi: 10.1364/OE.467601 [16] LASKIN N. Fractional Schrödinger equation[J]. Physical Review E, 2002, 66(5): 056108. doi: 10.1103/PhysRevE.66.056108 [17] LONGHI S. Fractional Schrödinger equation in optics[J]. Optics Letters, 2015, 40(6): 1117-1120. doi: 10.1364/OL.40.001117 [18] ZANG F, WANG Y, LI L. Dynamics of Gaussian beam modeled by fractional Schrödinger equation with a variable coefficient[J]. Optics Express, 2018, 26(18): 23740-23750. doi: 10.1364/OE.26.023740 [19] ZHANG Y Q, LIU X, BELIĆ M R, et al. Propagation dynamics of a light beam in a fractional Schrödinger equation[J]. Physical Review Letters, 2015, 115(18): 180403. doi: 10.1103/PhysRevLett.115.180403 [20] ZHANG Y Q, BELIĆ M R, ZHANG L, et al. Periodic inversion and phase transition of finite energy Airy beams in a medium with parabolic potential[J]. Optics Express, 2015, 23(8): 10467-10480. doi: 10.1364/OE.23.010467 [21] ZHANG Y Q, LIU X, BELIĆ M R, et al. Automatic Fourier transform and self-Fourier beams due to parabolic potential[J]. Annals of Physics, 2015, 363: 305-315. doi: 10.1016/j.aop.2015.10.006 [22] ZHANG Y Q, LIU X, BELIĆ M R, et al. Anharmonic propagation of two-dimensional beams carrying orbital angular momentum in a harmonic potential[J]. Optics Letters, 2015, 40(16): 3786-3789. doi: 10.1364/OL.40.003786 [23] ZENG L W, ZENG J H. Preventing critical collapse of higher-order solitons by tailoring unconventional optical diffraction and nonlinearities[J]. Communications Physics, 2020, 3(1): 26. doi: 10.1038/s42005-020-0291-9 [24] LI L, LI H G, RUAN W, et al. Gap solitons in parity-time-symmetric lattices with fractional-order diffraction[J]. Journal of the Optical Society of America B, 2020, 37(2): 488-494. doi: 10.1364/JOSAB.376975 [25] CHE W W, YANG F W, CAO SH L, et al. Gray solitons in parity-time-symmetric localized potentials with fractional-order diffraction[J]. Physics Letters A, 2021, 413: 127606. doi: 10.1016/j.physleta.2021.127606 [26] MALOMED B A. Optical solitons and vortices in fractional media: a mini-review of recent results[J]. Photonics, 2021, 8(9): 353. doi: 10.3390/photonics8090353 [27] LIU X Y, MALOMED B A, ZENG J H. Localized modes in nonlinear fractional systems with deep lattices[J]. Advanced Theory and Simulations, 2022, 5(4): 2100482. doi: 10.1002/adts.202100482 [28] ZHONG M, YAN ZH Y. Spontaneous symmetry breaking and ghost states in two-dimensional fractional nonlinear media with non-Hermitian potential[J]. Communications Physics, 2023, 6(1): 92. doi: 10.1038/s42005-023-01212-1 [29] XU CH J, WU J H, WU Y, et al. Propagation of the Pearcey Gaussian beams in a medium with a parabolic refractive index[J]. Optics Communications, 2020, 464: 125478. doi: 10.1016/j.optcom.2020.125478 [30] LIN Z J, XU C J, HUANG H Q, et al. Accelerating trajectory manipulation of symmetric Pearcey Gaussian beam in a uniformly moving parabolic potential[J]. Optics Express, 2021, 29(11): 16270-16283. doi: 10.1364/OE.424489 [31] GAO R, GUO T, REN SH M, et al. Periodic evolution of the Pearcey-Gaussian beam in the fractional Schrödinger equation under Gaussian potential[J]. Journal of Physics B: Atomic, Molecular and Optical Physics, 2022, 55(9): 095401. [32] GAO R, REN SH M, GUO T, et al. Propagation dynamics of chirped Pearcey-Gaussian beam in fractional Schrödinger equation under Gaussian potential[J]. Optik, 2022, 254: 168661. doi: 10.1016/j.ijleo.2022.168661 [33] ZHANG X, ZHANG J, CHEN CH SH, et al. Controllable focusing behavior of chirped Pearcey-Gaussian pulses under time-dependent potentials[J]. Optics Express, 2022, 30(19): 34835-34847. doi: 10.1364/OE.471329 [34] LIU SH L, ZHANG Y W, MALOMED B A, et al. Experimental realisations of the fractional Schrödinger equation in the temporal domain[J]. Nature Communications, 2023, 14(1): 222. doi: 10.1038/s41467-023-35892-8 [35] HUANG X W, SHI X H, DENG ZH X, et al. Potential barrier-induced dynamics of finite energy Airy beams in fractional Schrödinger equation[J]. Optics Express, 2017, 25(26): 32560-32569. doi: 10.1364/OE.25.032560 [36] HUANG X W, DENG ZH X, FU X Q. Dynamics of finite energy Airy beams modeled by the fractional Schrödinger equation with a linear potential[J]. Journal of the Optical Society of America B, 2017, 34(5): 976-982. doi: 10.1364/JOSAB.34.000976 -





 下载:
下载: