Electromagnetic Bloch-like oscillations in Fibonacci metamaterial waveguide arrays
doi: 10.37188/CO.EN-2024-0033
-
摘要:
本文研究了一种特异材料构成的波导阵列中光传输的类布洛赫振荡特性，这种准周期波导阵列是由金属和介质两种介质按斐波那契数列的顺序排列组成。通过研究高斯脉冲在结构中传输时的广场分布，可以直观地观察其光场演化情况。在没有引入厚度梯度或介电常数梯度情形下，在第九代斐波那契准周期波导中发现了三种振荡模式。另外，随着入射脉冲波长的增加，在第九代和第十代斐波那契准周期波导中类布洛赫振荡周期产生红移，这为布洛赫振荡调控提供了一种有意义的途径。
Abstract:This paper investigates optical transport in metamaterial waveguide arrays (MMWAs) exhibiting Bloch-like oscillations (BLOs). The MMWAs is fabricated by laterally combining metal and dielectric layers in a Fibonacci sequence. By mapping the field distribution of Gaussian wave packets in these arrays, we directly visualize the mechanical evolution in a classical wave environment. Three distinct oscillation modes are observed at different incident positions in the ninth-generation Fibonacci structure, without introducing thickness or refractive index gradient in any layer. Additionally, the propagation period of BLOs increases with a redshift of the incident wavelength for both ninth- and tenth-generation Fibonacci MMWAs. These findings provide a valuable method for manipulating BLOs and offer new insights into optical transport in metamaterials, with potential applications in optical device and wave control technologies.
-
Key words:
- quasiperiodic /
- Bloch-like oscillation /
- metamaterial /
- Fibonacci
-
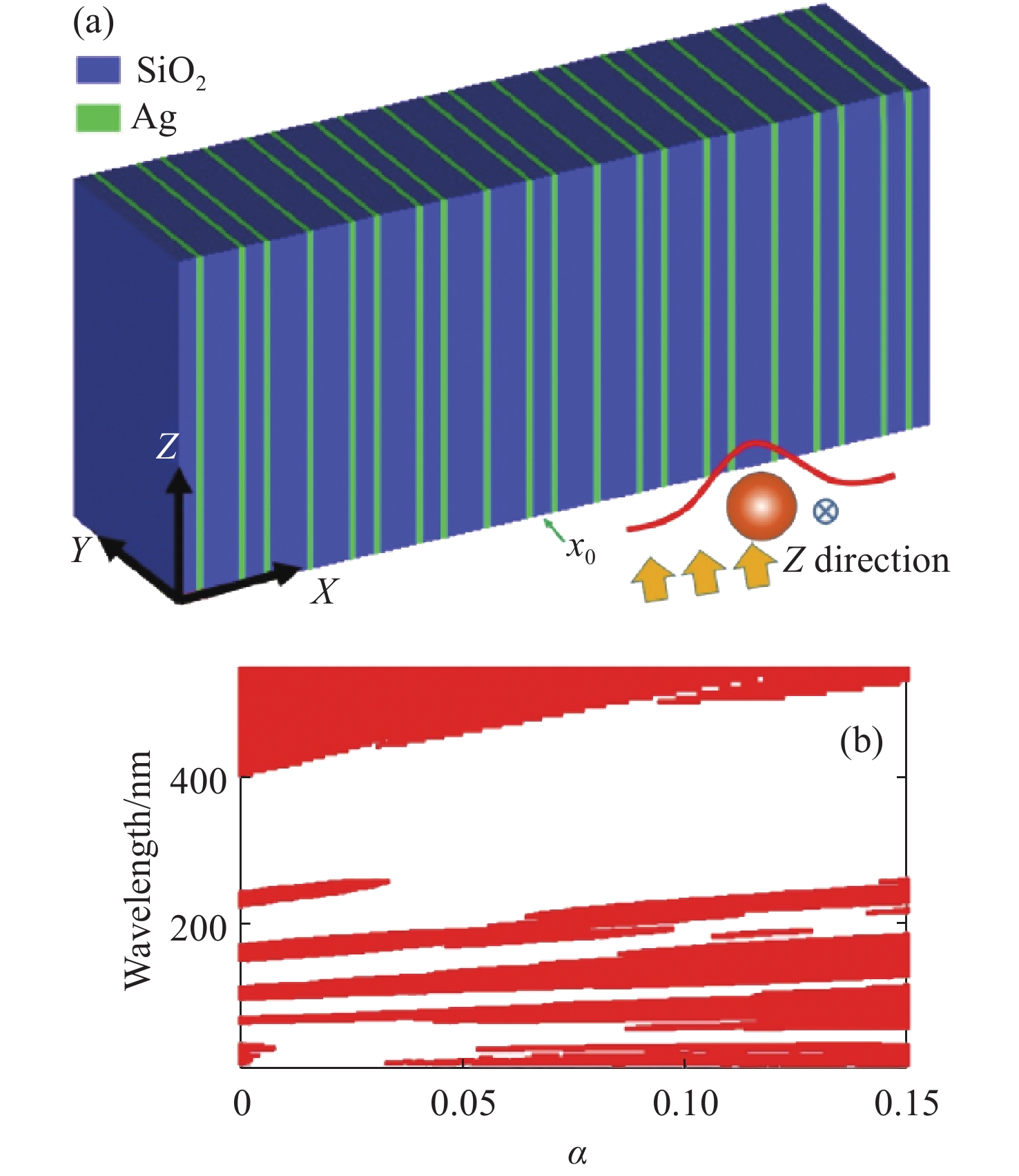
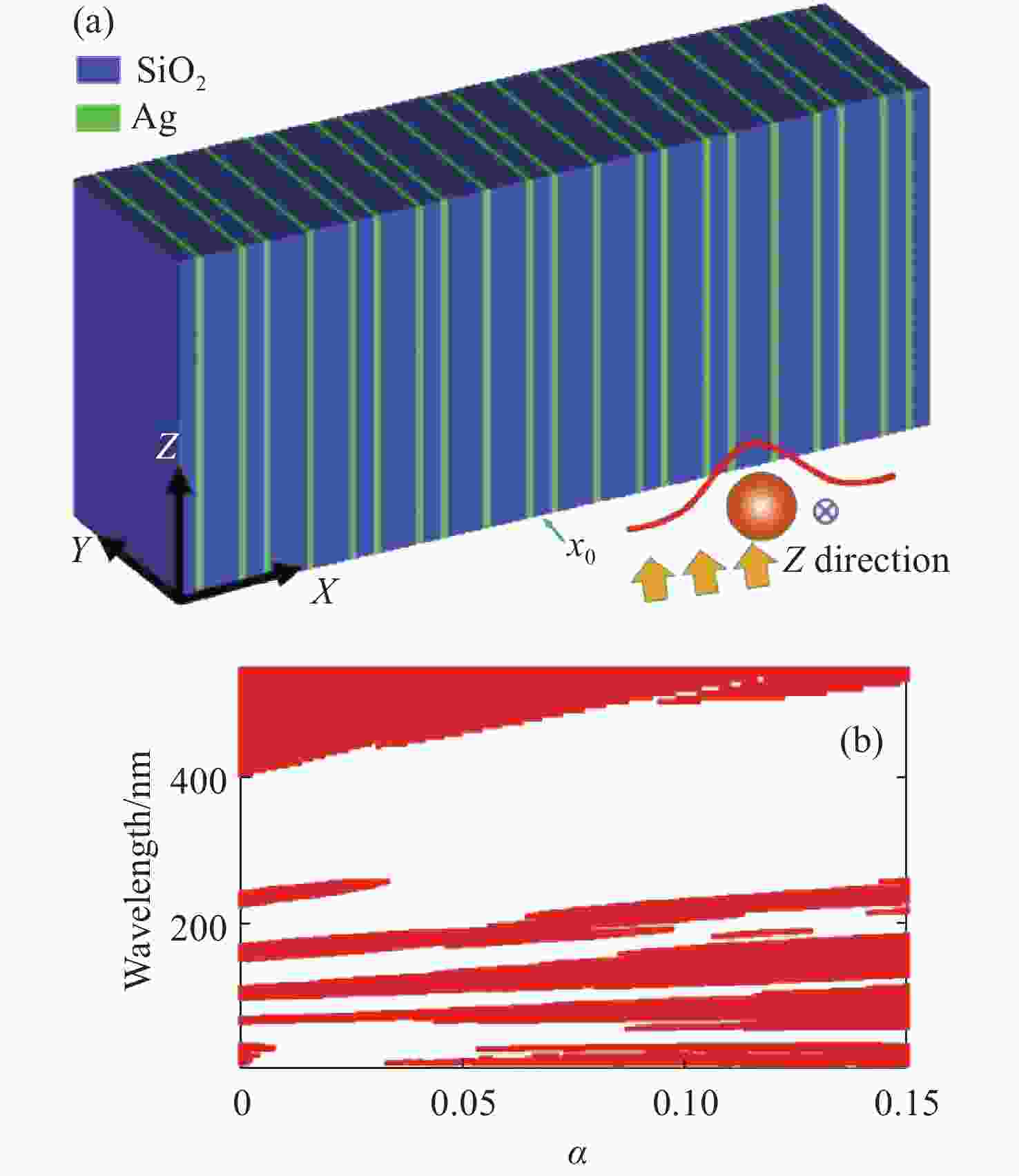
Figure 1. (Color online) (a) Schematic illustration of the 2D quasiperiodic waveguide array. The blue and green layers represent the silicon dioxide dielectric layer and the silver layer, respectively. The electromagnetic waves are incident along the Y-direction. The amplitude of the Gaussian pulse is shown in the red line. And the circle shows the intensity distribution. (b) The band diagram of the graded MMWA with a gradient
$ {\alpha _{}} $ increasing from 0 to 0.15 for the dielectric permittivity with a relation of$ {\varepsilon _a} = {\varepsilon _0} + \alpha (N - 1) $ . Red regions represent the minigaps, white regions represent the minibands.
Figure 2. (Color online) (a) and (b) show contours of magnetic field intensity
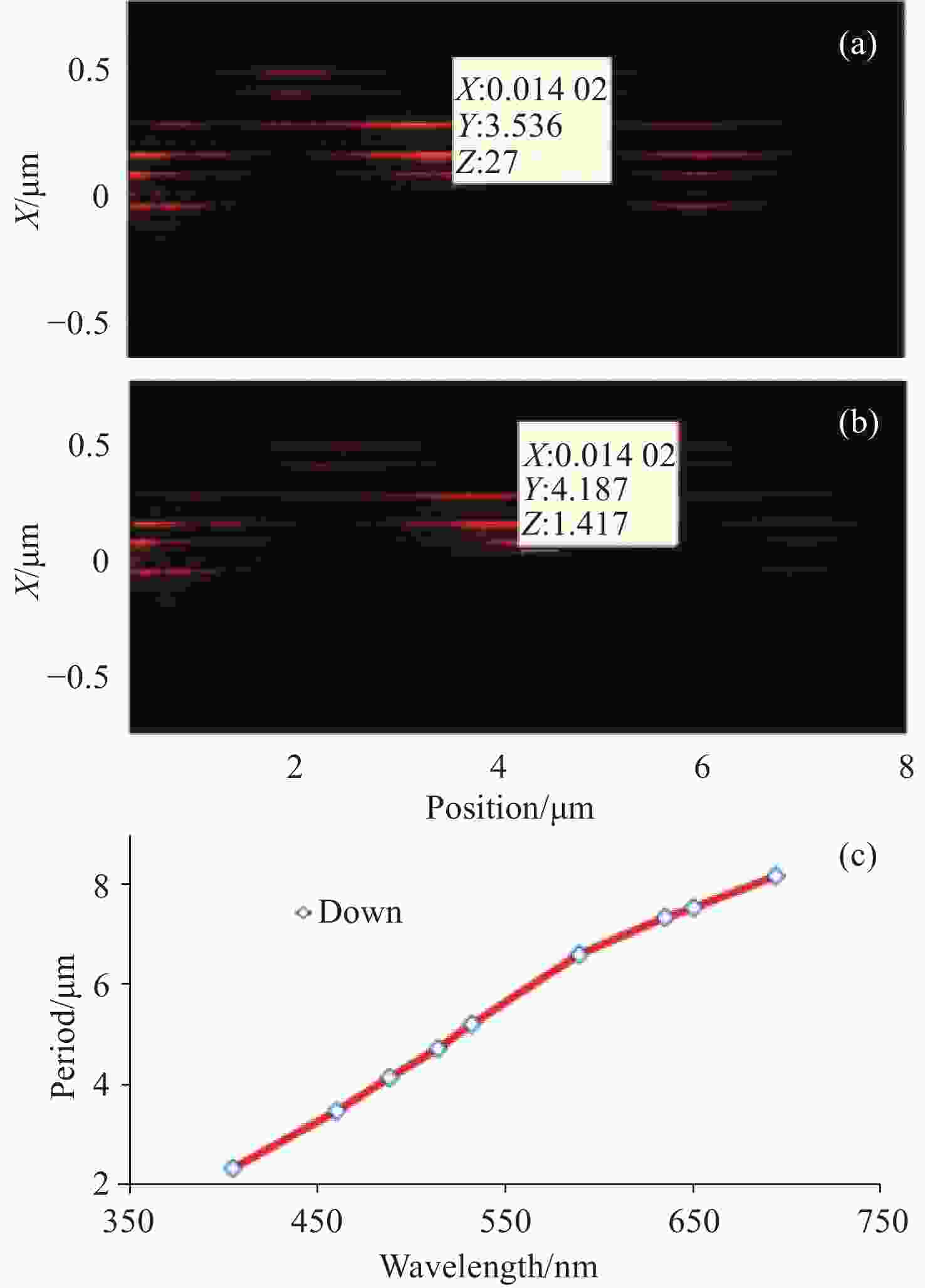
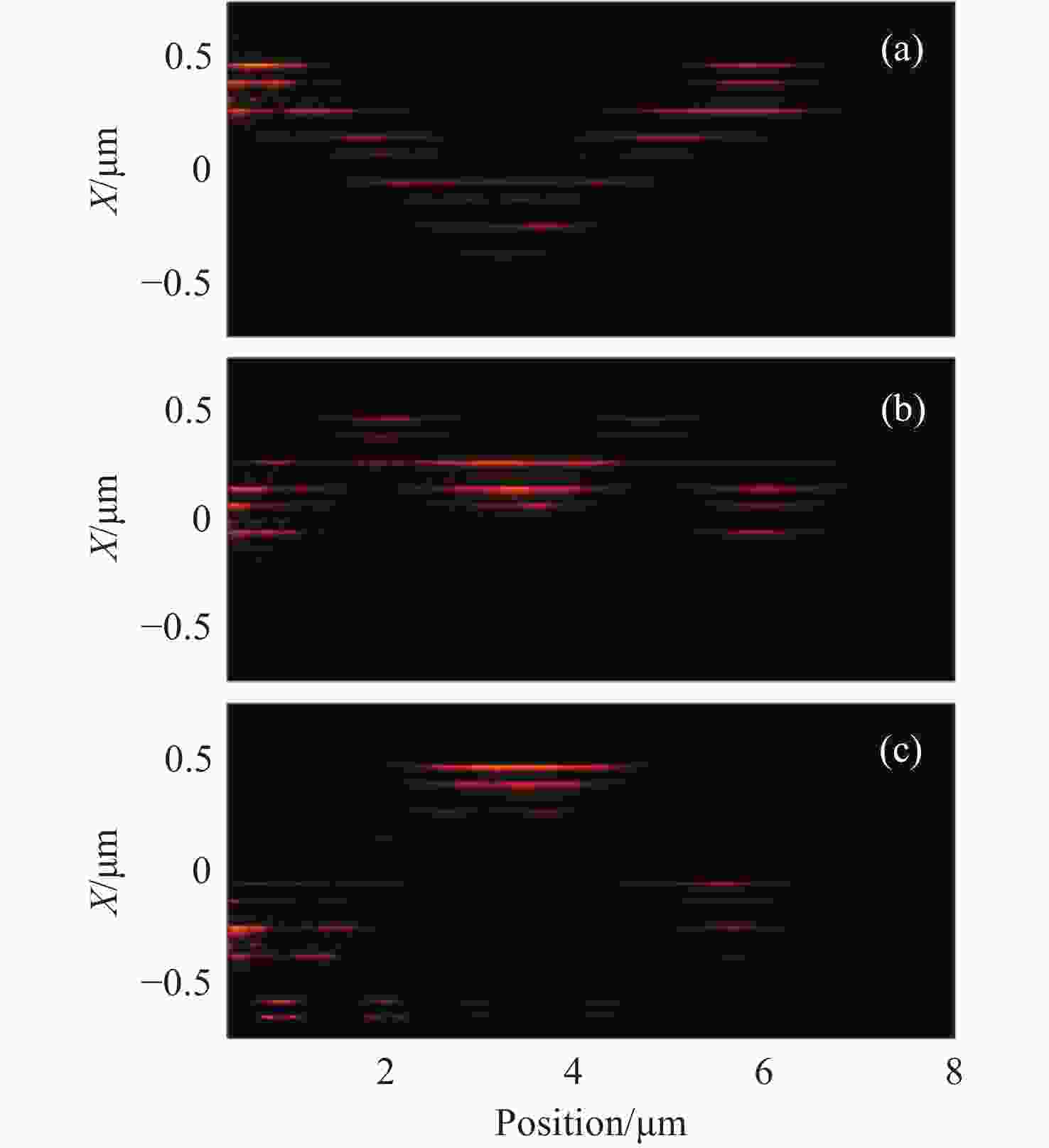
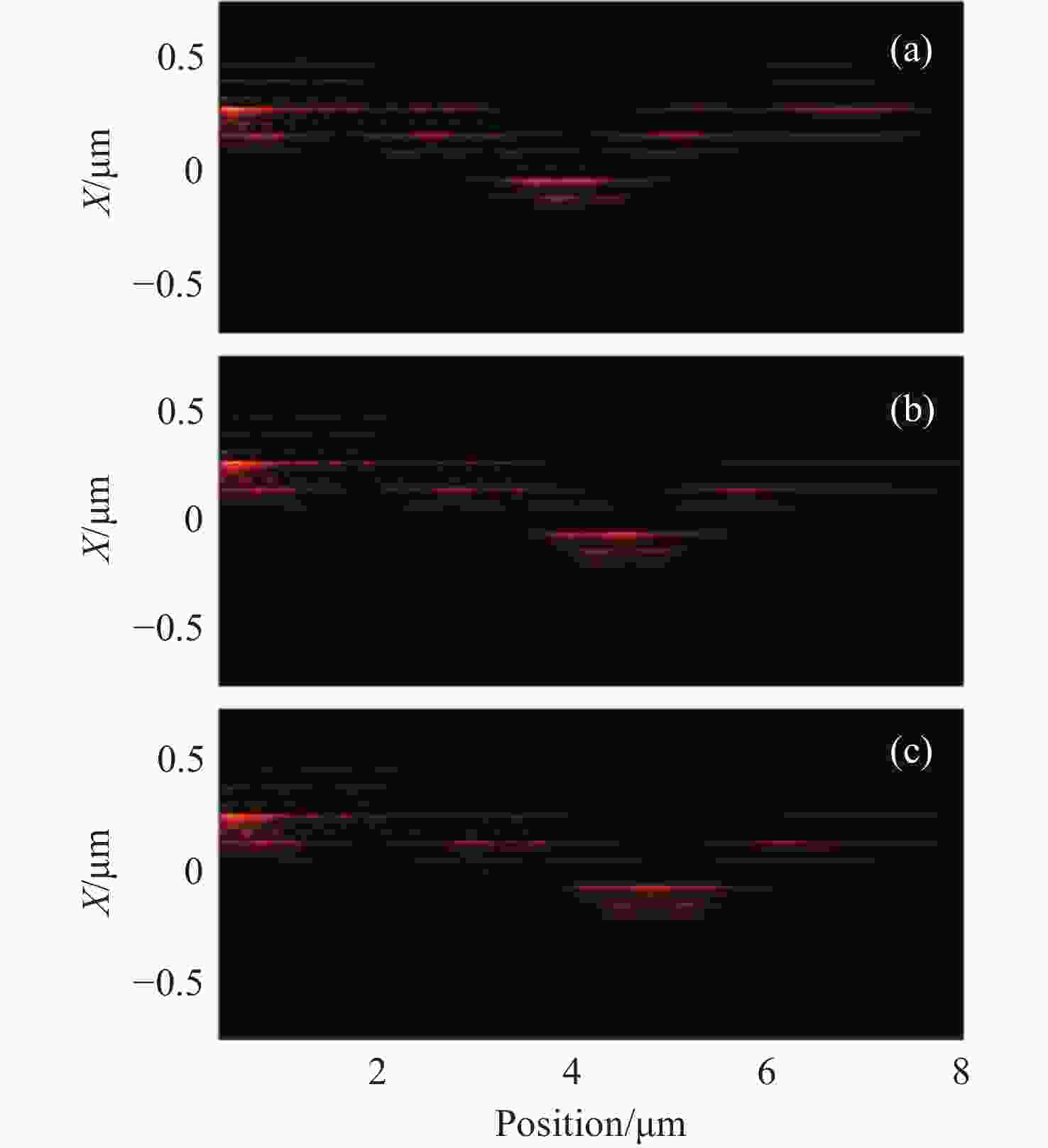
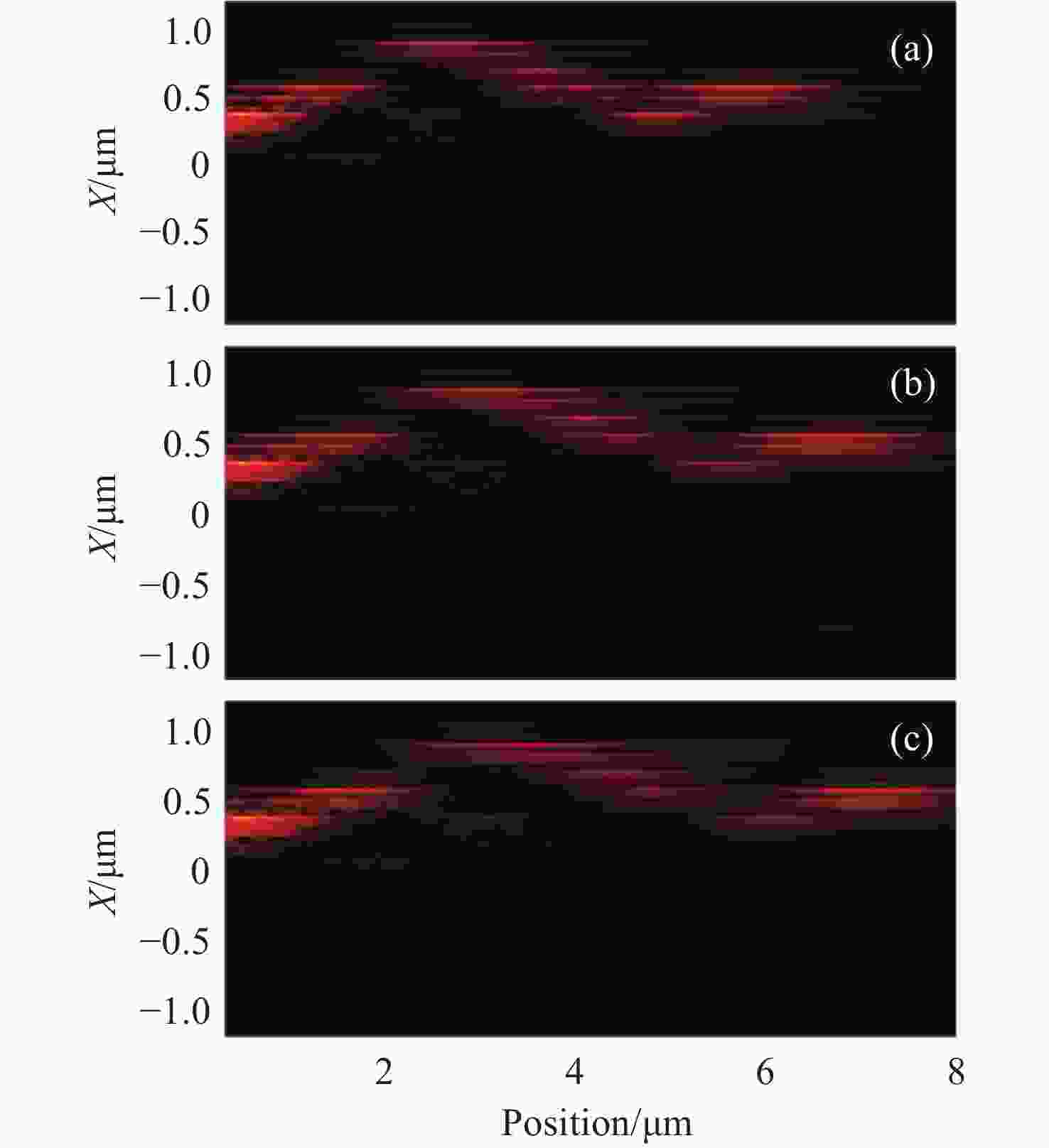
$ \left| {{H_y}} \right| $ simulated by the FDTD method for Gaussian pulses with$ \lambda = 460 $ nm and$ \lambda = $ $ 488 $ nm, respectively. (c) The simulated period of the BLO in the waveguide arrays depends on the incident light wavelength ($ \lambda = $ 405, 460, 488, 514, 532, 589, 635, 650, 694 nm, respectively).
Figure 3. Contours of magnetic field intensity
$ \left| {{H_y}} \right| $ for a Gaussian pulse impinging on the positions of$ x = 0.34 $ ,$ x = 0 $ and$ x = - 0.34 $ are shown in (a), (b), and (c) respectively.
Figure 4. (a)−(c) Contours of magnetic field intensity
$ \left| {{H_y}} \right| $ for Gaussian pulse impinging on the position of$ x = 0.21 $ . -
[1] BLOCH F. Über die quantenmechanik der elektronen in kristallgittern[J]. Zeitschrift für Physik, 1929, 52(7): 555-600. [2] FELDMANN J, LEO K, SHAH J, et al. Optical investigation of Bloch oscillations in a semiconductor superlattice[J]. Physical Review B, 1992, 46(11): 7252-7255. doi: 10.1103/PhysRevB.46.7252 [3] MORANDOTTI R, PESCHEL U, AITCHISON J S, et al. Experimental observation of linear and nonlinear optical bloch oscillations[J]. Physical Review Letters, 1999, 83(23): 4756-4759. doi: 10.1103/PhysRevLett.83.4756 [4] DENG M, COTRUFO M, WANG J, et al. Broadband angular spectrum differentiation using dielectric metasurfaces[J]. Nature Communications, 2024, 15(1): 2237. doi: 10.1038/s41467-024-46537-9 [5] HUANG ZH R, ZHENG Y Q, LI J H, et al. High-resolution metalens imaging polarimetry[J]. Nano Letters, 2023, 23(23): 10991-10997. doi: 10.1021/acs.nanolett.3c03258 [6] DENG M, COTRUFO M, WANG J, et al. Broadband angular spectrum differentiation using dielectric metasurfaces[J]. Nature Communications, 2024, 15(1): 2237. . [7] LENZ G, TALANINA I, DE STERKE C M. Bloch oscillations in an array of curved optical waveguides[J]. Physical Review Letters, 1999, 83(5): 963-966. doi: 10.1103/PhysRevLett.83.963 [8] BREID B M, WITTHAUT D, KORSCH H J. Bloch-Zener oscillations[J]. New Journal of Physics, 2006, 8: 110. doi: 10.1088/1367-2630/8/7/110 [9] BLOCK A, ETRICH C, LIMBOECK T, et al. Bloch oscillations in plasmonic waveguide arrays[J]. Nature Communications, 2014, 5(1): 3483. doi: 10.1038/ncomms4483 [10] WETTER H, FEDOROVA Z, LINDEN S. Observation of the Wannier–Stark ladder in plasmonic waveguide arrays[J]. Optics Letters, 2022, 47(12): 3091-3094. doi: 10.1364/OL.458954 [11] ZHAO Y, CHEN Y, HOU ZH SH, et al. Polarization-dependent Bloch oscillations in optical waveguides[J]. Optics Letters, 2022, 47(3): 617-620. doi: 10.1364/OL.448090 [12] LI J H, HU G W, SHI L N, et al. Full-color enhanced second harmonic generation using rainbow trapping in ultrathin hyperbolic metamaterials[J]. Nature Communications, 2021, 12(1): 6425. doi: 10.1038/s41467-021-26818-3 [13] KHAN N, WANG P, FU Q D, et al. Observation of period-doubling Bloch oscillations[J]. Physical Review Letters, 2024, 132(5): 053801. doi: 10.1103/PhysRevLett.132.053801 [14] ZHANG ZH, LI Y, CHEN CH H, et al. Polychromatic photonic Floquet-Bloch oscillations[J]. Optics Express, 2024, 32(6): 10703-10714. doi: 10.1364/OE.519007 [15] SANCHIS-ALEPUZ H, KOSEVICH Y A, SÁNCHEZ-DEHESA J. Acoustic analogue of electronic Bloch oscillations and resonant Zener tunneling in ultrasonic superlattices[J]. Physical Review Letters, 2007, 98(13): 134301. doi: 10.1103/PhysRevLett.98.134301 [16] NATALE G, BLAND T, GSCHWENDTNER S, et al. Bloch oscillations and matter-wave localization of a dipolar quantum gas in a one-dimensional lattice[J]. Communications Physics, 2022, 5(1): 227. doi: 10.1038/s42005-022-01009-8 [17] ZHANG W X, YUAN H, WANG H T, et al. Observation of Bloch oscillations dominated by effective anyonic particle statistics[J]. Nature Communications, 2022, 13(1): 2392. doi: 10.1038/s41467-022-29895-0 [18] PRADHAN S K, XIAO B, SKUZA J R, et al. Effects of dielectric thickness on optical behavior and tunability of one-dimensional Ag/SiO2 multilayered metamaterials[J]. Optics Express, 2014, 22(10): 12486-12498. doi: 10.1364/OE.22.012486 [19] MAIER S A, BRONGERSMA M L, KIK P G, et al. Plasmonics—a route to nanoscale optical devices[J]. Advanced Materials, 2001, 13(19): 1501-1505. doi: 10.1002/1521-4095(200110)13:19<1501::AID-ADMA1501>3.0.CO;2-Z [20] ZHANG J X, ZHANG L D, XU W. Surface plasmon polaritons: physics and applications[J]. Journal of Physics D: Applied Physics, 2012, 45(11): 113001. doi: 10.1088/0022-3727/45/11/113001 [21] OZBAY E. Plasmonics: merging photonics and electronics at nanoscale dimensions[J]. Science, 2006, 311(5758): 189-193. doi: 10.1126/science.1114849 [22] ZHOU Y, LIU Q, WANG CH K, et al. Trapping effect and trajectory control of surface plasmon polaritons in a metal-dielectric-metal waveguide[J]. Physical Review A, 2020, 102(6): 063516. doi: 10.1103/PhysRevA.102.063516 [23] LIN W H, CHEN Y F, WANG W J. Array periodical nanofocusing effect in nanoscale three-dimensional surface plasmon polariton waveguide arrays[J]. Journal of the Optical Society of America B, 2020, 37(3): 762-766. doi: 10.1364/JOSAB.384450 [24] LIN W H, WANG W J. The spatial plasmonic Bloch oscillations in nanoscale three-dimensional surface plasmon polaritons metal waveguide arrays[J]. Optics Express, 2019, 27(17): 24591-24600. doi: 10.1364/OE.27.024591 [25] DAVOYAN A R, SHADRIVOV I V, SUKHORUKOV A A, et al. Plasmonic Bloch oscillations in chirped metal-dielectric structures[J]. Applied Physics Letters, 2009, 94(16): 161105. doi: 10.1063/1.3119666 [26] MEDINA-MAGALLÓN J E, PÉREZ-AGUILAR H, ZHEVANDROV-BOLSHAKOVA P, et al. Excitation of surface plasmon polaritons in photonic crystal waveguides that involve dispersive metamaterial[J]. Journal of Physics: Conference Series, 2019, 1221: 012010. doi: 10.1088/1742-6596/1221/1/012010 [27] LI ZH H, PANG X N, DONG J W, et al. Electromagnetic Bloch-like oscillations in one-dimensional quasicrystal consisting of negative permeability metamaterial[J]. Europhysics Letters, 2011, 95(3): 36004. doi: 10.1209/0295-5075/95/36004 [28] VASCONCELOS M S, ALBUQUERQUE E L. Plasmon-polariton fractal spectra in quasiperiodic multilayers[J]. Physical Review B, 1998, 57(5): 2826-2833. doi: 10.1103/PhysRevB.57.2826 [29] RAETHER H. Surface plasmons on smooth surfaces[M]//RAETHER H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings. Berlin, Heidelberg: Springer, 1988: 4-39. [30] LOURENÇO P, FANTONI A, FERNANDES M, et al. FDTD analysis of Aluminum/a-Si: H surface plasmon waveguides[J]. Proceedings of SPIE, 2018, 10526: 105262D. [31] VERSLEGERS L, CATRYSSE P B, YU Z F, et al. Deep-subwavelength focusing and steering of light in an aperiodic metallic waveguide array[J]. Physical Review Letters, 2009, 103(3): 033902. doi: 10.1103/PhysRevLett.103.033902 [32] MALPUECH G, KAVOKIN A, PANZARINI G, et al. Theory of photon Bloch oscillations in photonic crystals[J]. Physical Review B, 2001, 63(3): 035108. doi: 10.1103/PhysRevB.63.035108 -
下载:
计量
- 文章访问数: 55
- HTML全文浏览量: 24
- PDF下载量: 1
- 被引次数: 0
