Influencing factor analysis of the Principal Component Analysis for the characterization and restoration of phase aberrations resulting from atmospheric turbulence
doi: 10.37188/CO.EN-2024-0035
-
摘要:
为了有效表征、还原大气湍流造成的相位畸变，解决传统Zernike多项式方法引起的相位还原高频信息不足问题，提出了基于主成分分析法的畸变相位特征表征、还原方法，对可能影响主成分精度从而影响还原效果的因素进行研究。首先建立了几组包含满足Von-Karman功率谱的畸变相位的原始数据集，几组数据集样本数量不等，并生成了
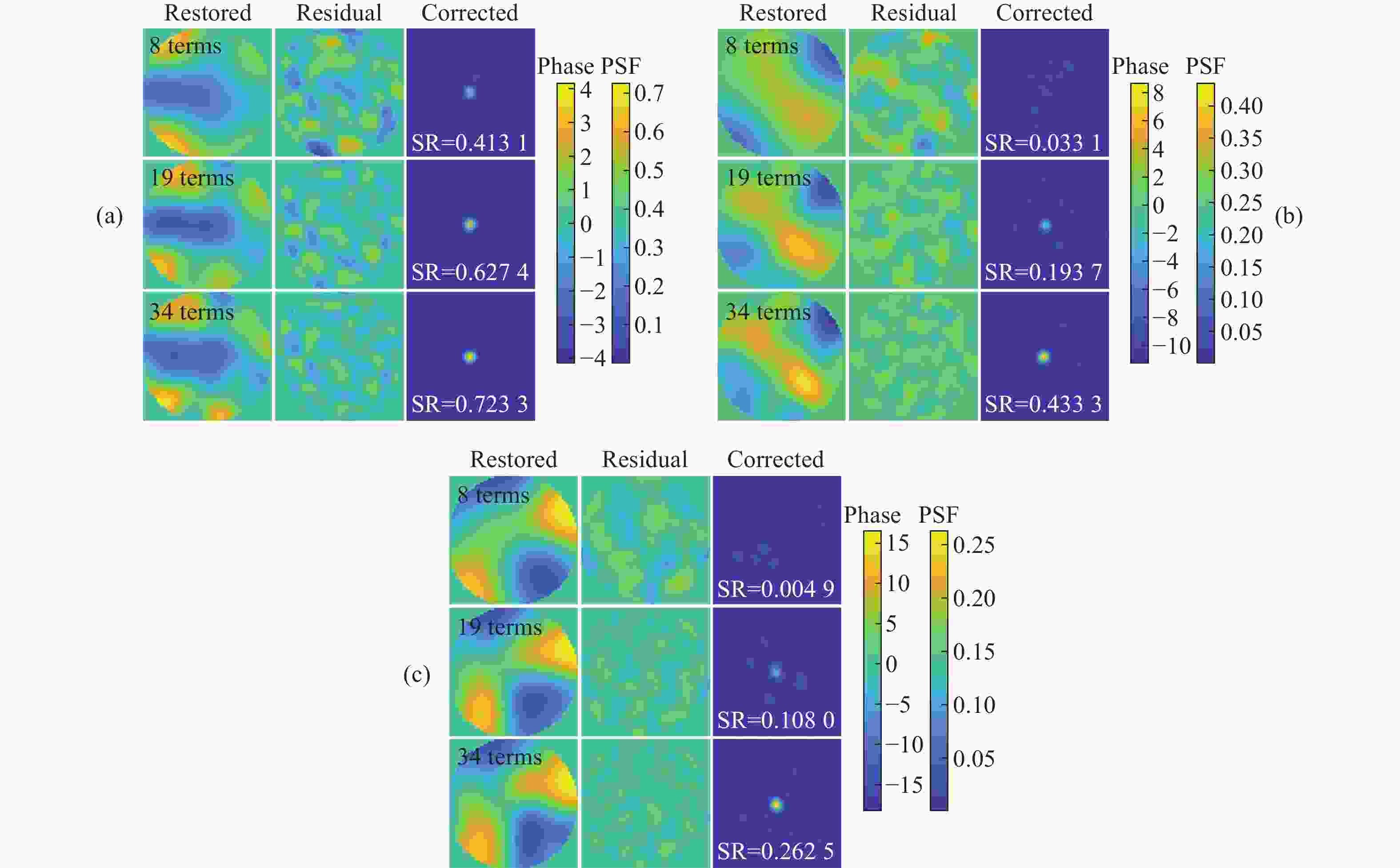
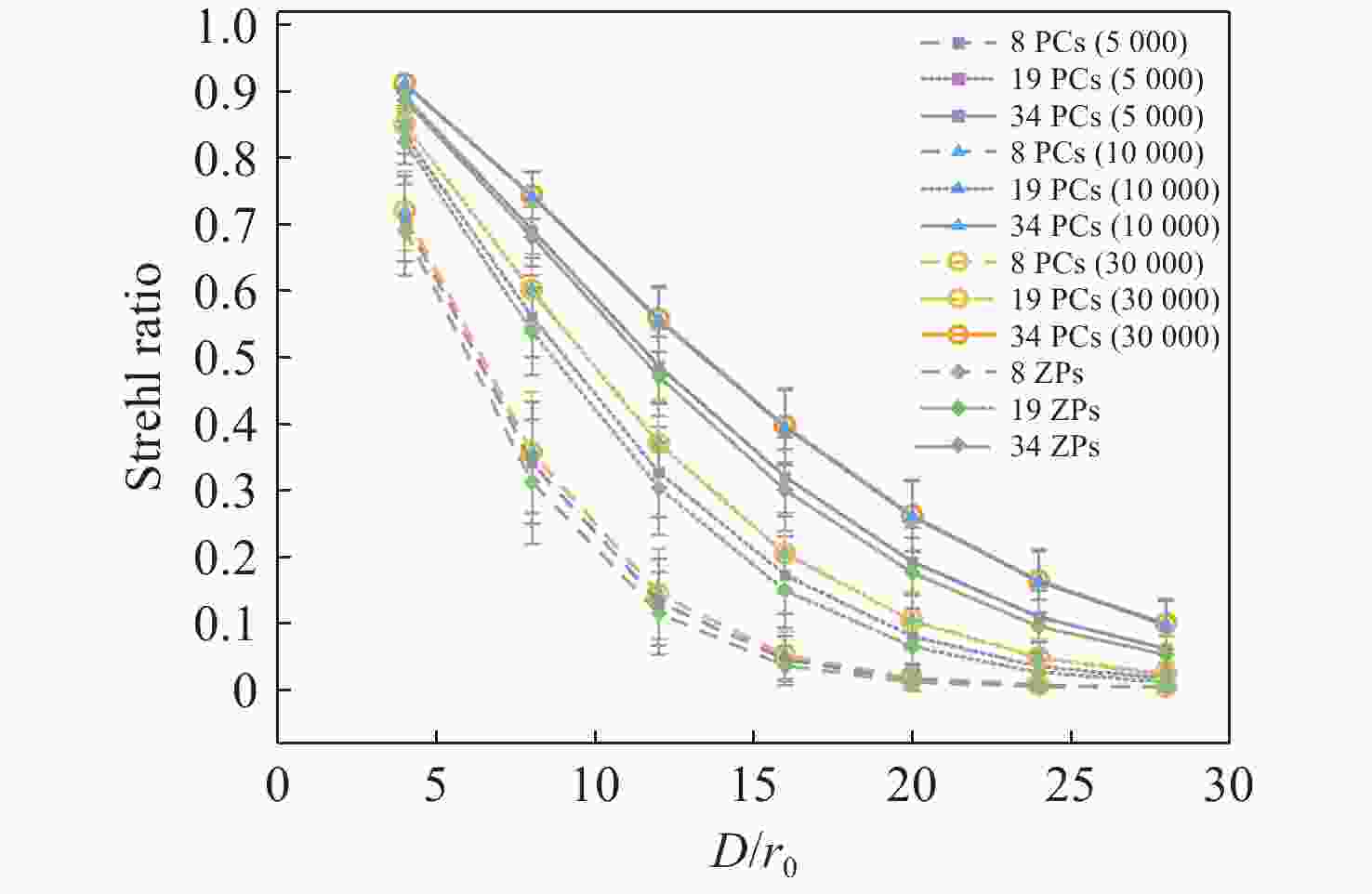
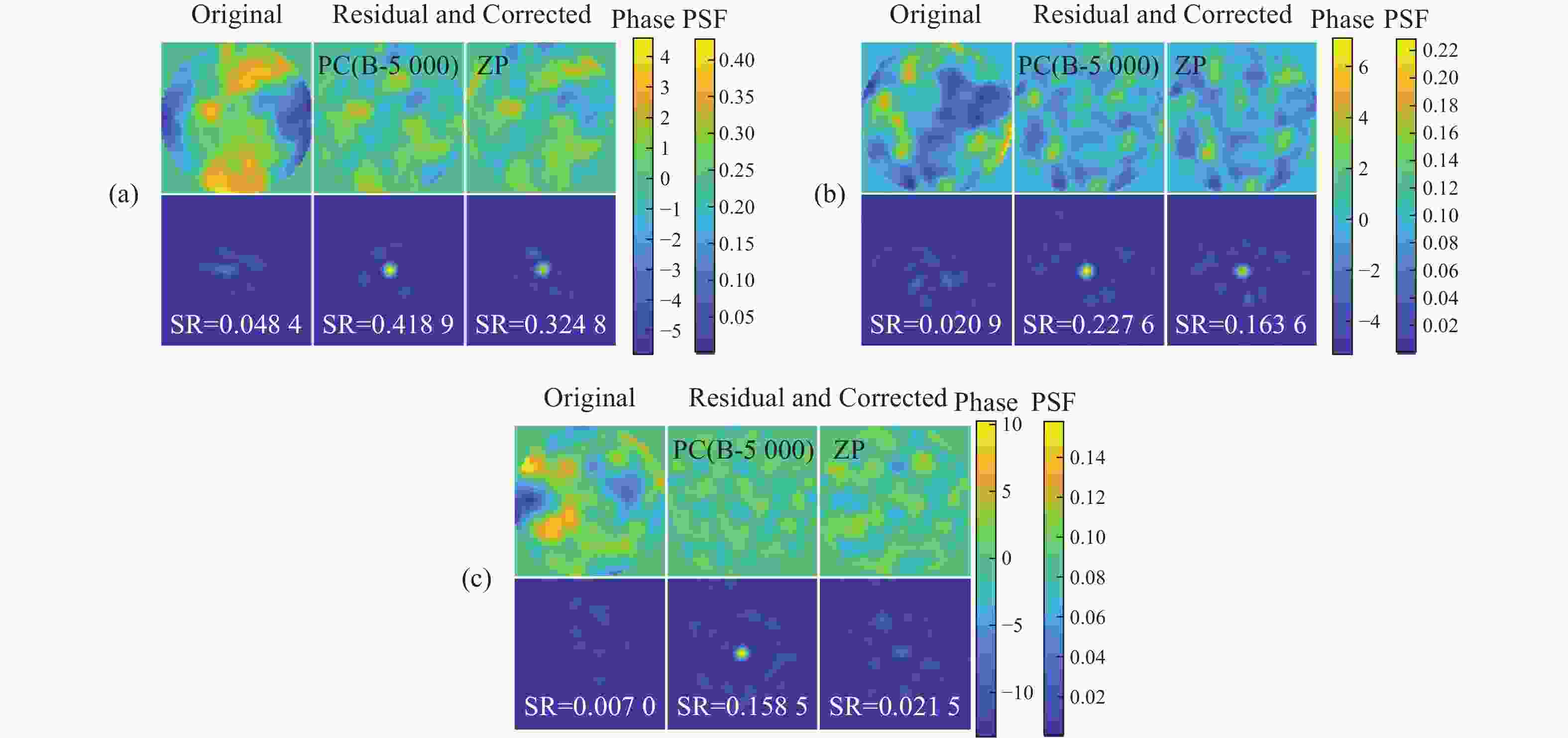
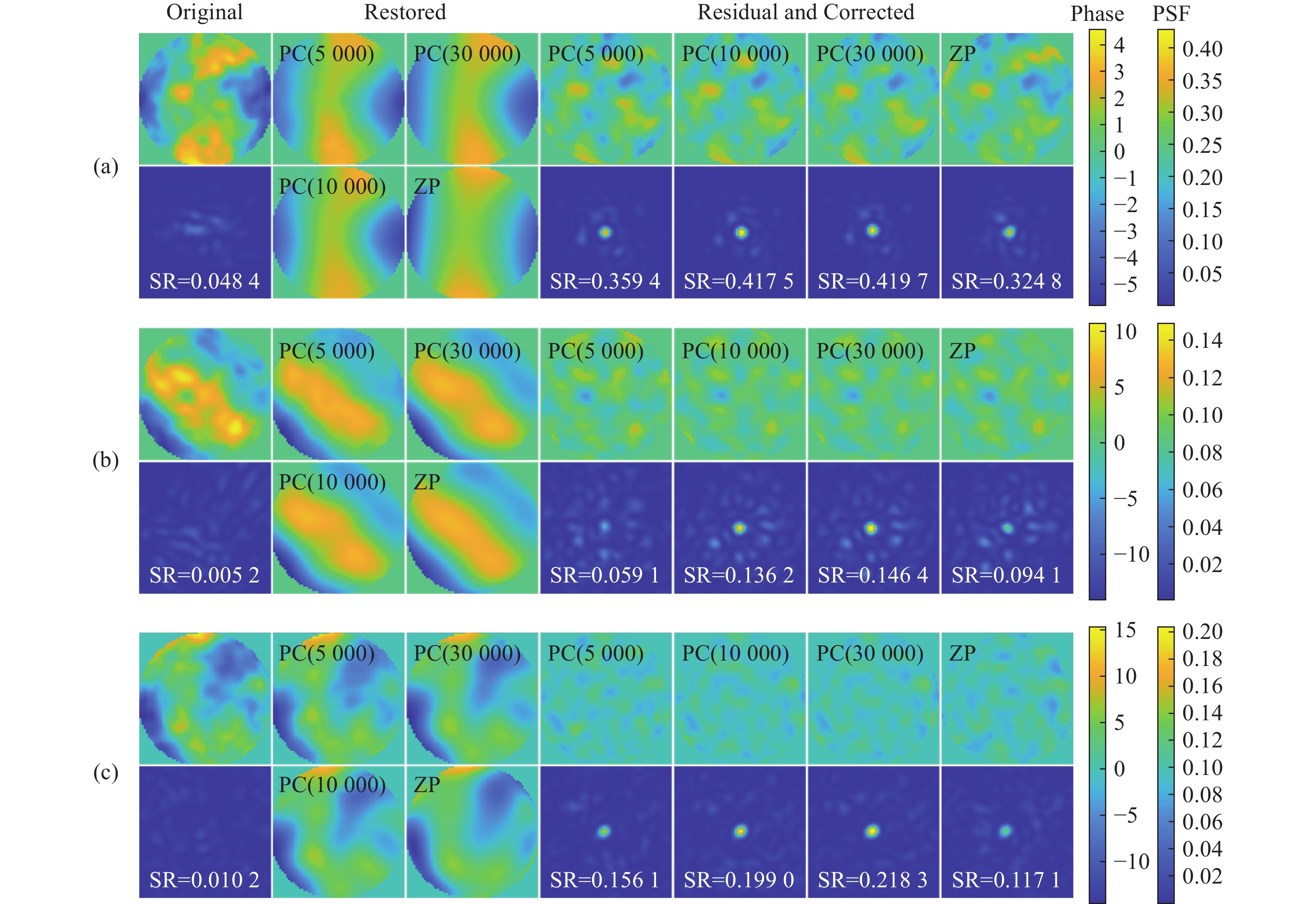
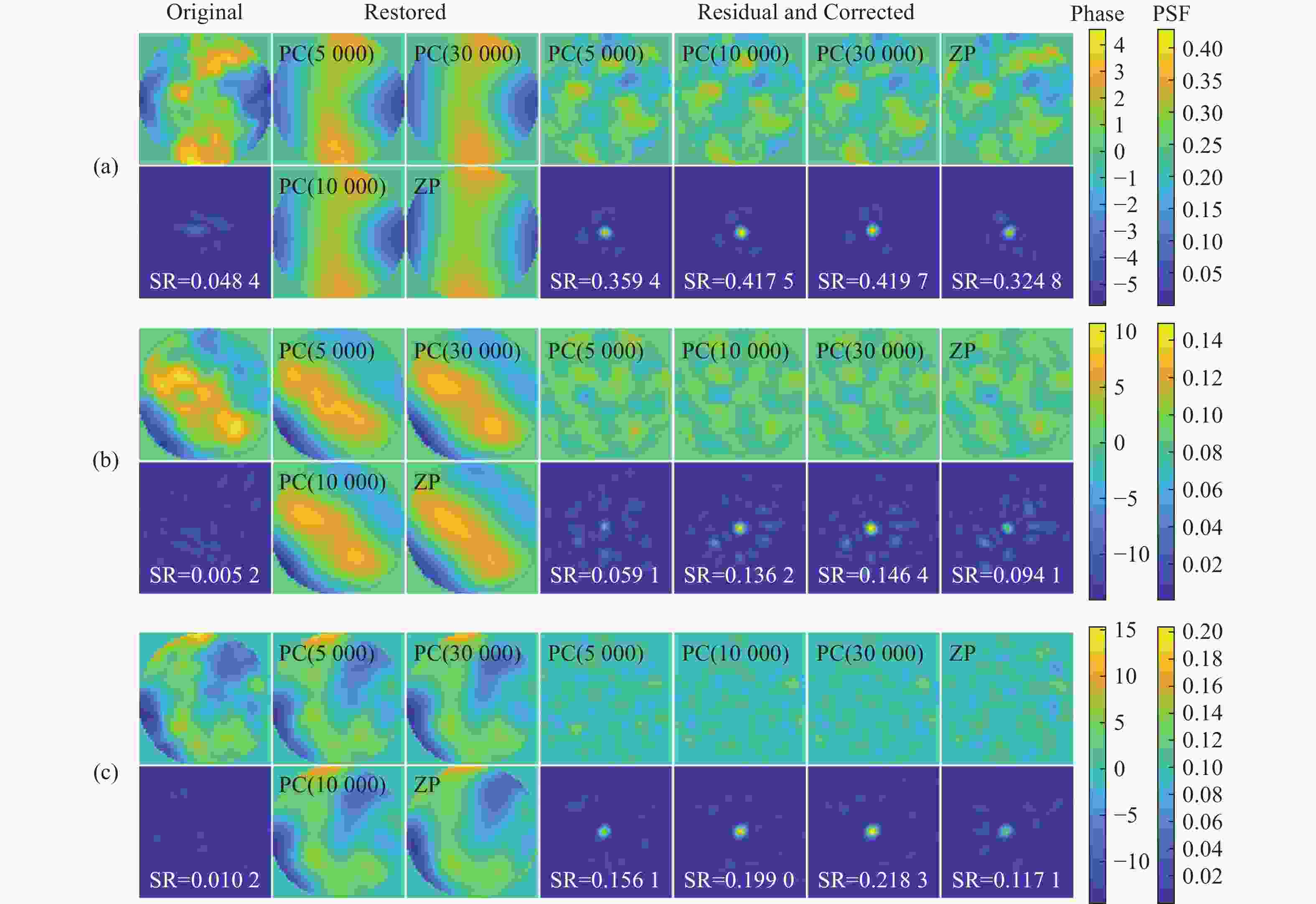
D/r 0 采样间隔分别为1和10的样本空间，D/r 0 用于描述湍流强度，其中r 0 是大气相干长度，D 是光瞳直径。接着建立了不同湍流强度下畸变相位的测试集数据。之后从不同原始数据集中提取对应的主成分，并分别使用相同项数的主成分与Zernike多项式对同一组测试集畸变相位进行还原。最终对比还原结果，分析原始数据样本量和D/r 0 采样间隔对主成分精度的影响。实验结果表明结果：更大的D/r 0 采样间隔可以在原始数据量有限的情况下保证主成分的泛化能力和鲁棒性，从而帮助实际应用中快速实现模型的高精度部署；在测试集D/r 0 =24的相对湍流较强的环境下，使用34阶主成分可以将校正后光斑Strehl比从原始的0.007提升至0.1585 ，而同样使用34阶Zernike还原后的光斑Strehl比仅为0.0215 ，几乎没有校正效果。可以看出基于主成分分析法的大气湍流相位畸变表征和还原方法优于Zernike多项式，可以为基于模型和深度学习的自适应光学校正提供参考。-
关键词:
- 相位畸变 /
- 大气湍流 /
- 主成分分析法 /
- Zernike多项式
Abstract:Restoration of phase aberrations is crucial for addressing atmospheric turbulence in light propagation. Traditional restoration algorithms based on Zernike polynomials (ZPs) often encounter challenges related to high computational complexity and insufficient capture of high-frequency phase aberration components, so we proposed a Principal-Component-Analysis-based method for representing phase aberrations. This paper discusses factors influencing the accuracy of restoration using Principal Components (PCs), mainly sample space size and the sampling interval of
D/r 0 , which is used to characterize the strength, withr 0 being the atmospheric coherence length andD being the pupil diameter, on the basis of characterizing phase aberrations by PCs. The experimental results show that a largerD/r 0 sampling interval can ensure the generalization ability and robustness of the principal components in the case of a limited amount of original data, which can help to achieve high-precision deployment of the model in practical applications quickly. In the environment with relatively strong turbulence in the test set ofD/r 0 = 24, the use of 34 terms of PCs can improve the corrected Strehl ratio (SR) from 0.007 to0.1585 , while the Strehl ratio of the light spot after restoration using 34 terms of ZPs is only0.0215 , demonstrating almost no correction effect. The results indicate that PCs can serve as a better alternative in representing and restoring the characteristics of atmospheric turbulence induced phase aberrations. These findings pave the way to use PCs of phase aberrations with fewer terms than traditional ZPs to achieve data dimensionality reduction, and offer a reference to accelerate and stabilize the model and deep learning based adaptive optics correction. -
图 1 不同数据量提取的PCs与ZPs还原相位畸变的效果示例(a)
$ D/{r}_{0}=8， $ 使用8项模式；(b)$ D/{r}_{0}=16， $ 使用19项模式；(c)$ D/{r}_{0}=24， $ 使用34项模式Figure 1. Examples of restoration by ZPs vs PCs obtained from different sample space sizes (a)
$D/{r_0} = 8 ,$ using the first 8 terms; (b)$D/{r_0} = 16 ,$ using the first 19 terms; (c)$D/{r_0} = 24 ,$ using the first 34 terms.
图 2 相同湍流强度下使用不同数量PCs模式的还原效果示例
Figure 2. Examples of restoration by 8, 19, and 34 PCs (a)
$D/{r_0} = 8$ ; (b)$D/{r_0} = 16$ ; (c)$D/{r_0} = 24$ 
图 3 使用不同数据量提取的PCs与ZPs还原相位畸变后均值SR对比
Figure 3. Comparison of mean Strehl ratio after phase aberration restoration by ZPs and PCs obtained from different sample space sizes
图 4 使用A-
5000 与B-5000提取的PCs还原相位畸变后均值SR对比Figure 4. Comparison of the mean Strehl ratio after phase aberration restoration by PCs obtained from A-5000 and B-5000
图 5 使用相等数量的PCs（从B-5000提取）和ZPs模式还原相位畸变效果示例(a)
$ D/{r}_{0}=8， $ 使用8项模式；(b)$ D/{r}_{0}= $ $ 16， $ 使用19项模式；(c)$ D/{r}_{0}=24， $ 使用34项模式Figure 5. Examples of restoration of phase aberrations by the equivalent terms of ZPs vs PCs obtained from B-5000 (a)
$D/{r_0} = 8 ,$ using the first 8 terms; (b)$D/{r_0} = 16 ,$ using the first 19 terms; (c)$D/{r_0} = 24 ,$ using the first 34 terms.表 1 Comparison of the mean Strehl ratio after phase restoration by PCs obtained from B-5000 and A-30000 (The first row 4-28 indicates the
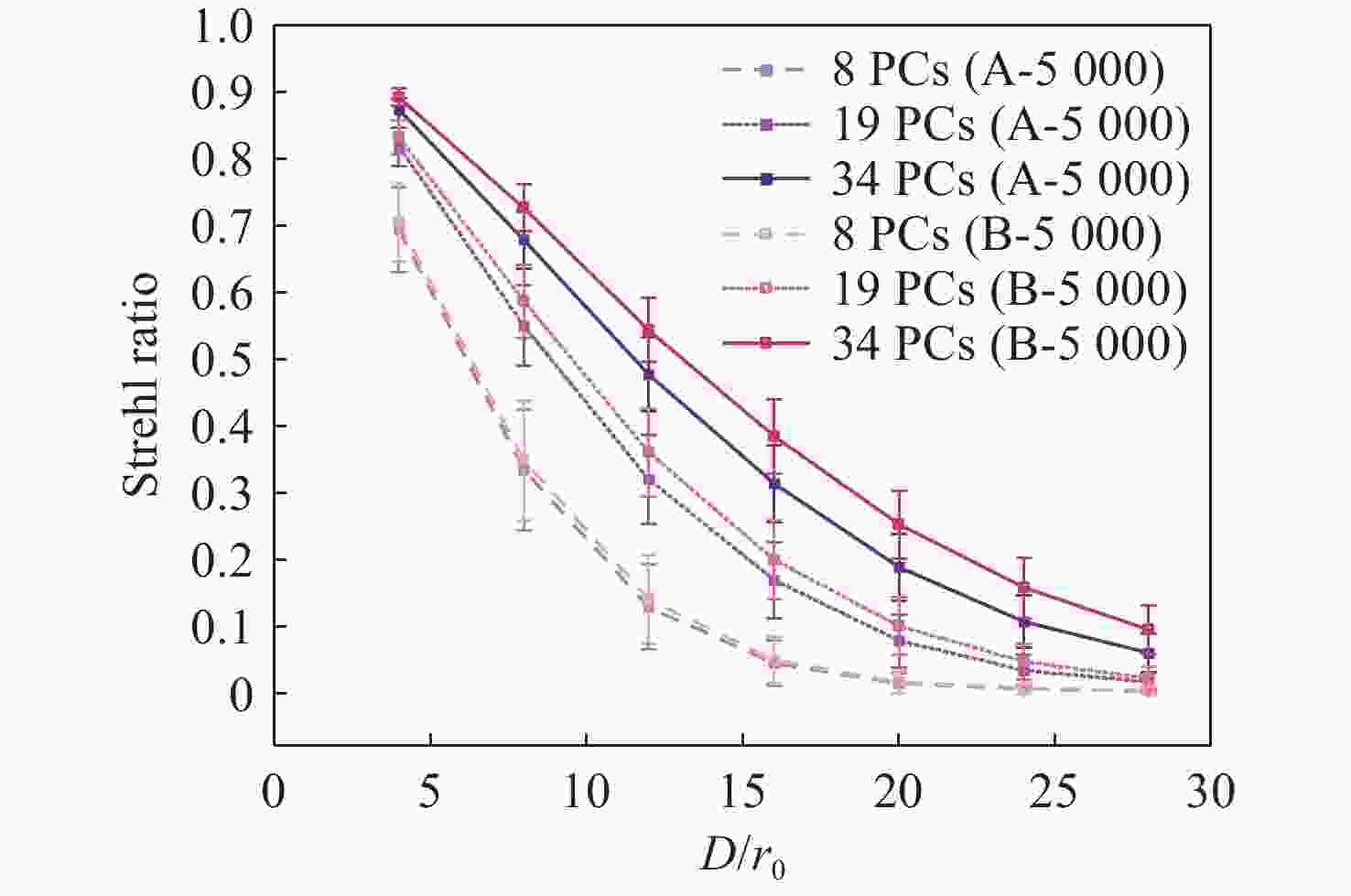
$D/{r_0}$ of test sets)Table 1. Comparison of the mean Strehl ratio after phase restoration by PCs obtained from B-5000 and A-30000 (The first row 4-28 indicates the
$D/{r_0}$ of test sets)Terms D/r0 N 4 8 12 16 20 24 28 8 5000 0.719 0.3563 0.1437 0.0515 0.0177 0.0072 0.0046 30000 0.7204 0.3577 0.1439 0.0521 0.0176 0.0073 0.0047 19 5000 0.8496 0.5989 0.368 0.204 0.103 0.0482 0.0235 30000 0.8505 0.6011 0.3702 0.2049 0.1041 0.0488 0.024 34 5000 0.9101 0.7412 0.5547 0.3925 0.2582 0.1616 0.0978 30000 0.9108 0.7436 0.5582 0.3978 0.2636 0.1644 0.1002 
下载: 导出CSV
-
[1] MAHAJAN V N. Aberrations of diffracted wave fields. I. Optical imaging[J]. Journal of the Optical Society of America A, 2000, 17(12): 2216-2222. doi: 10.1364/JOSAA.17.002216 [2] ANGEL J R P, WIZINOWICH P, LLOYD-HART M, et al. Adaptive optics for array telescopes using neural-network techniques[J]. Nature, 1990, 348(6298): 221-224. doi: 10.1038/348221a0 [3] SANDLER D G, BARRETT T K, PALMER D A, et al. Use of a neural network to control an adaptive optics system for an astronomical telescope[J]. Nature, 1991, 351(6324): 300-302. doi: 10.1038/351300a0 [4] JIA P, MA M Y, CAI D M, et al. Compressive Shack–Hartmann wavefront sensor based on deep neural networks[J]. Monthly Notices of the Royal Astronomical Society, 2021, 503(3): 3194-3203. doi: 10.1093/mnras/staa4045 [5] HARTLIEB S, WANG ZH, RÜDINGER A, et al. Large dynamic range Shack–Hartmann wavefront sensor based on holographic multipoint generation and pattern correlation[J]. Optical Engineering, 2024, 63(2): 024107. [6] VOLKOV M V, BOGACHEV V A, STARIKOV F A, et al. Numerical study of dynamic adaptive phase correction of radiation turbulent distortions and estimation of their frequency bandwidth with a Shack–Hartmann wavefront sensor[J]. Atmospheric and Oceanic Optics, 2022, 35(3): 250-257. doi: 10.1134/S1024856022030174 [7] LI P, TANG F, WANG X ZH. Relationship between shear ratio and reconstruction accuracy in lateral shearing interferometry[J]. Optical Engineering, 2020, 59(3): 034113. [8] SONG J W, MIN J W, YUAN X, et al. Quadriwave lateral shearing interferometry quantitative phase imaging based on 2D Ronchi phase grating[J]. Acta Photonica Sinica, 2022, 51(11): 1118001. (in Chinese). doi: 10.3788/gzxb20225111.1118001 [9] SINHA A, LEE J, LI SH, et al. Lensless computational imaging through deep learning[J]. Optica, 2017, 4(9): 1117-1125. doi: 10.1364/OPTICA.4.001117 [10] CHEN M A, JIN X Q, LI SH B, et al. Compensation of turbulence-induced wavefront aberration with convolutional neural networks for FSO systems[J]. Chinese Optics Letters, 2021, 19(11): 110601. doi: 10.3788/COL202119.110601 [11] LOHANI S, GLASSER R T. Turbulence correction with artificial neural networks[J]. Optics Letters, 2018, 43(11): 2611-2614. doi: 10.1364/OL.43.002611 [12] GUO Y M, ZHONG L B, MIN L, et al. Adaptive optics based on machine learning: a review[J]. Opto-Electronic Advances, 2022, 5(7): 200082. doi: 10.29026/oea.2022.200082 [13] PAINE S W, FIENUP J R. Machine learning for improved image-based wavefront sensing[J]. Optics Letters, 2018, 43(6): 1235-1238. doi: 10.1364/OL.43.001235 [14] NISHIZAKI Y, VALDIVIA M, HORISAKI R, et al. Deep learning wavefront sensing[J]. Optics Express, 2019, 27(1): 240-251. doi: 10.1364/OE.27.000240 [15] GE X L, ZHU L CH, GAO Z Y, et al. Experimental demonstration of wavefront reconstruction and correction techniques for variable targets based on distorted grating and deep learning[J]. Optics Express, 2024, 32(10): 17775-17792. doi: 10.1364/OE.519163 [16] WANG Q T, TONG SH F, XU Y H. On simulation and verification of the atmospheric turbulent phase screen with Zernike polynomials[J]. Infrared and Laser Engineering, 2013, 42(7): 1907-1911. (in Chinese). doi: 10.3969/j.issn.1007-2276.2013.07.046 [17] SIDDIK A B, SANDOVAL S, VOELZ D, et al. Deep learning estimation of modified Zernike coefficients and recovery of point spread functions in turbulence[J]. Optics Express, 2023, 31(14): 22903-22913. doi: 10.1364/OE.493229 [18] LV H L, FU SH J, ZHANG C M, et al. Speckle noise reduction of multi-frame optical coherence tomography data using multi-linear principal component analysis[J]. Optics Express, 2018, 26(9): 11804-11818. doi: 10.1364/OE.26.011804 [19] ZHANG Q, XIAO G, LAN Y Q, et al. Atmospheric turbulence detection by PCA approach[J]. Aerospace Systems, 2019, 2(1): 15-20. doi: 10.1007/s42401-018-0012-1 [20] TERRERI A, PEDICHINI F, DEL MORO D, et al. Neural networks and PCA coefficients to identify and correct aberrations in adaptive optics[J]. Astronomy & Astrophysics, 2022, 666: A70. [21] SCHMIDT J D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB[M]. Bellingham: SPIE, 2010. [22] NOLL R J. Zernike polynomials and atmospheric turbulence[J]. Journal of the Optical Society of America, 1976, 66(3): 207-211. doi: 10.1364/JOSA.66.000207 [23] LANE R G, GLINDEMANN A, DAINTY J C. Simulation of a Kolmogorov phase screen[J]. Waves in Random Media, 1992, 2(3): 209-224. doi: 10.1088/0959-7174/2/3/003 -
下载:
计量
- 文章访问数: 96
- HTML全文浏览量: 30
- PDF下载量: 5
- 被引次数: 0
