Figure 1.  Schematic diagram of an open quantum battery composed of a moving atom in a lossy cavity. The quantum battery moves at a constant velocity along the z-axis in the cavity.

Figure 2.  The dynamics of the ergotropy at different velocities in a non-Markovian environment for $ {W_0} = 1 \times $${{10}^9}{\gamma _0}, \lambda / {{\gamma _0}} = 0.01, \theta = {\text{π}} $.

Figure 3.  The dynamics of the ergotropy at different velocities in a Markovian environment for $ {W_0} = 1 \times {{10}^9}{\gamma _0}, $$ \lambda / {{\gamma _0}}= 5, \theta = {\text{π}} $.

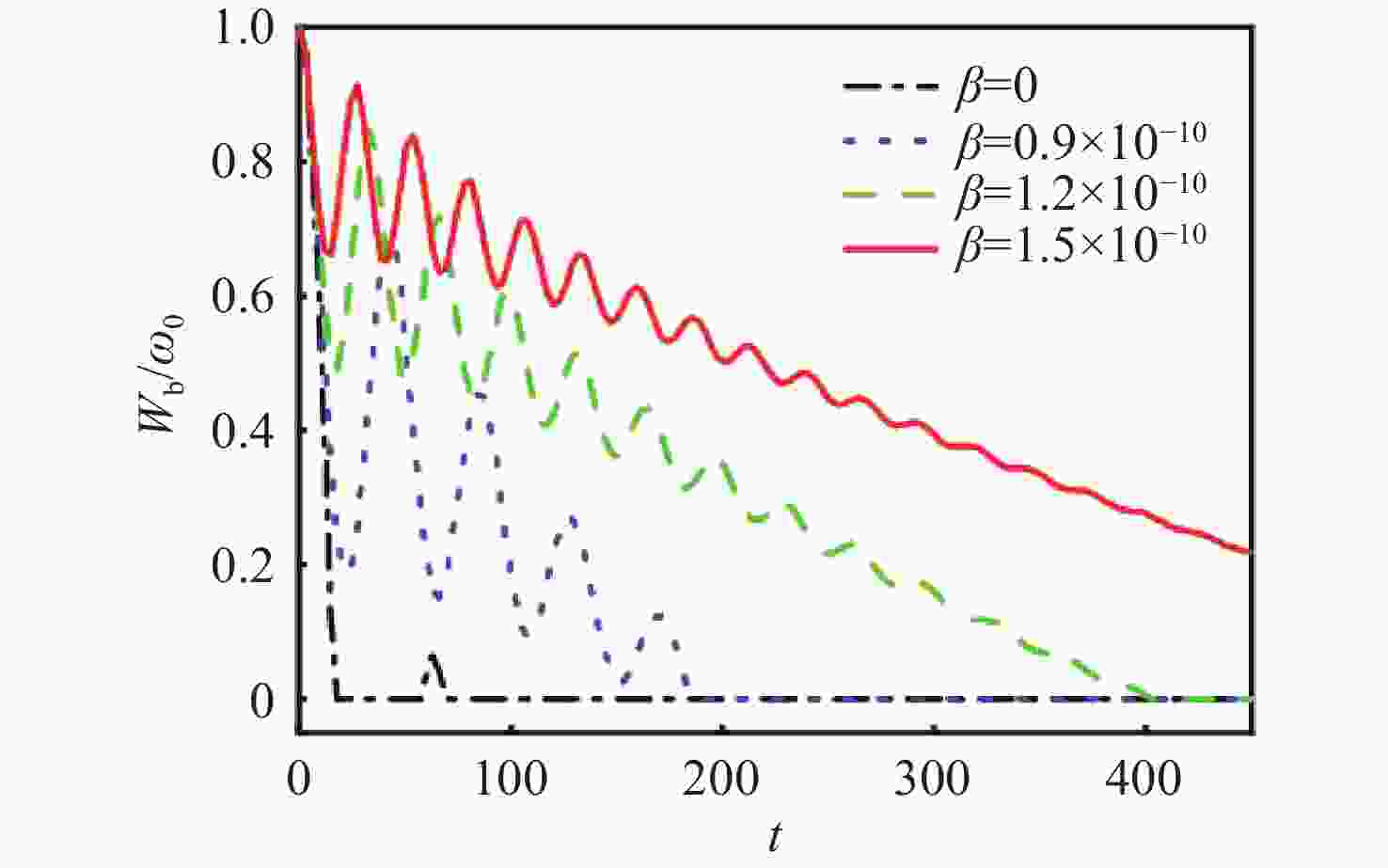
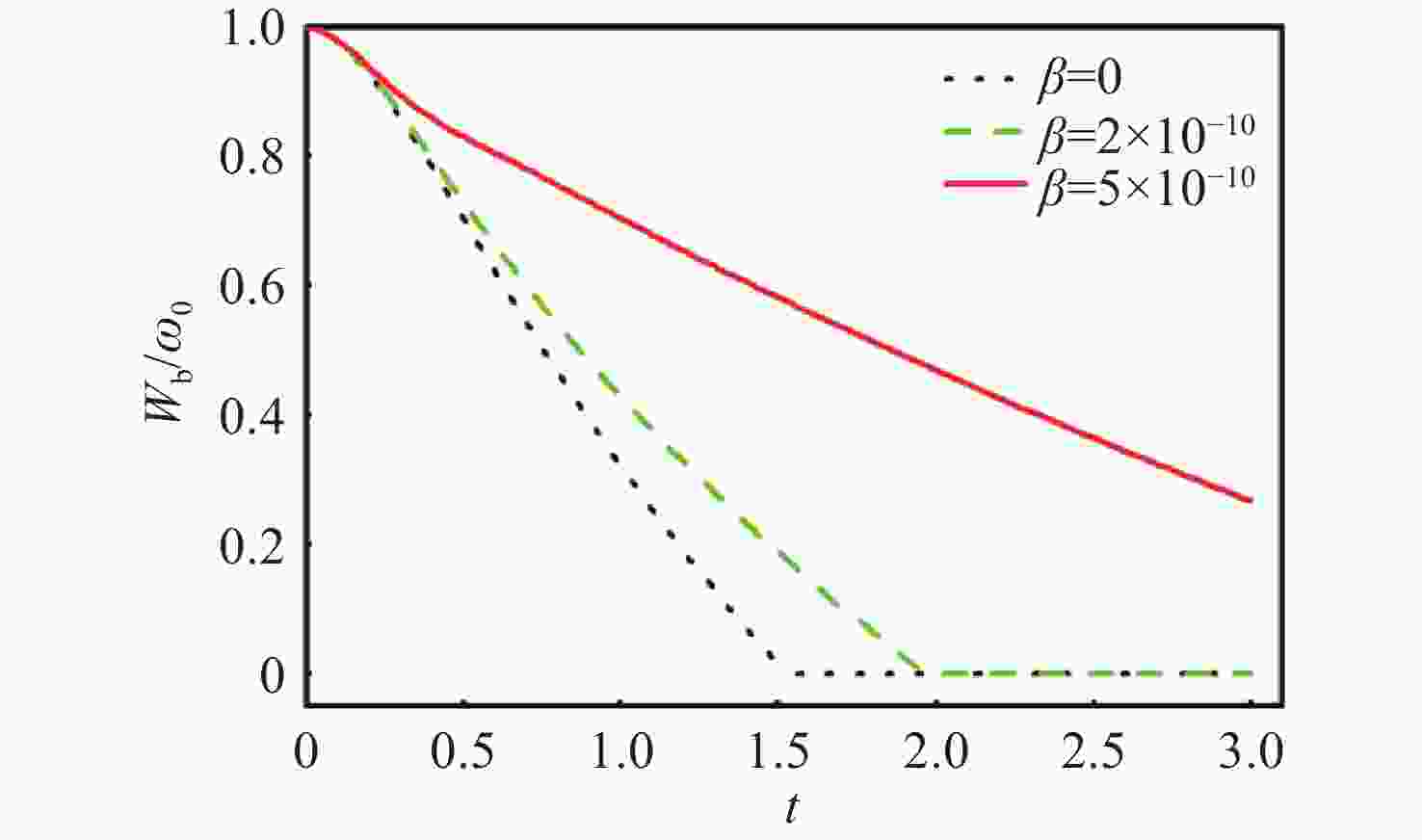
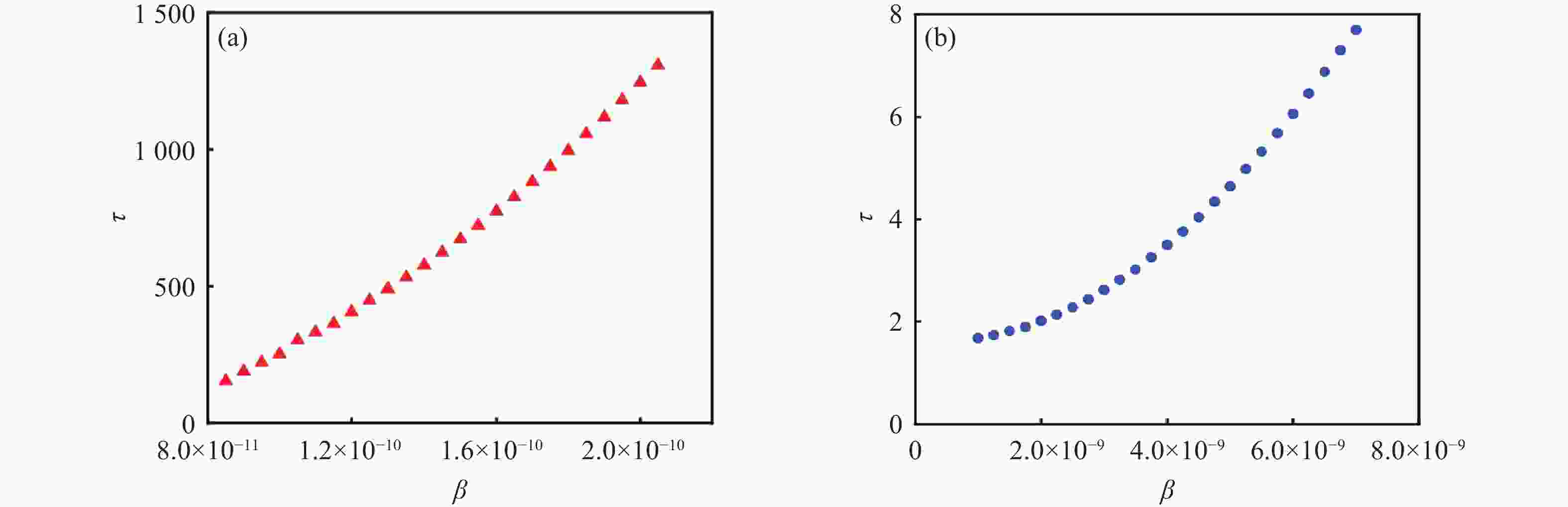
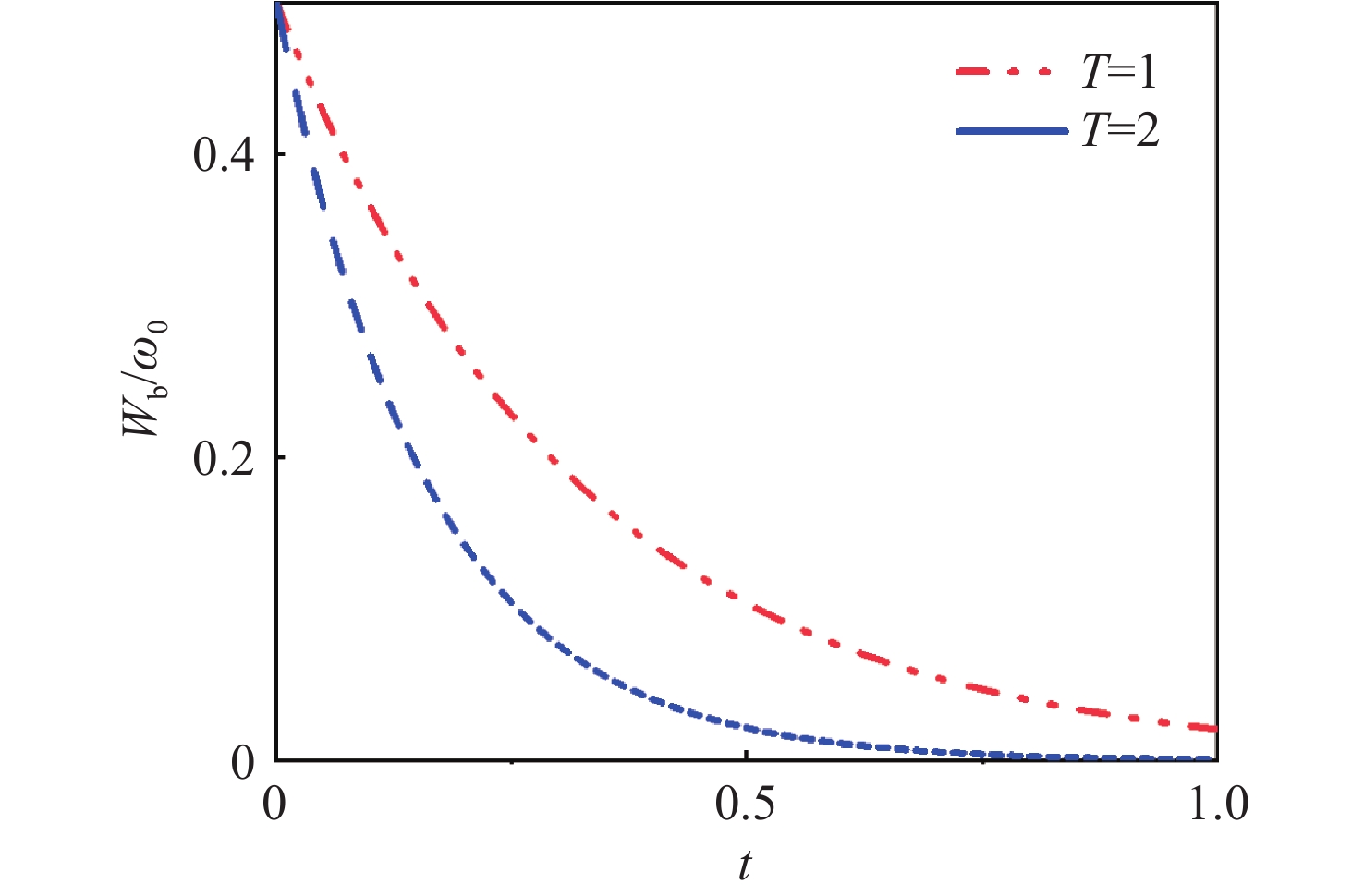
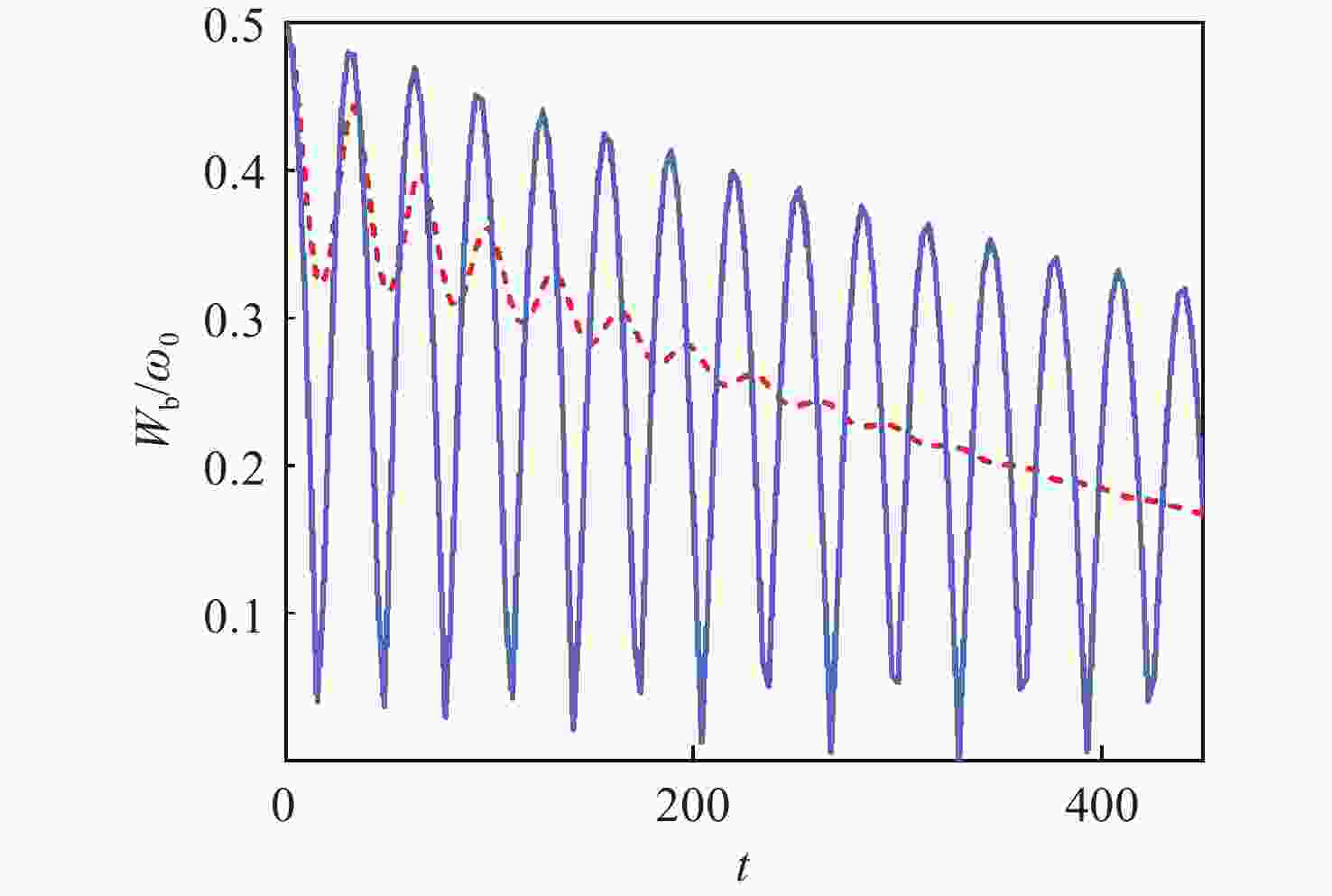
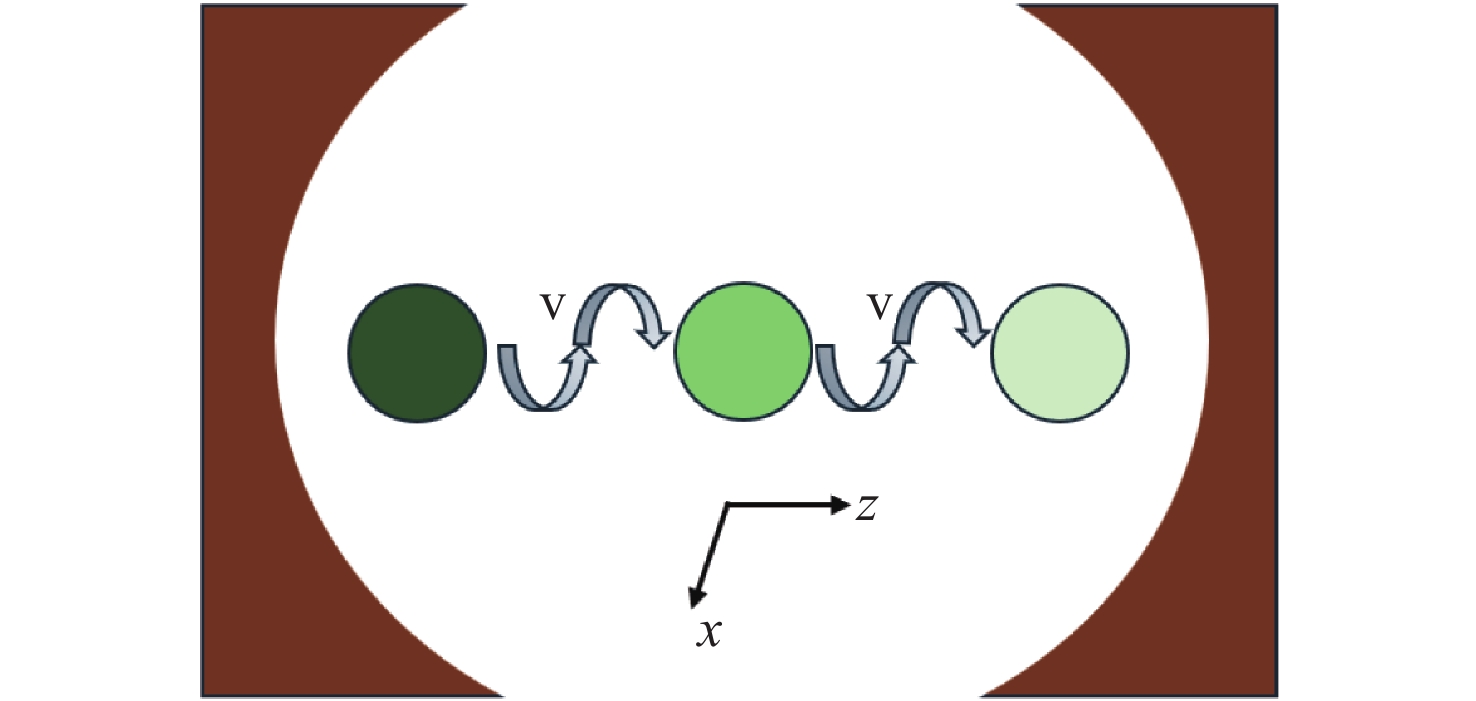
Figure 4.  The discharge lifetime as a function of atom velocity in bth Markovian and non-Markovian environments for $ {W_0} = 1 \times {10^9}{\gamma _0}, \theta = {\text{π}} . $ (a) Non-Markovian dynamics with ${\lambda \mathord{\left/ {\vphantom {\lambda {{\gamma _0}}}} \right. } {{\gamma _0}}} = 0.01. $ (b) Markovian dynamics with $ {\lambda \mathord{\left/ {\vphantom {\lambda {{\gamma _0}}}} \right. } {{\gamma _0}}} = 5. $

Figure 5.  The contour of the discharge efficiency of a quantum battery as a function of the coupling strength and the velocity. We set the parameters as $ {W_0} = 1 \times {10^9}{\gamma _0}, \theta = {\text{π}} /2$.

Figure 6.  The plot of the ergotropy variation induced by temperature changes inherent in the SGAD channel. The parameter settings are $ s = 0.5 $ and $ {\phi _s} = 0. $

Figure 7.  The influence of RTN channel and atomic motion on the ergotropy in quantum batteries. The red line represents the moving atoms in Fig. 1, while the blue line indicates the effect of the RTN channels. The parameter settings are $ \beta = 1.2 \times {10^{ - 10}}, \theta = {\text{π}} /2, $$ a = 0.05,\Gamma = 0.001$.

Figure 8.  The ergotropy evolves in a quantum battery of two simultaneously moving atoms. Atoms at the same velocity, the red solid line represents the maximum coherence state $ |{\psi _b}(0)\rangle = \dfrac{1}{{\sqrt 2 }}(|eg\rangle + |ge\rangle ) $.