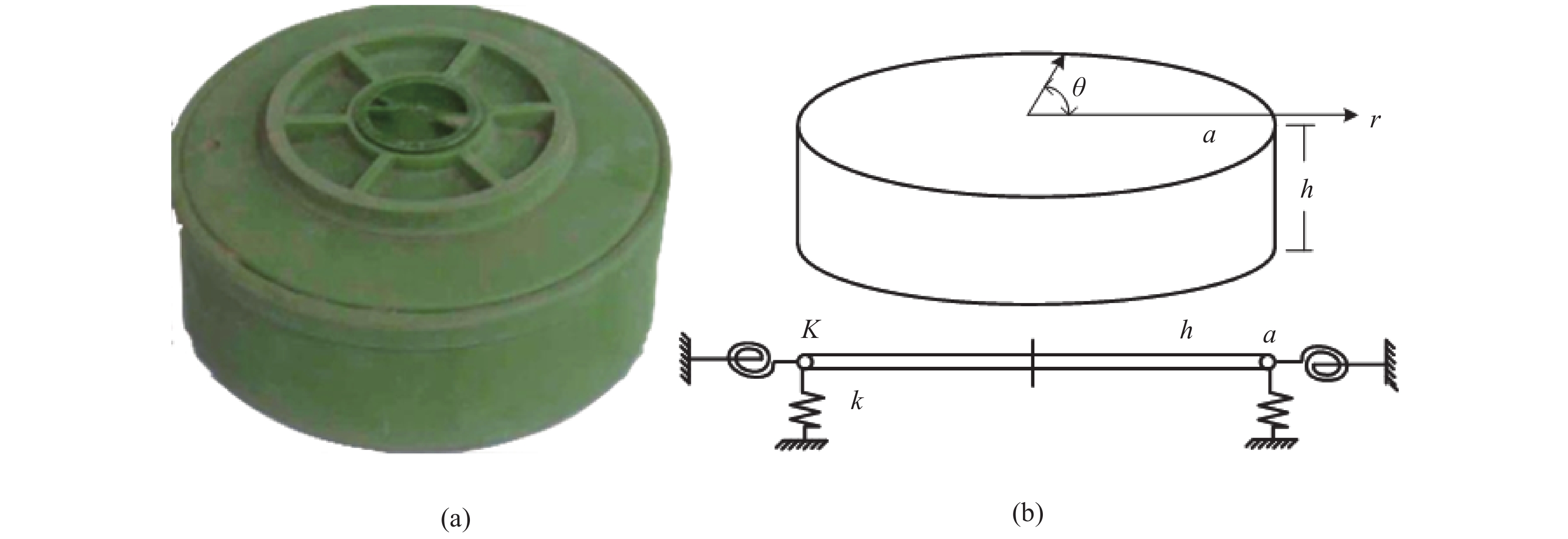
Analysis of the relationship between the mode shapes of a landmine’s upper casing and its laser speckle interference signal
doi: 10.37188/CO.EN.2022-0001
-
摘要:
本文研究了塑壳雷体罩的振型与激光散斑干涉信号之间的映射关系。根据薄圆板的振动方程,建立了地雷上壳体的振型函数。基于激光剪切散斑干涉原理和CCD相机的时间平均法,将振型的离面位移映射到干涉激光的相位。建立的映射关系表明地雷的不同振型对应于独特的贝塞尔条纹。此外,还模拟分析了两种模式的贝塞尔条纹,并进行了实验验证,数值计算和实验结果均验证了理论结论。本文研究为实现声光探雷的快速扫描技术提供了理论依据。
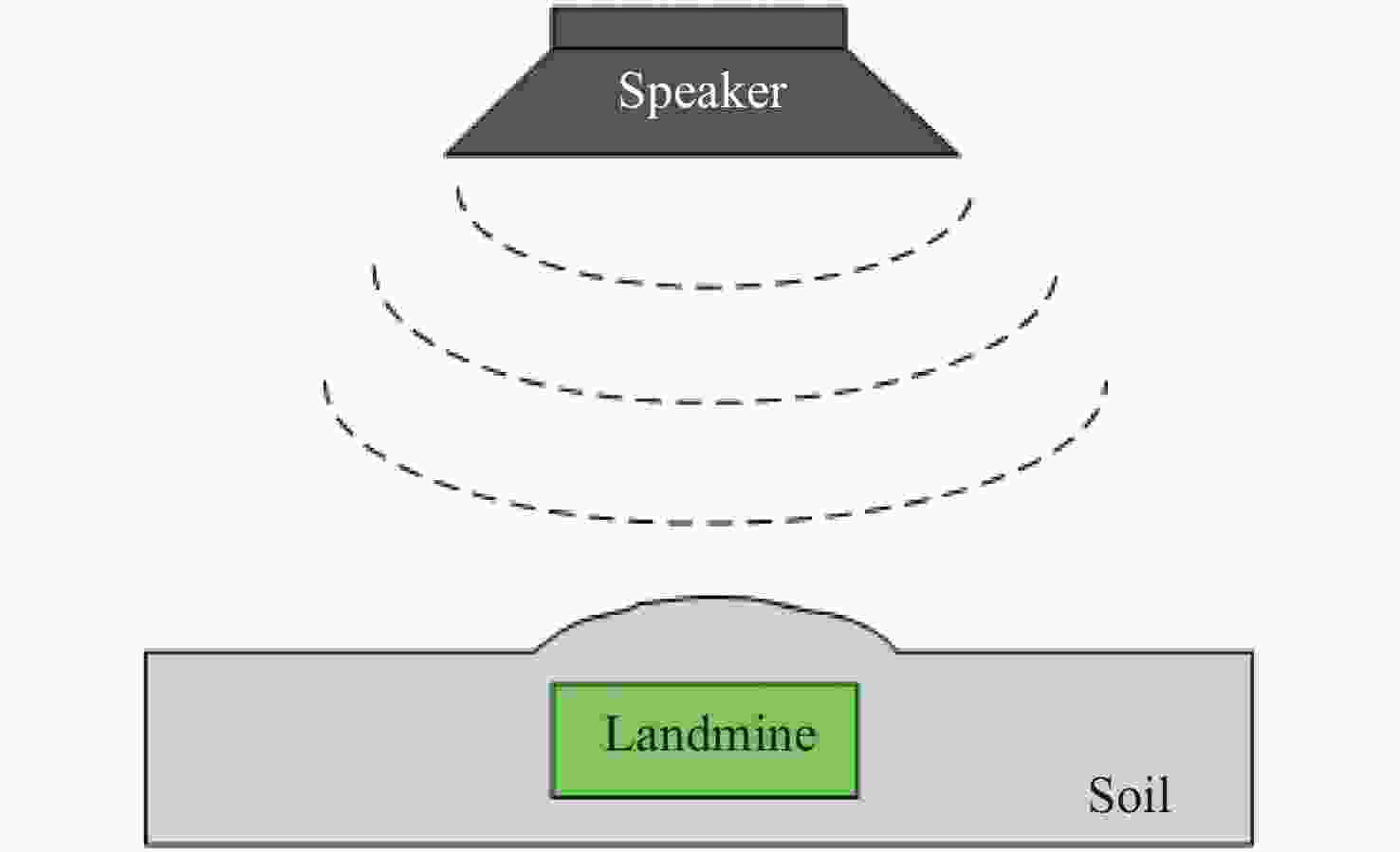
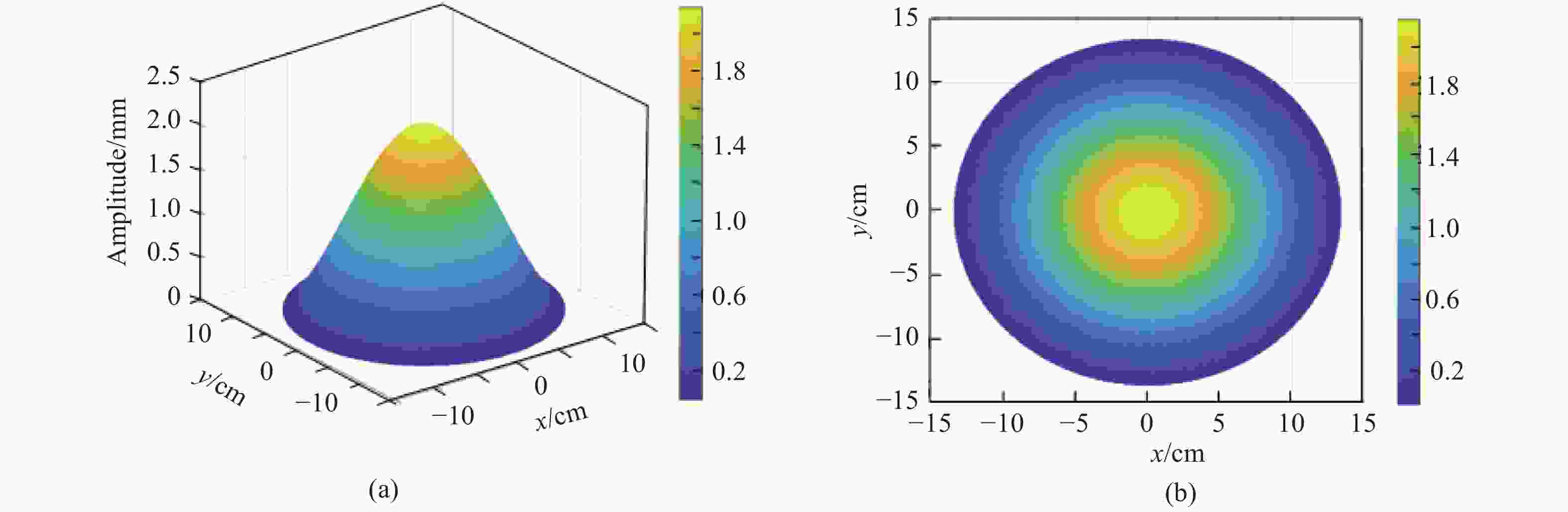
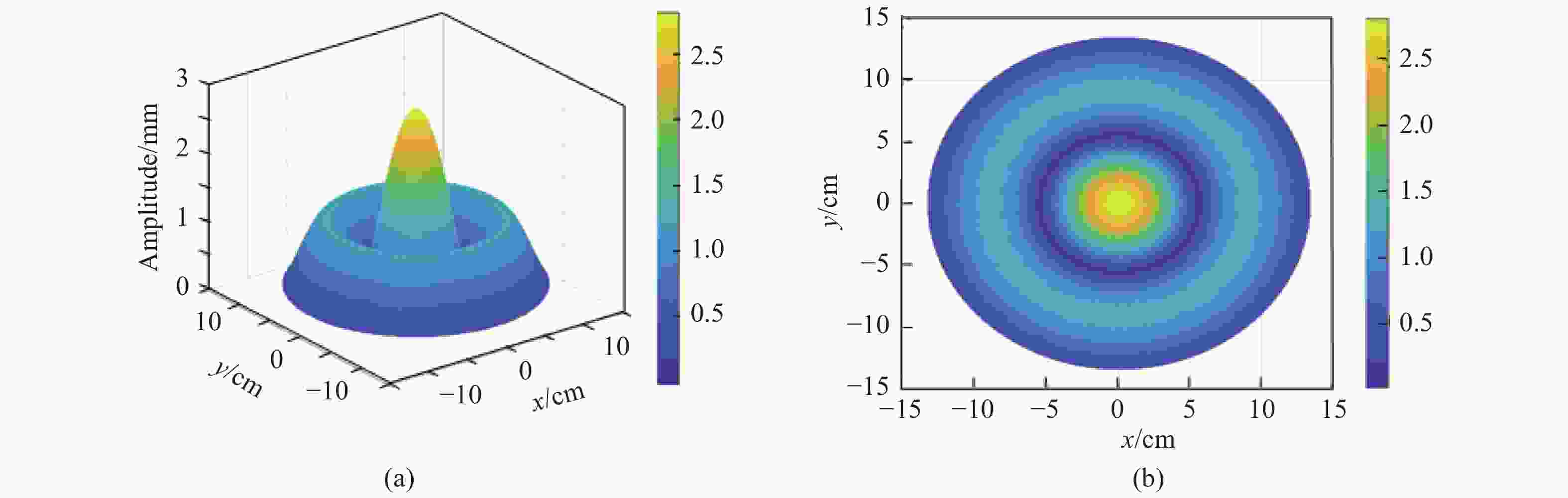
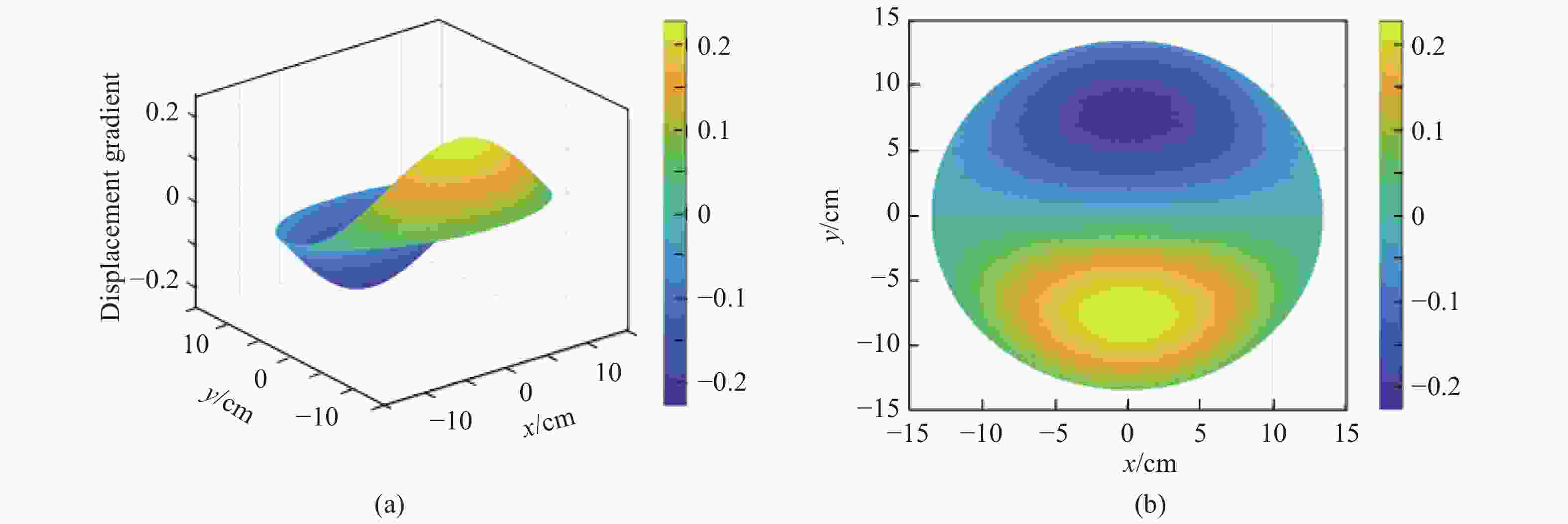
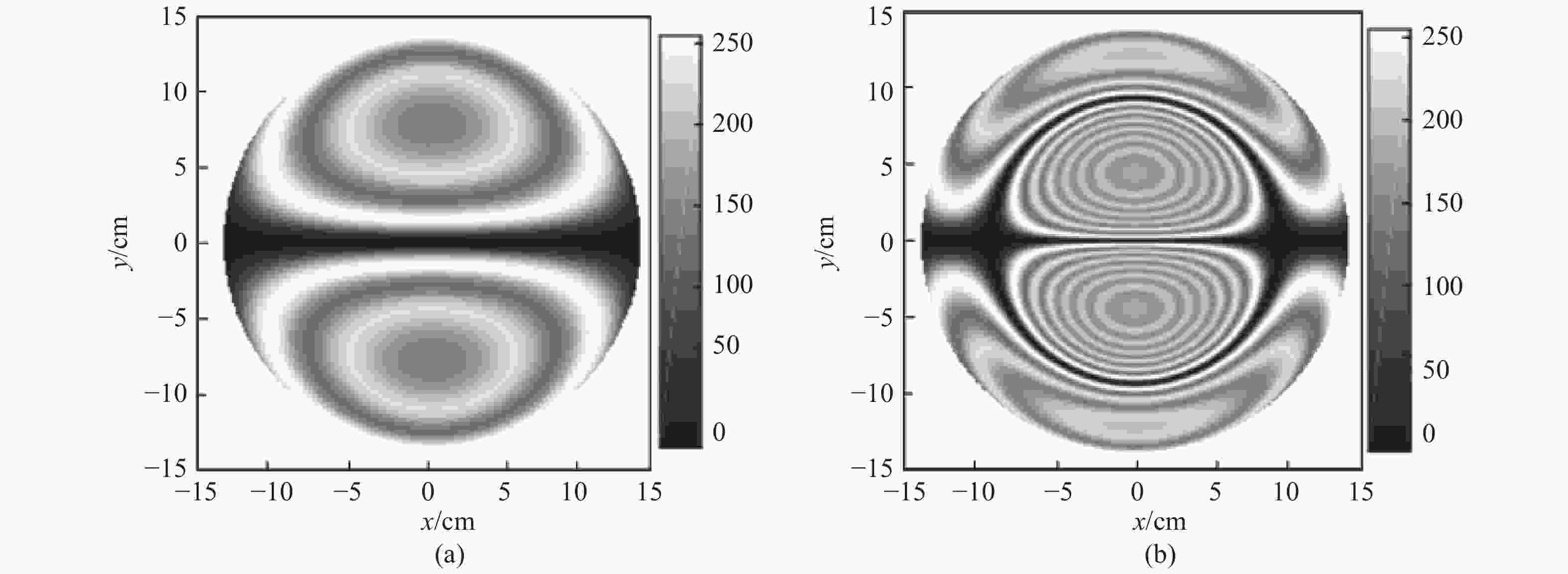
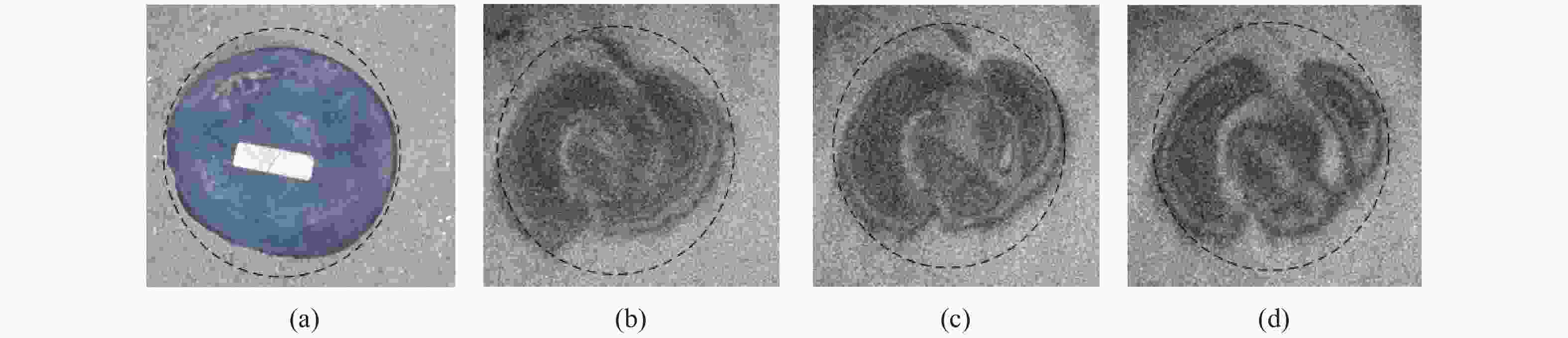
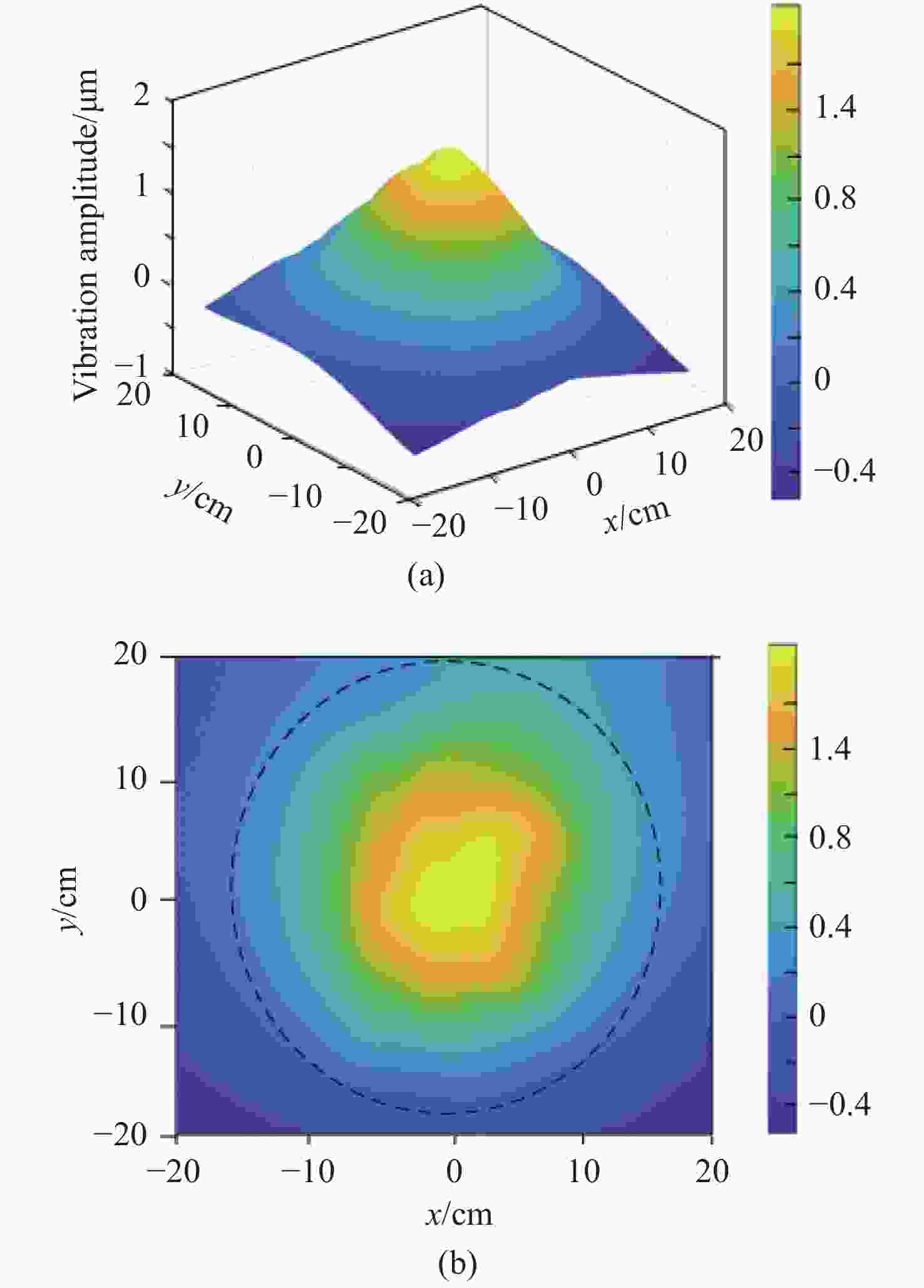
Abstract:The mapping relationship between the mode shapes of a plastic landmine’s upper casing and its laser speckle interference signal was studied. The mode shape function of a landmine’s upper casing is established according to the vibration equation of its thin circular plate. Then, based on the principle of laser shearing speckle interference and the time-average method of a CCD camera, we mapped the out-of-plane displacement of the mode shape to the phase of the interference laser. The study shows that the different mode shapes of the landmine correspond to the unique Bessel fringes. Furthermore, the Bessel fringes of two modes are simulated, and the corresponding experiments were carried out. Both the numerical and experimental results confirm the theoretical conclusions, the research in this paper can provide theoretical evidence for realizing the rapid scanning technology of acoustic-optics landmine detection.
-
Table 1. Simulation parameter setting
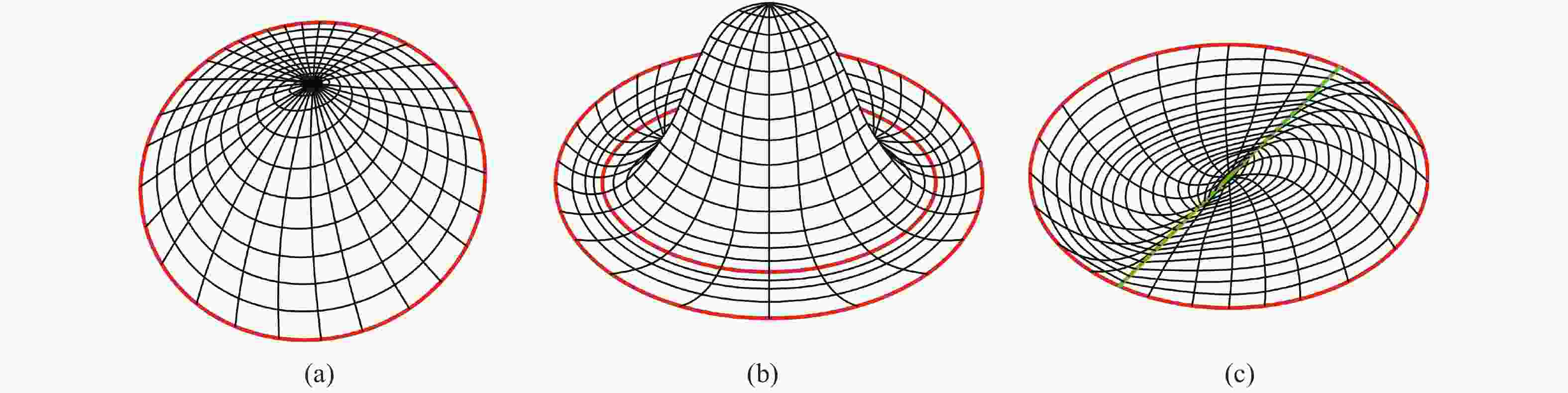
Parameter Simulation settings Transverse stiffness ratio 1000 Poisson’s ratio:$ \upsilon $ 0.33 Young’s modulus: E 17×1019 Pa The radius of the landmine’s upper casing:$ a $ 13.5 cm Laser wavelength:$ \mathrm{\lambda } $ 658 nm Shear amount:$ \delta x $ 6 mm Image size 512×512 Mode (0,1) order, (0,2) order -
[1] WANG CH, MA H, LI J H, et al. Application of laser self-mixing vibration measurement technique in acoustic resonance landmine detection[J]. Optics and Precision Engineering, 2021, 29(4): 710-720. (in Chinese) [2] GUO T, JI M R, SHEN W, et al. The development of international equipments for non-metal landmine detection[J]. Equipment for Geotechnical Engineering, 2010, 11(6): 29-31,28. (in Chinese) doi: 10.3969/j.issn.1009-282X.2010.06.007 [3] POPOV M O, STANKEVICH S A, MOSOV S P, et al. . Landmine detection with UAV-based optical data fusion[C]. IEEE Eurocon 2021-19th International Conference on Smart Technologies, IEEE, 2021: 175-178. [4] KHODOR M, MAKKI I, YOUNES R, et al. Landmine detection in hyperspectral images based on pixel intensity[J]. Remote Sensing Applications:Society and Environment, 2021, 21: 100468. doi: 10.1016/j.rsase.2021.100468 [5] ABEDIN A F Z, IBRAHIM N, ZABIDI N A, et al. The perturbation of backscattered fast neutrons spectrum caused by the resonances of C, N and O for possible use in pyromaterial detection[J]. AIP Conference Proceedings, 2015, 1659(1): 030005. [6] JAMIL A K M, SIVANESAN A, IZAKE E L, et al. Molecular recognition of 2, 4, 6-trinitrotoluene by 6-aminohexanethiol and surface-enhanced Raman scattering sensor[J]. Sensors and Actuators B:Chemical, 2015, 221: 273-280. doi: 10.1016/j.snb.2015.06.046 [7] GILLANDERS R N, GLACKIN J M, BABIĆ Z, et al. Biomonitoring for wide area surveying in landmine detection using honeybees and optical sensing[J]. Chemosphere, 2021, 273: 129646. doi: 10.1016/j.chemosphere.2021.129646 [8] BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498. doi: 10.1063/1.1728759 [9] SABATIER J M, BASS H E, BOLEN L N, et al. Acoustically induced seismic waves[J]. The Journal of the Acoustical Society of America, 1986, 80(2): 646-649. doi: 10.1121/1.394058 [10] SABATIER J M, BASS H E, BOLEN L N, et al. The interaction of airborne sound with the porous ground: the theoretical formulation[J]. The Journal of the Acoustical Society of America, 1986, 79(5): 1345-1352. doi: 10.1121/1.393662 [11] XIANG N, SABATIER J M. An experimental study on antipersonnel landmine detection using acoustic-to-seismic coupling[J]. The Journal of the Acoustical Society of America, 2003, 113(3): 1333-1341. doi: 10.1121/1.1543554 [12] DONSKOY D. Nonlinear seismo-acoustic landmine detection[J]. The Journal of the Acoustical Society of America, 2004, 115(5): 2382. [13] DONSKOY D, REZNIK A, ZAGRAI A, et al. Nonlinear vibrations of buried landmines[J]. The Journal of the Acoustical Society of America, 2005, 117(2): 690-700. doi: 10.1121/1.1850410 [14] ZAGRAI A N, DONSKOY D M, EKIMOV A E. Resonance vibrations of buried landmines[J]. Proceedings of SPIE, 2004, 5415: 21-29. doi: 10.1117/12.540670 [15] ZAGRAI A N, DONSKOY D M, EKIMOV A E. Structural vibrations of buried land mines[J]. The Journal of the Acoustical Society of America, 2005, 118(6): 3619-3628. doi: 10.1121/1.2108754 [16] ALBERTS W, SABATIER J M, WAXLER R. Resonance frequency shift saturation in land mine burial simulation experiments[J]. The Journal of the Acoustical Society of America, 2006, 120(4): 1881-1886. doi: 10.1121/1.2338294 [17] ZHANG Q K, ZHONG SH C, LIN J W, et al. High-performance optical coherence velocimeter: theory and applications[J]. Optics Express, 2019, 27(2): 965-979. doi: 10.1364/OE.27.000965 [18] BURGETT R D, BRADLEY M R, DUNCAN M, et al. Mobile mounted laser Doppler vibrometer array for acoustic landmine detection[J]. Proceedings of SPIE, 2003, 5089: 665-672. doi: 10.1117/12.487186 [19] VALEAU V, SABATIER J, COSTLEY R D, et al. Development of a time-frequency representation for acoustic detection of buried objects[J]. The Journal of the Acoustical Society of America, 2004, 116(5): 2984-2995. doi: 10.1121/1.1806824 [20] WANG CH, DUAN N Y, WU ZH Q, et al. Method for detecting multi-modal vibration characteristics of landmines[J]. Instrumentation, 2018, 5(4): 39-45. [21] WU ZH Q, DUAN N Y, WANG CH, et al. Experimental study on acoustic-to-seismic landmine detection based on laser self-mixing interferometer[J]. Proceedings of SPIE, 2018, 10827: 108271W. [22] RAJESH K R, MURALI R, MOHANACHANDRAN R. Realisation of ultrasonic Doppler Vibrometer array for landmine detection[C]. 2012 IEEE International Ultrasonics Symposium Proceedings, IEEE, 2012: 1027-1030. [23] LI J H, MA H, YANG CH Y, et al. Research progress of the laser vibration measurement techniques for acoustic-to-seismic coupling landmine detection[J]. Chinese Optics, 2021, 14(3): 487-502. doi: 10.37188/CO.2020-0134 [24] LV C C, WANG K F, GU G Q, et al. Accurate full-edge detection and depth measurement of internal defects using digital speckle pattern interferometry[J]. NDT &E International, 2019, 102: 1-8. [25] YAN P ZH, WANG Y H, SUN F Y, et al. Shearography for non-destructive testing of specular reflecting objects using scattered light illumination[J]. Optics &Laser Technology, 2019, 112: 452-457. [26] CHAO J, JING W C, XU T H, et al. Electronic speckle-shearing pattern interferometry for vibration analysis[J]. Nanotechnology and Precision Engineering, 2006, 4(1): 58-62. [27] GOODMAN J W. Introduction to Fourier Optics[M]. New York: The McGraw-Hill Companies, 1968. [28] ZHANG X Q, WANG CH, LI J H, et al. Use of laser speckle shearing interferometric vibration measurement system for acoustic-to-seismic landmine detection[J]. Optical Engineering, 2021, 60(8): 084102. [29] FRANCIS D, TATAM R P, GROVES R M. Shearography technology and applications: a review[J]. Measurement Science and Technology, 2010, 21(10): 102001. doi: 10.1088/0957-0233/21/10/102001 -





 下载:
下载: