Investigation of stimulated Brillouin scattering in As2S3 photonic crystal fibers at the mid-infrared waveband
doi: 10.37188/CO.EN.2022-0003
-
摘要:
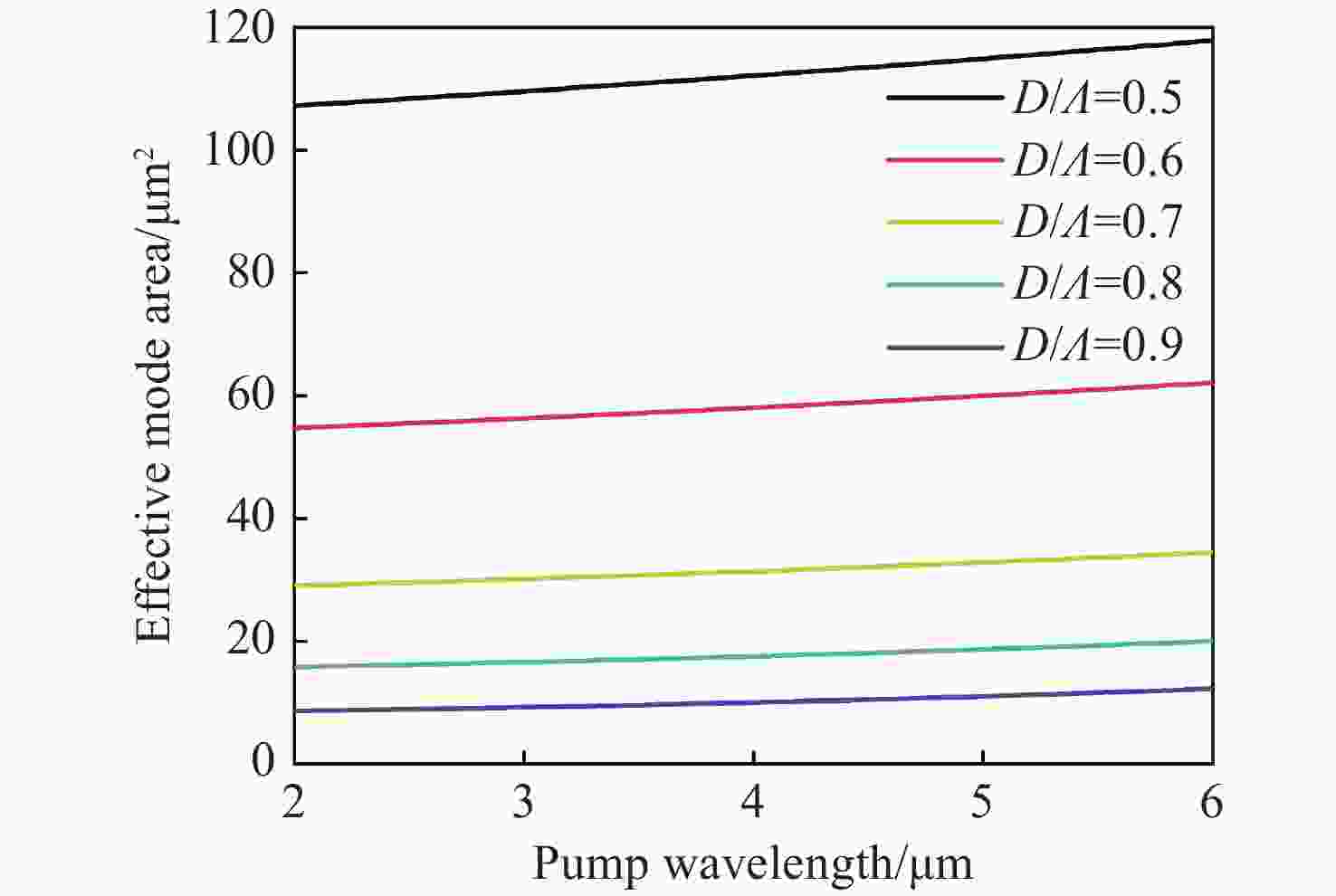
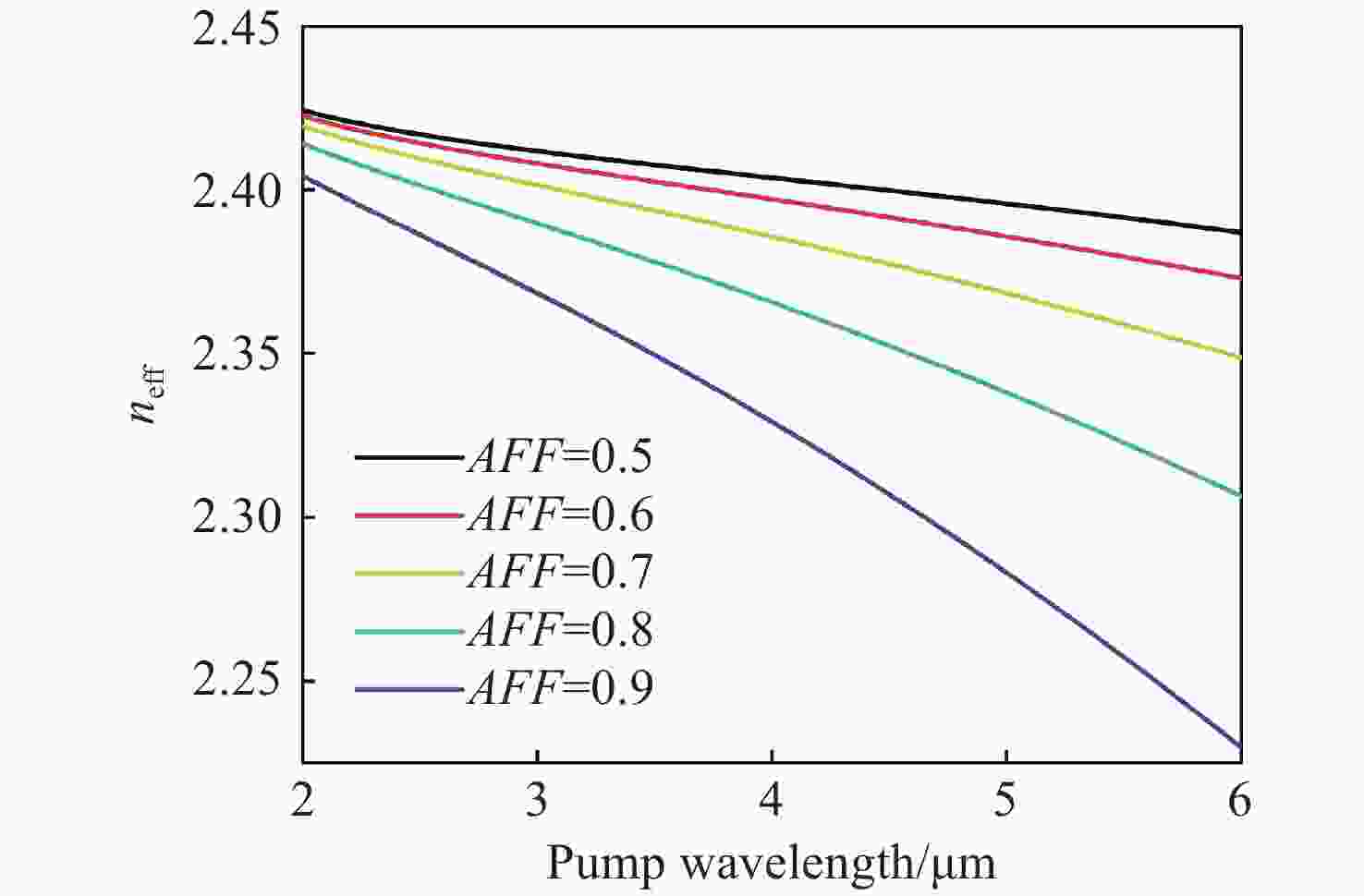
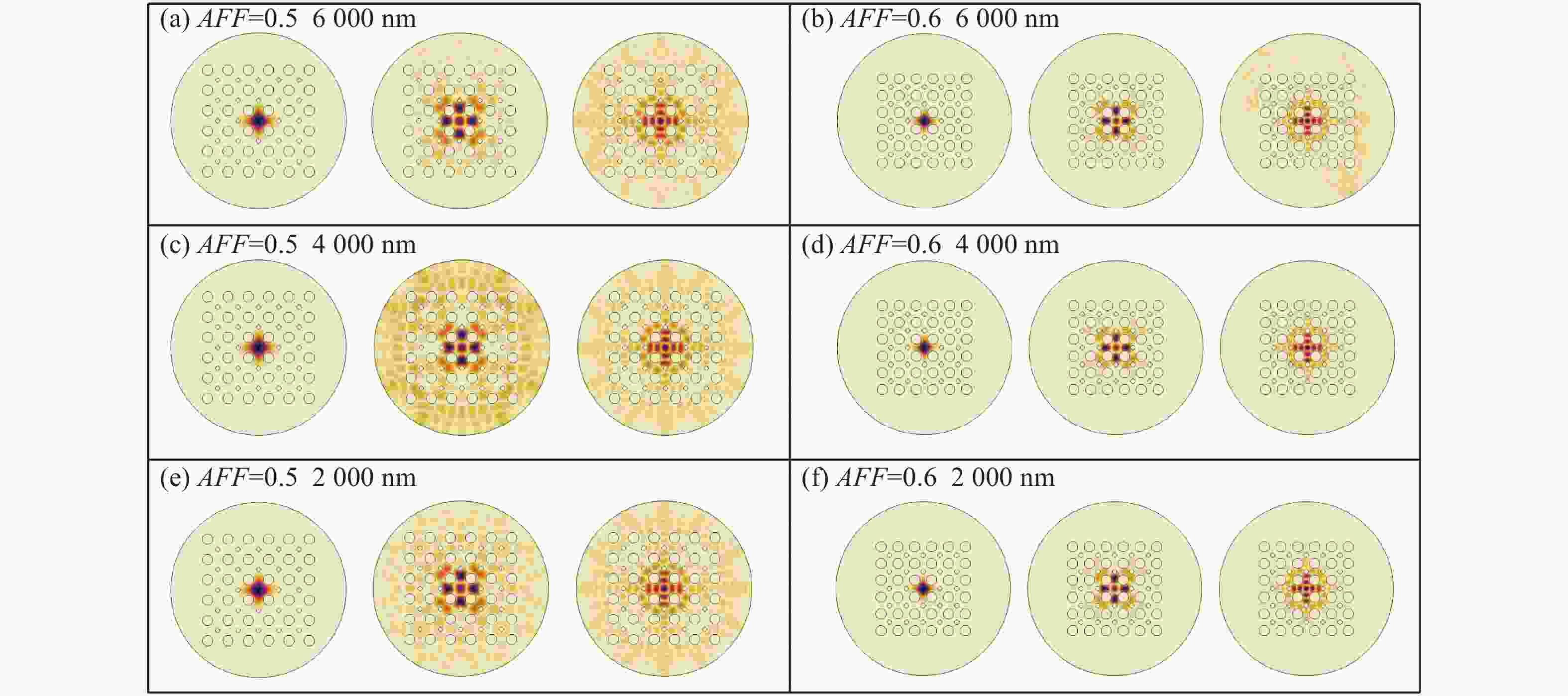
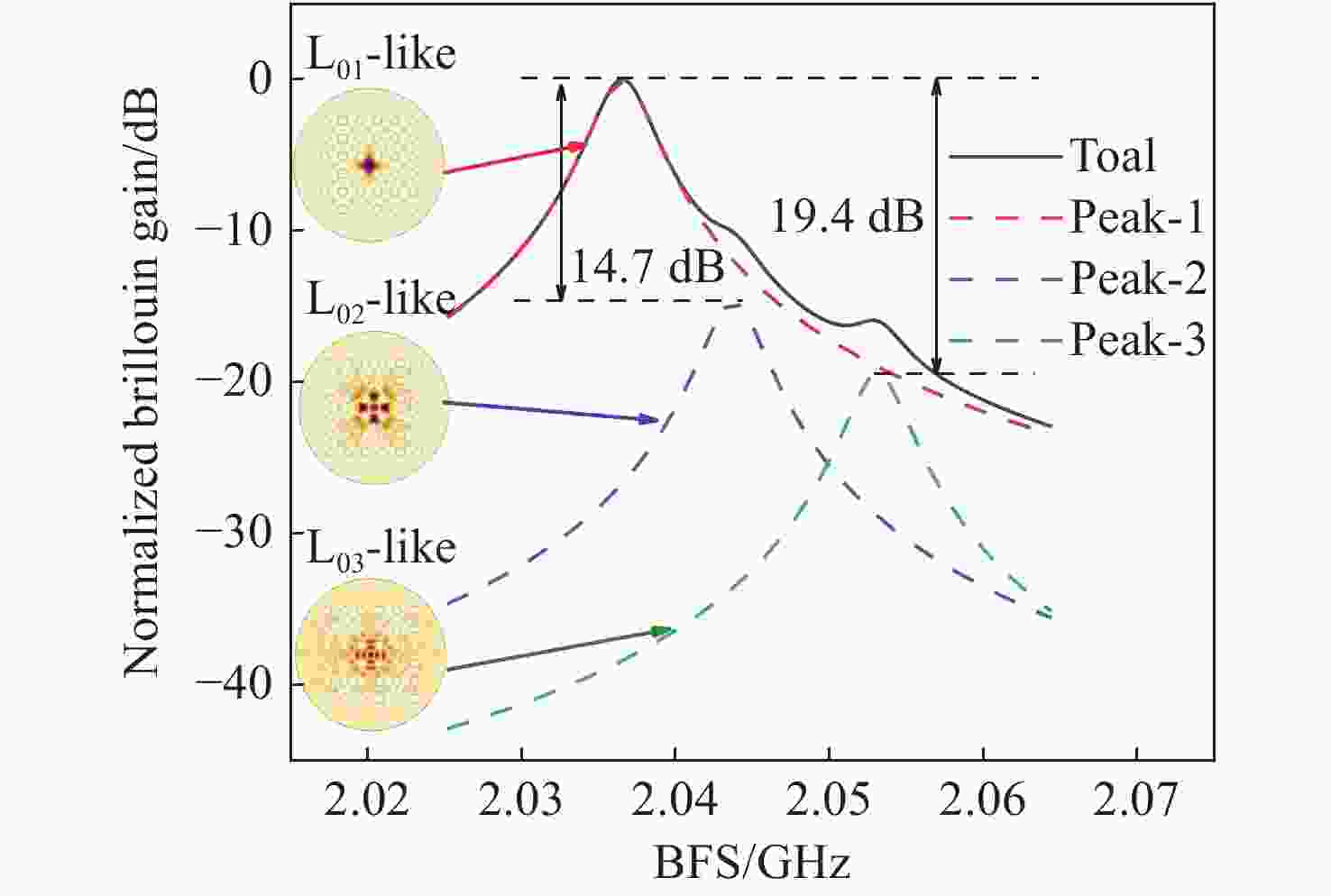
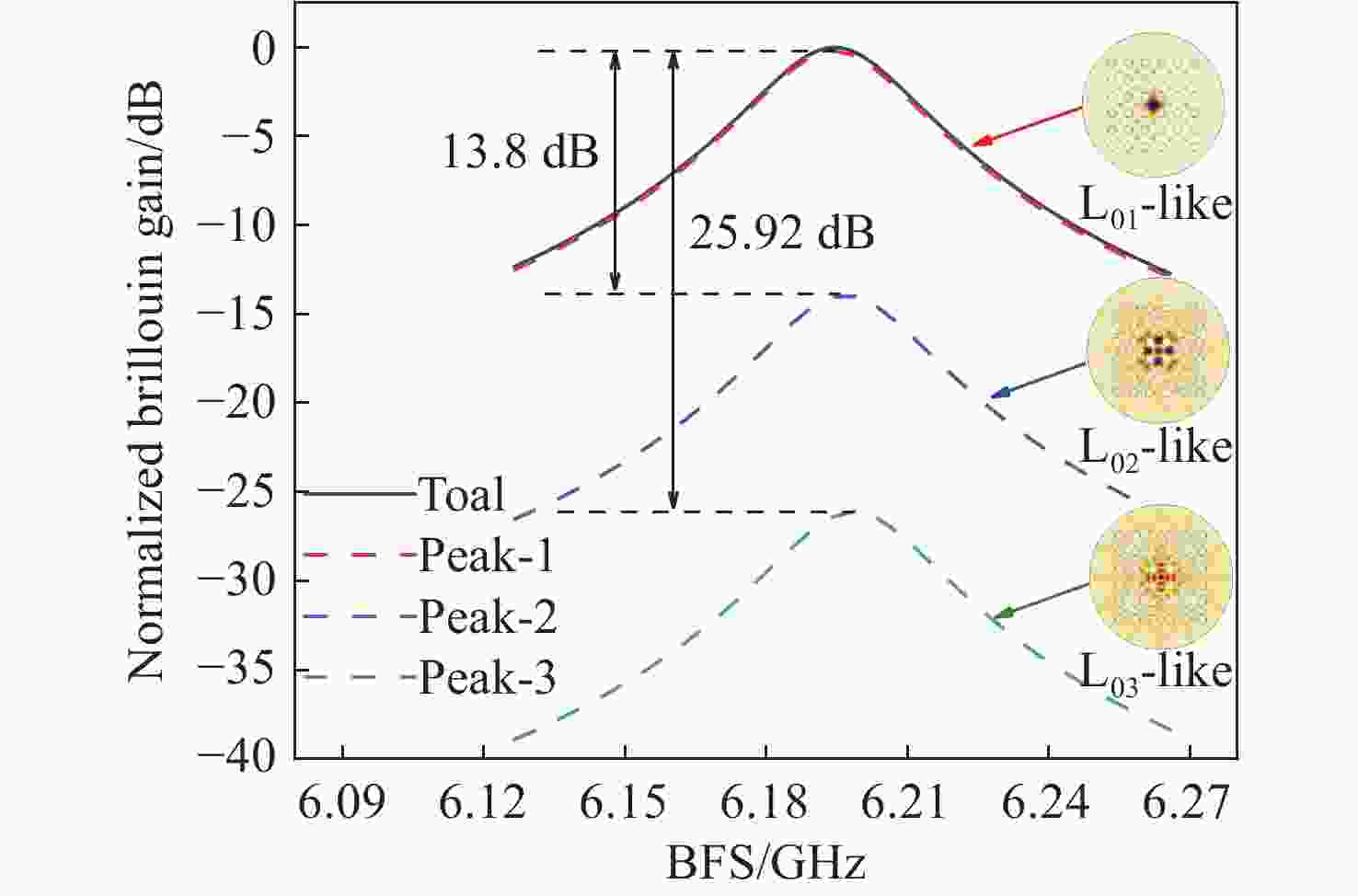
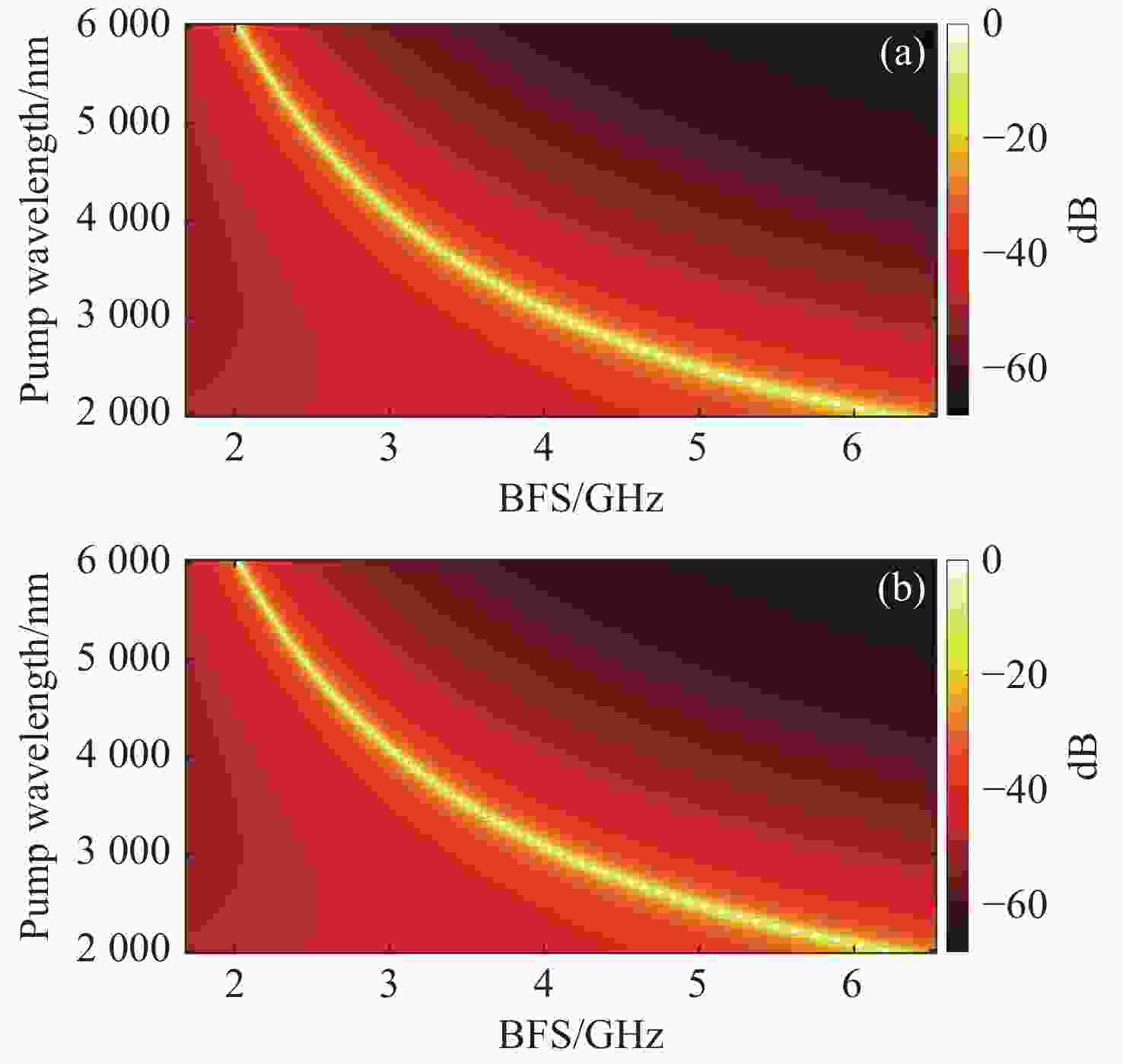
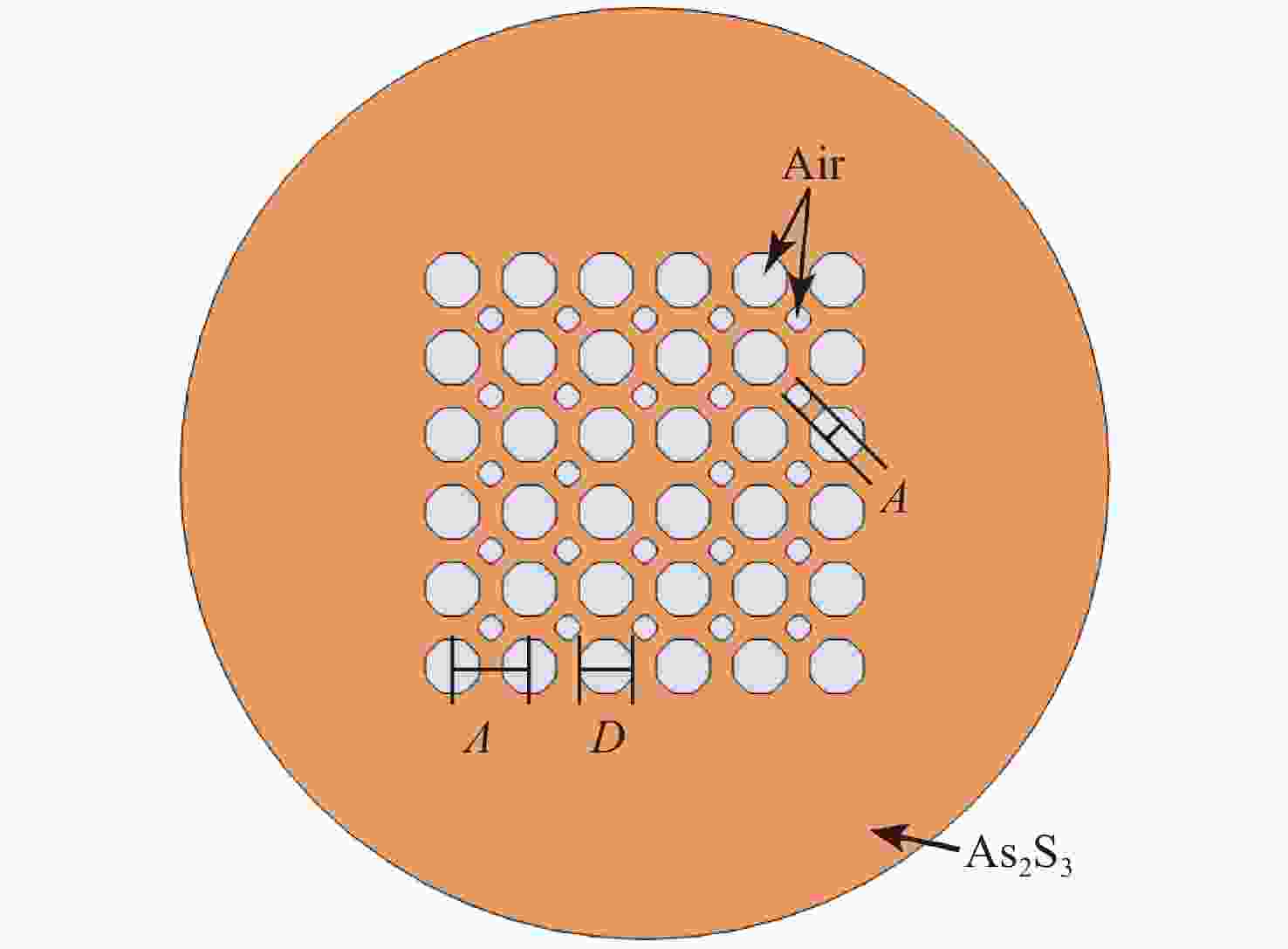
通过有限元方法研究了As2S3光子晶体光纤在2 μm至6 μm波段的受激布里渊散射。数值结果表明,当空气占空比小于0.6时,所提出的光子晶体光纤可保持单模工作。布里渊频移主要受泵浦波长和光纤结构的影响,泵浦波长从2 μm增加到6 μm时,布里渊频移减小了4.16 GHz;而当空气占空比由0.5增加到0.6时,布里渊频移变化量仅为兆赫兹量级。布里渊增益谱的半高全宽取决于声子寿命,泵浦波长为2 μm时布里渊增益谱的半高全宽是泵浦波长为6 μm时的9倍。在空气填充率为0.5和0.6的情况下,提出的光子晶体光纤的最大布里渊增益分别为2.413×10−10 m/W和2.429×10−10 m/W。在光纤有效长度相同的条件下,布里渊阈值与泵浦波长正相关,在空气填充率为0.5和0.6的光子晶体光纤中,使用6 μm泵浦时的布里渊阈值比使用2 μm时分别增大了27.8%和19.6%。这些数值结果对于中红外波段设计和制造基于所提出光纤的光学设备或光学传感器具有重要意义。
Abstract:Stimulated Brillouin scattering in As2S3 photonic crystal fibers was investigated at wavelengths of 2 μm to 6 μm by the finite element method. The numerical results indicate that the proposed photonic crystal fiber can maintain single-mode operation when the air filling factor is less than 0.6. The Brillouin frequency shift is mainly influenced by the pump wavelength and fiber structure. The Brillouin frequency shift decreases by 4.16 GHz when the pump wavelength is increased from 2 μm to 6 μm, while the Brillouin frequency shift changes by the order of megahertz when the rate of air filling increases from 0.5 to 0.6. The FWHM of the Brillouin gain spectrum depends on the phonon lifetime, and the FWHM of the Brillouin gain spectrum is nine times wider at a pump wavelength of 2 μm than that at a pump wavelength of 6 μm. The maximum Brillouin gain of the proposed fibers with air filling fractions of 0.5 and 0.6 are 2.413×10−10 m/W and 2.429×10−10 m/W, respectively. The Brillouin threshold is positively correlated with the pump wavelength for the same effective fiber length, and is 27.8% and 19.6% larger at a pump wavelength of 6 μm than that at 2 μm with air fill factors of 0.5 and 0.6, respectively. The numerical results are of great significance for the design and fabrication of optical devices or optical sensors based on the proposed fibers in the mid-infrared band.
-
Key words:
- stimulated Brillouin scattering /
- mid-infrared /
- photonic crystal fiber /
- fiber optics
-
Table 1. Material parameters of As2S3
Physical property As2S3 Density ρ(kg/m3) 3210 Young modulus Y(GPa) 16.2 Poisson ratio vp 0.285 Photo-elastic tensor p11 0.25 Photo-elastic tensor p12 0.24 Photo-elastic tensor p44 0.005 -
[1] GUAN X, SHI W, RUSCH L A. Ultra-dense wavelength-division multiplexing with microring modulator[J]. Journal of Lightwave Technology, 2021, 39(13): 4300-4306. doi: 10.1109/JLT.2021.3070515 [2] LUBANA A, KAUR S, MALHOTRA Y. Performance optimization of a super-dense wavelength division multiplexing system employing a Raman + erbium–ytterbium doped fiber hybrid optical amplifier[J]. Journal of Optical Technology, 2021, 88(6): 308-314. doi: 10.1364/JOT.88.000308 [3] MA Z Y, WU Q Q, LI Q H, et al. Ultra-dense wavelength division multiplexing passive optical network[J]. Laser &Optoelectronics Progress, 2021, 58(5): 0500006. (in Chinese) [4] ZHANG CH J, GAO M Y, SHI Y, et al. Experimental comparison of orthogonal frequency division multiplexing and universal filter multi-carrier transmission[J]. Journal of Lightwave Technology, 2021, 39(22): 7052-7060. doi: 10.1109/JLT.2021.3113388 [5] XU X Y, YUE D W. Orthogonal frequency division multiplexing modulation techniques in visible light communication[J]. Chinese Optics, 2021, 14(3): 516-527. (in Chinese) doi: 10.37188/CO.2020-0051 [6] ZHU K, ZHOU B, WU H, et al. Multipath distributed acoustic sensing system based on phase-sensitive optical time-domain reflectometry with frequency division multiplexing technique[J]. Optics and Lasers in Engineering, 2021, 142: 106593. doi: 10.1016/j.optlaseng.2021.106593 [7] WU SH Z, WEN H Q, CHEN X H. Method for reducing the influence of crosstalk on quasi-distributed sensing network with time-division multiplexing fibre Bragg gratings[J]. Journal of Physics:Conference Series, 2021, 1754: 012212. doi: 10.1088/1742-6596/1754/1/012212 [8] PEI L, LI ZH Q, WANG J SH, et al. Review on gain equalization technology of fiber amplifier using space division multiplexing[J]. Acta Optica Sinica, 2021, 41(1): 0106001. (in Chinese) doi: 10.3788/AOS202141.0106001 [9] PUTTNAM B J, RADEMACHER G, LUÍS R S. Space-division multiplexing for optical fiber communications[J]. Optica, 2021, 8(9): 1186-1203. doi: 10.1364/OPTICA.427631 [10] DEROH M, BEUGNOT J C, HAMMANI K, et al. Comparative analysis of stimulated Brillouin scattering at 2 µm in various infrared glass-based optical fibers[J]. Journal of the Optical Society of America B, 2020, 37(12): 3792-3800. doi: 10.1364/JOSAB.401252 [11] WANG X, ZHOU P, WANG X L, et al. Tunable slow light via stimulated Brillouin scattering at 2 μm based on Tm-doped fiber amplifiers[J]. Optics Letters, 2015, 40(11): 2584-2587. doi: 10.1364/OL.40.002584 [12] TAO G M, EBENDORFF-HEIDEPRIEM H, STOLYAROV A M, et al. Infrared fibers[J]. Advances in Optics and Photonics, 2015, 7(2): 379-458. doi: 10.1364/AOP.7.000379 [13] ALIMAGHAM F, WINTERBURN J, DOLMAN B, et al. Real-time bioprocess monitoring using a mid-infrared fibre-optic sensor[J]. Biochemical Engineering Journal, 2021, 167: 107889. doi: 10.1016/j.bej.2020.107889 [14] WANG H Y, BAKER C, CHEN L, et al. Stimulated Brillouin scattering in high-birefringence elliptical-core As2Se3-PMMA microfibers[J]. Optics Letters, 2021, 46(5): 945-948. doi: 10.1364/OL.418137 [15] CHEN X Y, YAN X, ZHANG X N, et al. Theoretical investigation of mid-infrared temperature sensing based on four-wave mixing in a CS2-filled GeAsSeTe microstructured optical fiber[J]. IEEE Sensors Journal, 2021, 21(9): 10711-10718. doi: 10.1109/JSEN.2021.3061654 [16] CARCREFF J, CHEVIRÉ F, GALDO E, et al. Mid-infrared hollow core fiber drawn from a 3D printed chalcogenide glass preform[J]. Optical Materials Express, 2021, 11(1): 198-209. doi: 10.1364/OME.415090 [17] XU Q, GAO W Q, LI X, et al. Investigation on optical and acoustic fields of stimulated Brillouin scattering in As2S3 suspended-core microstructured optical fibers[J]. Optik, 2017, 133: 51-59. doi: 10.1016/j.ijleo.2017.01.003 [18] FLOREA C, BASHKANSKY M, DUTTON Z, et al. Stimulated Brillouin scattering in single-mode As2S3 and As2Se3 chalcogenide fibers[J]. Optics Express, 2006, 14(25): 12063-12070. doi: 10.1364/OE.14.012063 [19] VANI P, VINITHA G, NASEER K A, et al. Thulium-doped barium tellurite glasses: structural, thermal, linear, and non-linear optical investigations[J]. Journal of Materials Science:Materials in Electronics, 2021, 32(18): 23030-23046. doi: 10.1007/s10854-021-06787-5 [20] DEROH M, BEUGNOT J C, KIBLER B, et al. . Stimulated Brillouin scattering in Germanium-doped-core optical fibers up to 98% mol doping level[C]. Proceedings of Specialty Optical Fibers 2018, Optica Publishing Group, 2018: SoTu3G. 2. [21] LAMBIN-IEZZI V, LORANGER S, SAAD M, et al. Stimulated Brillouin scattering in SM ZBLAN fiber[J]. Journal of Non-Crystalline Solids, 2013, 359: 65-68. doi: 10.1016/j.jnoncrysol.2012.10.004 [22] SHINKAWA K, ODA Y, MA Z T, et al. Transient stimulated brillouin scattering in multimode As2S3 glass fiber[J]. Japanese Journal of Applied Physics, 2009, 48(7R): 070215. [23] DIOUF M, TRICHLLI A, ZGHAL M. Stimulated Brillouin scattering-based slow light using singlemode As2S3 chalcogenide photonic crystal fiber for temperature sensing[C]. Proceedings of Frontiers in Optics 2019, Optica Publishing Group, 2019: JTu3A. 63. [24] RODNEY W S, MALITSON I H, KING T A. Refractive index of arsenic trisulfide[J]. Journal of the Optical Society of America, 1958, 48(9): 633-636. doi: 10.1364/JOSA.48.000633 [25] WIEDERHECKER G S, DAINESE P, MAYER ALEGRE T P. Brillouin optomechanics in nanophotonic structures[J]. APL Photonics, 2019, 4(7): 071101. doi: 10.1063/1.5088169 [26] TIMOSHENKO S P, GOODIER J N. Theory of Elasticity[M]. New York: McGraw-Hill, 1970. [27] DEMIR H, OZSOY S. Solid-core square-lattice photonic crystal fibers: comparative studies of the single-mode regime and numerical aperture for circular and square air-holes[J]. Optical and Quantum Electronics, 2011, 42(14): 851-862. [28] DASGUPTA S, POLETTI F, LIU SH, et al. Modeling brillouin gain spectrum of solid and microstructured optical fibers using a finite element method[J]. Journal of Lightwave Technology, 2011, 29(1): 22-30. doi: 10.1109/JLT.2010.2091106 [29] AGRAWAL G P. Nonlinear Fiber Optics[M]. 4th ed. Amsterdam: Academic Press, 2007. [30] OGUSU K, LI H P, KITAO M. Brillouin-gain coefficients of chalcogenide glasses[J]. Journal of the Optical Society of America B, 2004, 21(7): 1302-1304. doi: 10.1364/JOSAB.21.001302 -





 下载:
下载: