Phase measurement with dual-frequency grating in a nonlinear system
doi: 10.37188/CO.EN.2022-0013
-
摘要:
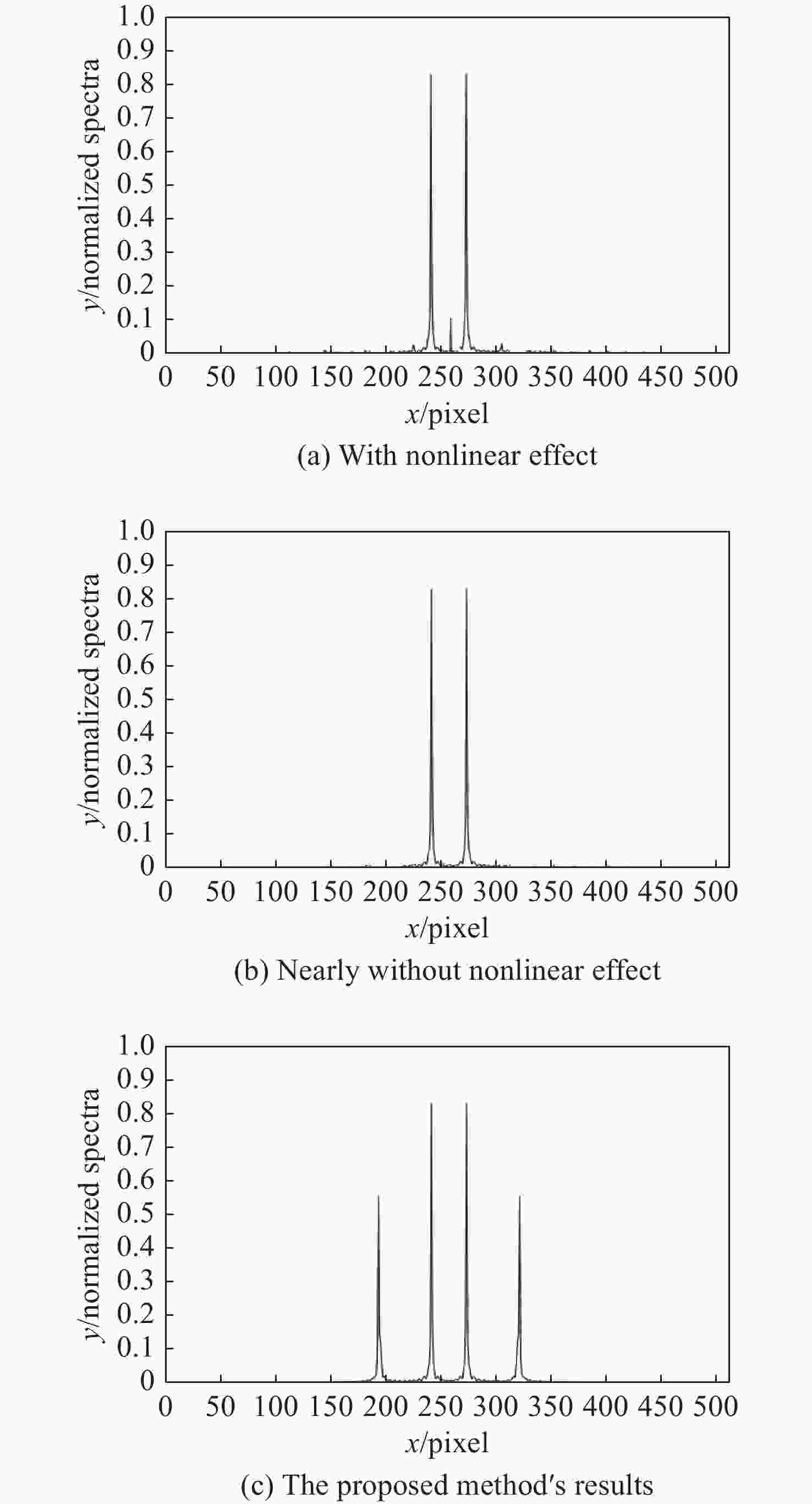
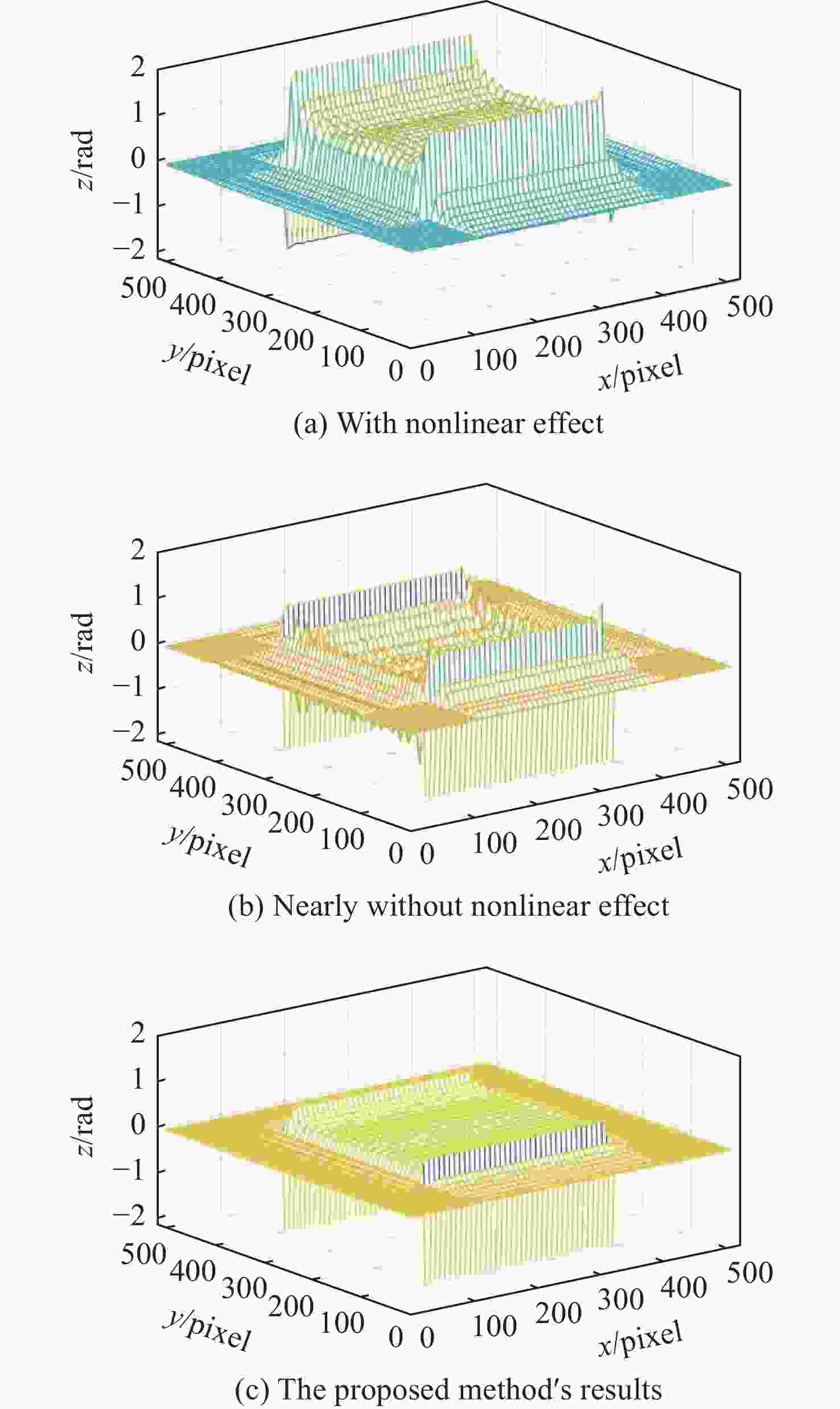
为了在非线性测量系统中获得更好的相位测量结果，提出了一种在几乎消除非线性影响后使用双频光栅投影的相位测量方法。首先，讨论了相位测量系统的非线性效应，分析了频域中存在高阶频谱成份的基本原因，给出了减小非线性效应并分离基频信息的基本方法。然后，在减小系统非线性效应影响的基础上，分析了使用双频光栅投影测量被测物体条纹图像的相位基本原理。为验证所提出的相位测量方法的有效性，进行了计算机仿真和实际实验，获得了良好结果。在仿真实验中，该方法的误差值为有非线性影响方法的27.97%，为几乎没有非线性影响方法的52.51%；在实际实验中，该方法的相位恢复效果最好。表明采用本文方法所测量的相位效果好，误差较小。
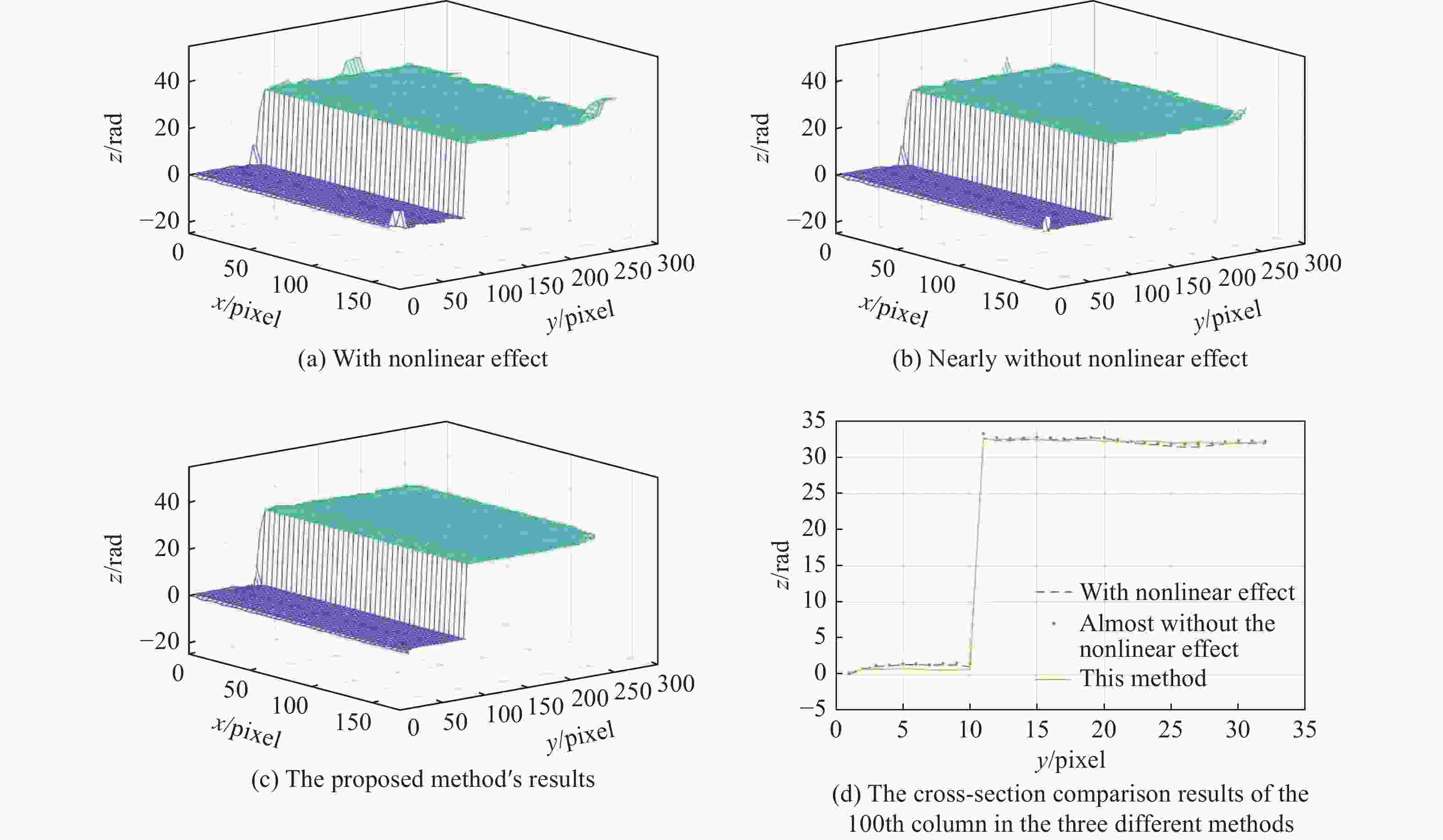
Abstract:To gain better phase measurement results in nonlinear measurement systems, a phase measurement method that uses dual-frequency grating after reducing the nonlinear effect is proposed. Firstly, the nonlinear effect of the phase measurement system is discussed, the basic reason for the existence of high-order spectra components in the frequency domain is analyzed, and the basic method used to reduce the nonlinear effect and separate fundamental frequency information is given. Then, on the basis of reducing the nonlinear effect’s influence on the system, the basic principle of phase measurement for the fringe image of a measured object using the dual-frequency grating method is analyzed. To verify the correctness and effectiveness of the proposed phase measurement method, a computer simulation and a practical experiments were implemented with good results. In the simulation, the error value of this method was 27.97% for the method with nonlinear influence, and 52.51% for that with almost no nonlinear influence. In the experiment, the effect of phase recovery produces the best results. This shows that the proposed phase measurement method is effective with a small error.
-
Key words:
- phase measurement /
- dual-frequency grating /
- system nonlinear effect /
- phase-shift /
- high-order spectra
-
Figure 3. Phase measurement error diagrams gained by three different simulation methods
-
[1] CAI B L, YANG Y, WU J, et al. An improved gray-level coding method for absolute phase measurement based on half-period correction[J]. Optics and Lasers in Engineering, 2020, 128: 106012. doi: 10.1016/j.optlaseng.2020.106012 [2] PENG R J, TIAN M R, XU L, et al. A novel method of generating phase-shifting sinusoidal fringes for 3D shape measurement[J]. Optics and Lasers in Engineering, 2021, 137: 106401. doi: 10.1016/j.optlaseng.2020.106401 [3] HOU Y L, LIANG H G, LI F Q, et al. Spatial-temporal combined phase unwrapping in phase measurement profilometry[J]. Acta Optica Sinica, 2022, 42(1): 0112006. (in Chinese) doi: 10.3788/AOS202242.0112006 [4] QIAO Z K. Study for phase retrieval based on dual frequency grating projection[J]. Optik, 2021, 245: 167668. doi: 10.1016/j.ijleo.2021.167668 [5] ZHANG X, SHAO SH Y, ZHU X, et al. Measurement and calibration of the intensity transform function of the optical 3D profilometry system[J]. Chinese Optics, 2018, 11(1): 123-130. (in Chinese) doi: 10.3788/co.20181101.0123 [6] YIN W, HU Y, FENG SH J, et al. Single-shot 3D shape measurement using an end-to-end stereo matching network for speckle projection profilometry[J]. Optics Express, 2021, 29(9): 13388-13407. doi: 10.1364/OE.418881 [7] XIAO Y SH, CAO Y P, WU Y CH, et al. Single orthogonal sinusoidal grating for gamma correction in digital projection phase measuring profilometry[J]. Optical Engineering, 2013, 52(5): 053605. doi: 10.1117/1.OE.52.5.053605 [8] YE X, CHENG H B, WU H Y, et al. Gamma correction for three-dimensional object measurement by phase measuring profilometry[J]. Optik, 2015, 126(24): 5534-5538. doi: 10.1016/j.ijleo.2015.09.028 [9] YANG Y, HOU Q Y, LI Y, et al. Phase error compensation based on Tree-Net using deep learning[J]. Optics and Lasers in Engineering, 2021, 143: 106628. doi: 10.1016/j.optlaseng.2021.106628 [10] KAMAGARA A, WANG X ZH, LI S K. Towards gamma-effect elimination in phase measurement profilometry[J]. Optik, 2018, 172: 1089-1099. doi: 10.1016/j.ijleo.2018.07.059 [11] LI D L, CAO Y P. 2+1 phase-shifting algorithm based on background correction[J]. Acta Photonica Sinica, 2019, 48(4): 0415001. (in Chinese) doi: 10.3788/gzxb20194804.0415001 [12] QIAO N SH, SUN P. Influence of CCD nonlinearity effect on the three-dimensional shape measurement of dual frequency grating[J]. Chinese Optics, 2021, 14(3): 661-669. (in Chinese) doi: 10.37188/CO.2020-0143 [13] DU M X, YAN Y F, ZHANG R, et al. 3D position angle measurement based on a lens array[J]. Chinese Optics, 2022, 15(1): 45-55. (in Chinese) doi: 10.37188/CO.2021-0129 [14] LI J, SU X Y, GUO L R. Improved Fourier transform profilometry for the automatic measurement of three-dimensional object shapes[J]. Optical Engineering, 1990, 29(12): 1439-1444. doi: 10.1117/12.55746 [15] TAKEDA M, MUTOH K. Fourier transform profilometry for the automatic measurement of 3-D object shapes[J]. Applied Optics, 1983, 22(24): 3977-3982. doi: 10.1364/AO.22.003977 [16] DAI M L, YANG F J, LIU C, et al. A dual-frequency fringe projection three-dimensional shape measurement system using a DLP 3D projector[J]. Optics Communications, 2017, 382: 294-301. doi: 10.1016/j.optcom.2016.08.004 -
下载:
计量
- 文章访问数: 463
- HTML全文浏览量: 331
- PDF下载量: 273
- 被引次数: 0
