同时测试波导传输损耗和弯曲损耗的方法

范作文; 贾连希; 李赵一; 周敬杰; 丛庆宇; 曾宪峰

doi:10.37188/CO.EN.2022-0027

同时测试波导传输损耗和弯曲损耗的方法

范作文^1,,
贾连希^{1, 2, 3, ,},
李赵一¹,
周敬杰¹,
丛庆宇¹,
曾宪峰²

1.
上海大学微电子学院, 上海201800
2.
中国科学院上海微系统与信息研究所, 上海201800
3.
上海新微技术工业研究院, 上海201800

详细信息

中图分类号: TN252
计量
- 文章访问数: 614
- HTML全文浏览量: 350
- PDF下载量: 250
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-27
- 修回日期: 2023-01-30
- 网络出版日期: 2023-04-12

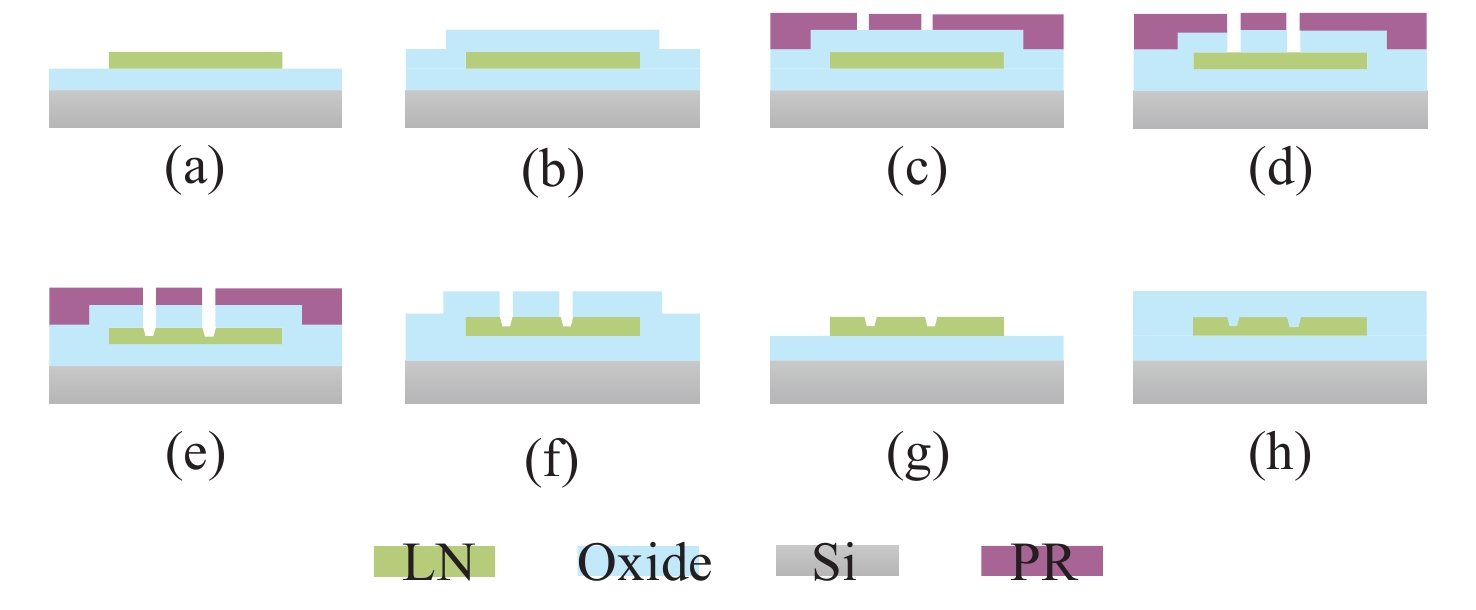
Method for the simultaneous measurement of waveguide propagation loss and bending loss

doi: 10.37188/CO.EN.2022-0027

1.
Microelectronics Institute, Shanghai University, Shanghai 201800, China
2.
Shanghai Institute of Microsystems and Information Technology, Chinese Academy of Sciences, Shanghai 201800, China
3.
Shanghai Industrial μTechnology Research Institute, Shanghai 201800, China

Funds: Supported by the National Key Research and Development Program of China (No. 2018YFB2200500)

More Information

Author Bio:
Fan Zuowen (1998—), male, from Taian, Shandong Province, obtained his bachelors degree from Shandong University of Technology in 2016, and is a postgraduate student in the Microelectronics Institute, Shanghai University. He is mainly engaged in silicon photonics. E-mail: fanzuowen@shu.edu.cn

Jia Lianxi (1982—), male, from Zibo, Shandong Province, professor, obtained a bachelors degree from Shandong University in 2005, and a doctorate degree from the Institute of Semiconductors, Chinese Academy of Sciences in 2010. He is mainly engaged in silicon photonics. E-mail: jialx@mail.sim.ac.cn

Corresponding author: jialx@mail.sim.ac.cn

摘要

摘要:
波导的传输损耗是评价集成光学平台性能的一个关键指标。常用的测量传输损耗的cut-back测试方法需引入弯曲波导测试结构。为了去除弯曲损耗的影响，通常会将弯曲半径设计的足够大，但这样会占用很多的版图面积。本文基于铌酸锂平台提出了一种可以同时测试波导传输损耗和弯曲损耗的方法。通过仿真发现波导弯曲损耗与弯曲半径成指数关系，对弯曲损耗取对数值后，与弯曲半径成线性关系。利用遗传算法拟合cut-back结构的插入损耗曲线，并计算得到波导的传输损耗和弯曲损耗。用该方法测量铌酸锂波导，在1550 nm波长下得到0.558 dB/cm的传输损耗和100 μm弯曲半径下0.698 dB/90°的弯曲损耗。利用这种方法可以同时测试波导的传输损耗和弯曲损耗，还可以大大节省占地面积。
- 传输损耗 /
- 弯曲损耗 /
- 铌酸锂 /
- 遗传算法
Abstract:
The propagation loss of a waveguide is a key indicator to evaluate the performance of an integrated optical platform. The commonly used cut-back method for measuring propagation loss requires the introduction of the spiral test structure. In order to remove bending loss, the bending radius is usually designed to be larger but this consequently has a larger footprint. In this paper, we suggested a method to simultaneously measure the propagation loss and bending loss of waveguides with a cut-back structure. According to simulations, the bending loss can be exponentially fitted with the bending radius, which can be further simplified as linear fitting between the natural logarithm of the bending loss and bending radius. A genetic algorithm was used to fit the insertion loss curve of the cut-back structure and the propagation losses and bending loss were calculated. With this method, we measured a cut-back structure of lithium niobate waveguide and got a propagation loss of 0.558 dB/cm and a bending loss of 0.698 dB/90° at a radius of 100 μm and wavelength of 1550 nm. Using this method, we can simultaneously measure waveguide propagation loss and bending loss while mitigating the footprint.
- propagation loss /
- bending loss /
- lithium niobate /
- genetic algorithm

HTML全文

Figure 1. Process flow of LN waveguide fabrication. (a) LNOI substrate. (b) Deposition of oxide by PECVD. (c) I-line lithography. (d) Hard mask etching. (e) LN etching. (f) Photoresist removal. (g) Hard mask removal. (h) Deposition of cladding by PECVD

下载: 全尺寸图片幻灯片

Figure 2. The SEM image of the fabricated LN waveguide

下载: 全尺寸图片幻灯片

Figure 3. The optical microscope image of the cut-back structure

下载: 全尺寸图片幻灯片

Figure 4. Layout image of the 5 sets of cutback structures for the 5 splits of the grating coupler

下载: 全尺寸图片幻灯片

Figure 5. (a) Simulation of the bending loss of the LN waveguide. The bending loss of the waveguide is exponentially related to the bending radius. (b) The linear fitting of the natural logarithm of the bending loss with the bending radius

下载: 全尺寸图片幻灯片

Figure 6. The basic process of the genetic algorithm

下载: 全尺寸图片幻灯片

Figure 7. The measurement results of the cut-back structure and the fitting results. (a) GC1, (b) GC2, (c) GC3, (d) GC4, (e) GC5-1, (f) GC5-2

下载: 全尺寸图片幻灯片

Table 1. The basic information of the cut-back structure

	Length(cm)	The radius of bend(μm)	Number of radius
WG1	0.1582	100, 110	100×4,110×2
WG2	0.9021	100,110,120,130,140,150	(100-140)×4,150×2
WG3	2.2054	100,110,120…190,200	(100-190) ×4,200×2
WG4	5.2274	100,110,120…290,300	(100-290) ×4,300×2
WG5	11.4854	100,110,120…490,500	(100-490) ×4,500×2

下载: 导出CSV

Table 2. The summary of the fitting results

	α(dB/cm)	α_b0(dB）	k	α_gc(dB)	r
GC1	0.538	0.805	0.0446	20.220	0.072
GC2	0.408	0.698	0.0346	15.448	0.261
GC3	0.558	0.698	0.0399	10.740	0.044
GC4	0.209	0.393	0.0201	12.114	0.366
GC5-1	0.194	0.416	0.0176	35.350	0.355
GC5-2	0.421	0.339	0.0194	29.666	0.230

下载: 导出CSV

Table 3. The performance comparison of different measurement methods

	Advantages	Disadvantages
Traditional cut-back^[33]	Widely employed owing to its ease of use.	Can’t simultaneously measure the propagation loss and bending loss; Requires identical coupling conditions.
Three-prism Method^[34]	Does not require constant coupling conditions	Has low measurement accuracy.
Fabry-Perot transmission method^[35]	Can eliminate the influence of coupling loss and has higher accuracy	Requires a complex coupling system.
This paper	Can simultaneously measure waveguide propagation loss and bending loss; Smaller footprint; Simple and convenient operation.

下载: 导出CSV

参考文献(35)

[1]	ARIZMENDI L. Photonic applications of lithium niobate crystals[J]. Physica Status Solidi (A), 2004, 201(2): 253-283. doi: 10.1002/pssa.200303911
[2]	WEIS R S, GAYLORD T K. Lithium niobate: summary of physical properties and crystal structure[J]. Applied Physics A, 1985, 37(4): 191-203. doi: 10.1007/BF00614817
[3]	WU R B, WANG M, XU J, et al.. Long low-loss-litium niobate on insulator waveguides with sub-nanometer surface roughness[J]. Nanomaterials, 2018, 8(11): 910. doi: 10.3390/nano8110910
[4]	ZHU D, SHAO L B, YU M J, et al.. Integrated photonics on thin-film lithium niobate[J]. Advances in Optics and Photonics, 2021, 13(2): 242-352. doi: 10.1364/AOP.411024
[5]	RABIEI P, GUNTER P. Optical and electro-optical properties of submicrometer lithium niobate slab waveguides prepared by crystal ion slicing and wafer bonding[J]. Applied Physics Letters, 2004, 85(20): 4603-4605. doi: 10.1063/1.1819527
[6]	POBERAJ G, HU H, SOHLER W, et al.. Lithium niobate on insulator (LNOI) for micro-photonic devices[J]. Laser & Photonics Reviews, 2012, 6(4): 488-503.
[7]	LEVY M, RADOJEVIC A M. Single-crystal lithium niobate films by crystal ion slicing[M]//ALEXE M, GÖSELE U. Wafer Bonding: Applications and Technology. Berlin: Springer, 2004: 417-450.
[8]	ZHANG M, BUSCAINO B, WANG CH, et al.. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator[J]. Nature, 2019, 568(7752): 373-377. doi: 10.1038/s41586-019-1008-7
[9]	XU M Y, HE M B, ZHANG H G, et al.. High-performance coherent optical modulators based on thin-film lithium niobate platform[J]. Nature Communications, 2020, 11(1): 3911. doi: 10.1038/s41467-020-17806-0
[10]	WANG CH, ZHANG M, CHEN X, et al.. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages[J]. Nature, 2018, 562(7725): 101-104. doi: 10.1038/s41586-018-0551-y
[11]	WANG CH, LANGROCK C, MARANDI A, et al.. Ultrahigh-efficiency wavelength conversion in nanophotonic periodically poled lithium niobate waveguides[J]. Optica, 2018, 5(11): 1438-1441. doi: 10.1364/OPTICA.5.001438
[12]	LIN J T, YAO N, HAO ZH ZH, et al.. Broadband quasi-phase-matched harmonic generation in an on-chip monocrystalline lithium niobate microdisk resonator[J]. Physical Review Letters, 2019, 122(17): 173903. doi: 10.1103/PhysRevLett.122.173903
[13]	HE M B, XU M Y, REN Y X, et al.. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s⁻¹ and beyond[J]. Nature Photonics, 2019, 13(5): 359-364. doi: 10.1038/s41566-019-0378-6
[14]	CAI L T, KONG R R, WANG Y W, et al.. Channel waveguides and y-junctions in x-cut single-crystal lithium niobate thin film[J]. Optics Express, 2015, 23(22): 29211-29221. doi: 10.1364/OE.23.029211
[15]	CAI L T, WANG Y W, HU H. Low-loss waveguides in a single-crystal lithium niobate thin film[J]. Optics Letters, 2015, 40(13): 3013-3016. doi: 10.1364/OL.40.003013
[16]	HU H, YANG J, GUI L, et al.. Lithium niobate-on-insulator (LNOI): status and perspectives[J]. Proceedings of SPIE, 2012, 8431: 84311D.
[17]	KRASNOKUTSKA I, TAMBASCO J L J, LI X J, et al.. Ultra-low loss photonic circuits in lithium niobate on insulator[J]. Optics Express, 2018, 26(2): 897-904. doi: 10.1364/OE.26.000897
[18]	ULLIAC G, COURJAL N, CHONG H M H, et al.. Batch process for the fabrication of LiNbO₃ photonic crystals using proton exchange followed by CHF₃ reactive ion etching[J]. Optical Materials, 2008, 31(2): 196-200. doi: 10.1016/j.optmat.2008.03.004
[19]	DONG P, QIAN W, LIAO SH R, et al.. Low loss shallow-ridge silicon waveguides[J]. Optics Express, 2010, 18(14): 14474-14479. doi: 10.1364/OE.18.014474
[20]	GUTIERREZ A M, BRIMONT A, AAMER M, et al.. Method for measuring waveguide propagation losses by means of a Mach–Zehnder Interferometer structure[J]. Optics Communications, 2012, 285(6): 1144-1147. doi: 10.1016/j.optcom.2011.11.064
[21]	TAEBI S, KHORASANINEJAD M, SAINI S S. Modified fabry-perot interferometric method for waveguide loss measurement[J]. Applied Optics, 2008, 47(35): 6625-6630. doi: 10.1364/AO.47.006625
[22]	HE Y M, LI ZH S, LU D. A waveguide loss measurement method based on the reflected interferometric pattern of a Fabry-Perot cavity[J]. Proceedings of SPIE, 2018, 10535: 105351U.
[23]	HOLLAND J H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence[M]. Cambridge: The MIT Press, 1992.
[24]	ALONSO J M, ALVARRUIZ F, DESANTES J M, et al.. Combining neural networks and genetic algorithms to predict and reduce diesel engine emissions[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(1): 46-55. doi: 10.1109/TEVC.2006.876364
[25]	VERMA R, LAKSHMINIARAYANAN P A. A case study on the application of a genetic algorithm for optimization of engine parameters[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2006, 220(4): 471-479.
[26]	BAHADORI M, NIKDAST M, CHENG Q X, et al.. Universal design of waveguide bends in silicon-on-insulator photonics platform[J]. Journal of Lightwave Technology, 2019, 37(13): 3044-3054. doi: 10.1109/JLT.2019.2909983
[27]	THYAGARAJAN K, SHENOY M R, GHATAK A K. Accurate numerical method for the calculation of bending loss in optical waveguides using a matrix approach[J]. Optics Letters, 1987, 12(4): 296-298. doi: 10.1364/OL.12.000296
[28]	HAN ZH H, ZHANG P, BOZHEVOLNYI S I. Calculation of bending losses for highly confined modes of optical waveguides with transformation optics[J]. Optics Letters, 2013, 38(11): 1778-1780. doi: 10.1364/OL.38.001778
[29]	STENGER V E, TONEY J, PONICK A, et al. Low loss and low vpi thin film lithium niobate on quartz electro-optic modulators[C]. 2017 European Conference on Optical Communication (ECOC), IEEE, 2017: 1-3.
[30]	LI X P, CHEN K X, HU ZH F. Low-loss bent channel waveguides in lithium niobate thin film by proton exchange and dry etching[J]. Optical Materials Express, 2018, 8(5): 1322-1327. doi: 10.1364/OME.8.001322
[31]	REN T H, ZHANG M, WANG CH, et al.. An integrated low-voltage broadband lithium niobate phase modulator[J]. IEEE Photonics Technology Letters, 2019, 31(11): 889-892. doi: 10.1109/LPT.2019.2911876
[32]	DING T T, ZHENG Y L, CHEN X F. On-chip solc-type polarization control and wavelength filtering utilizing periodically poled lithium niobate on insulator ridge waveguide[J]. Journal of Lightwave Technology, 2019, 37(4): 1296-1300. doi: 10.1109/JLT.2019.2892317
[33]	VLASOV Y A, MCNAB S J. Losses in single-mode silicon-on-insulator strip waveguides and bends[J]. Optics Express, 2004, 12(8): 1622-1631. doi: 10.1364/OPEX.12.001622
[34]	WON Y H, JAUSSAUD P C, CHARTIER G H. Three-prism loss measurements of optical waveguides[J]. Applied Physics Letters, 1980, 37(3): 269-271. doi: 10.1063/1.91903
[35]	REGENER R, SOHLER W. Loss in low-finesse Ti: LiNbO₃ optical waveguide resonators[J]. Applied Physics B, 1985, 36(3): 143-147.