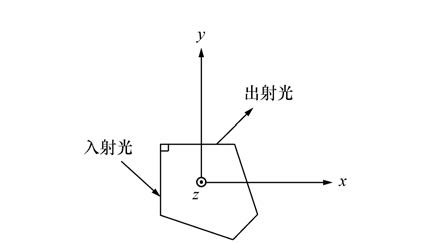
Changes of output light's angles with pentaprism rotation
-
摘要: 为了对大口径平面镜面形轮廓的五棱镜扫描法测试进行误差分析和修正,对五棱镜转动时出射光角度的变化进行了分析与精确计算。首先建立了合适的坐标系并规定了角度的正负,然后由入射光的偏摆角和俯仰角计算入射光向量,接着介绍了五棱镜的作用矩阵与坐标转换矩阵,在此基础上详细分析了五棱镜转动的整个过程并且计算了出射光向量。然后计算出射光的偏摆角和俯仰角,再计算当五棱镜没有转动时出射光的偏摆角和俯仰角。最后计算出射光偏摆角和俯仰角的变化。特别分析了当入射光垂直入射五棱镜的情况。随后进行了实际计算与实验,总结了出射光角度变化的一些规律。将计算数据与实验数据进行了比较,结果最大偏差为1"。最大偏差在实验精度范围内,证明了计算方法是正确的。Abstract: In order to analyse and correct the measurement errors of a large flat mirror's surface profile by using a scanning pentaprism, the changes of the output light's angles with the pentaprism rotation are analysed and calculated accurately. First, a suitable coordinate system is built and the signs of angles are fixed. Then, the input light vector is calculated from the input light's yaw angle and pitch angle. The function matrix of the pentaprism and the coordinate transformation matrix are introduced. The whole process of the pentaprism rotation is analysed in detail and the output light vector is calculated on the basis of above. Then the output light's yaw angle and pitch angle are calculated. The output light's yaw angle and pitch angle without pentaprism rotation are calculated. Last, the changes of the output light's yaw angle and pitch angle are calculated. The situation is analysed specially when the input light is perpendicular incident into the pentaprism. The actual calculation and experiment are carried out and some disciplinarians of the changes of the output light's angles are summarized. The calculation data are compared with the experiment data, and the largest deviation is 1" which is within the range of experiment accuracy, indicating that the calculation method is right.
-
Key words:
- flat mirror measurement /
- pentaprism /
- rotation /
- change of angle
-
表 1 五棱镜绕x轴转动时出射光角度的变化量(计算值)
Table 1. Changes of output light′s angles when pentaprism rotates around x axis(from calculation)
表 2 五棱镜绕y轴转动时出射光角度的变化量(计算值)
Table 2. Changes of output light′s angles when pentaprism rotates around y axis(from calculation)
表 3 五棱镜绕x轴转动时出射光角度的变化量(实验值)
Table 3. Changes of output light′s angles when pentaprism rotates around x axis(from experiment)
表 4 五棱镜绕y轴转动时出射光角度的变化量(实验值)
Table 4. Changes of output light′s angles when pentaprism rotates around y axis(from experiment)
表 5 五棱镜绕z轴转动时出射光角度的变化量(实验值)
Table 5. Changes of output light′s angles when pentaprism rotates around z axis(from experiment)
-
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] -






 下载:
下载: