航空相机镜间快门对像移的影响分析

于春风; 陈志超; 贾平; 王乃详; 候汉

doi:10.3788/CO.2019-0127

航空相机镜间快门对像移的影响分析

于春风^{1, 2, ,},
陈志超^{1, 2,},
贾平^{1, 2,},
王乃详^{1, 2},
候汉^{1, 2}

1.
中国科学院长春光学精密机械与物理研究所吉林长春 130033
2.
中国科学院航空光学成像与测量重点实验室吉林长春 130033

详细信息

中图分类号: TP73
计量
- 文章访问数: 2024
- HTML全文浏览量: 789
- PDF下载量: 94
- 被引次数: 0
出版历程
- 收稿日期: 2019-06-18
- 修回日期: 2019-06-28
- 刊出日期: 2020-06-01

Analysis of the effect of lens shutter on image motion in aerial camera

doi: 10.3788/CO.2019-0127

YU Chun-feng^{1, 2
, ,},
CHEN Zhi-chao^{1, 2
,},
JIA Ping^{1, 2
,},
WANG Nai-xiang^{1, 2},
HOU Han^{1, 2}

1.
Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China
2.
Key Laboratory of Airborne Optical Imaging and Measurement, Chinese Academy of Sciences, Changchun 130033, China

Funds: Supported by National Key R&D Program Funding Projects（No. 2016YFC0803000）

More Information

Author Bio:
YU Chun-feng (1979—), was born in Changchun, Jilin province. In 2013, he graduated from University of Chinese Academy of Sciences. Now he is working as an associate professor at Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences. His research interests are aerial imaging and measurement technology. E-mail: hou791016@163.com

CHEN Zhi-chao (1979-), was born in Tieling, Liaoning province, Doctor, associate professor, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences. In 2016,graduated from University of Chinese Academy of Sciences, He research interests are automatic focusing technology of aerial camera. E-mail: 17522332@qq.com

JIA Ping (1964-), Doctor, professor, Ph.D.supervisor, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences. He research interests are aerial imaging and measuring instrument technology. E-mail: jiap@ciomp,ac,cn

Corresponding author: hou791016@163.com

摘要

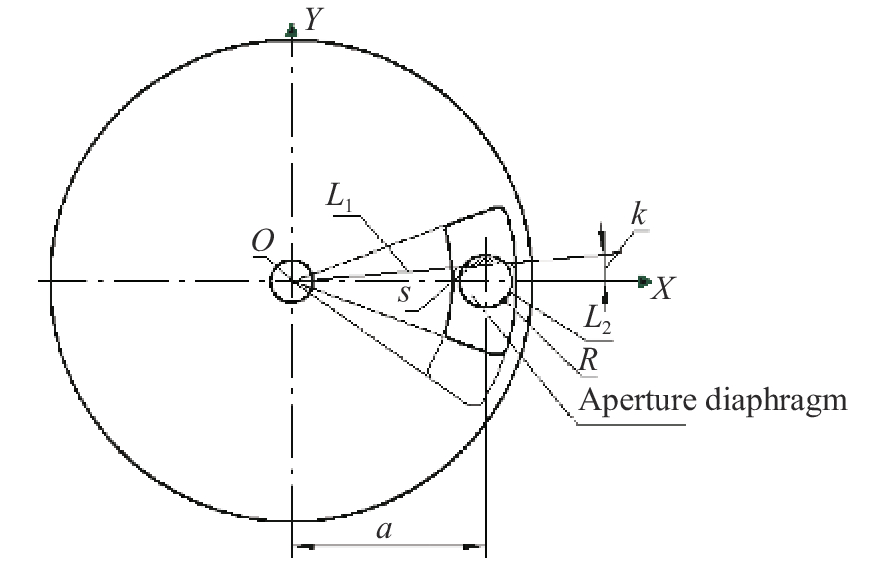
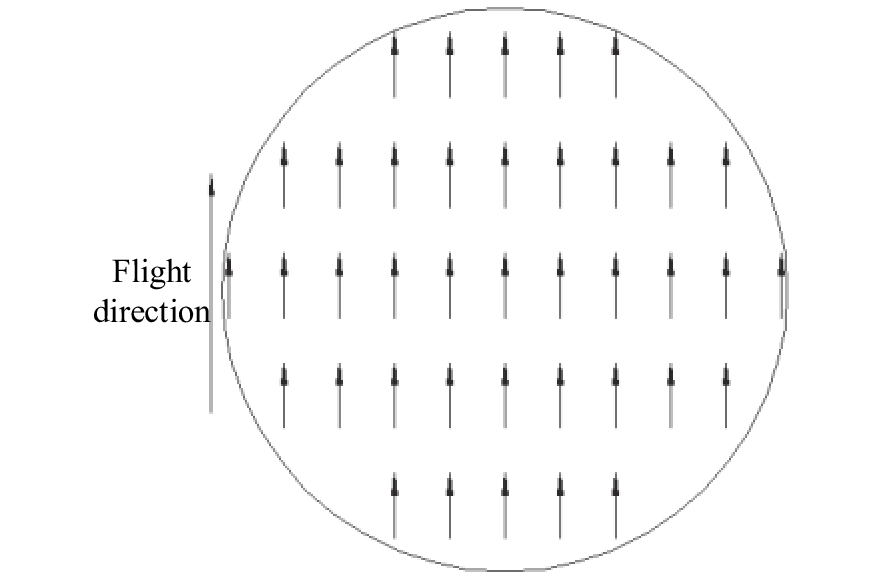
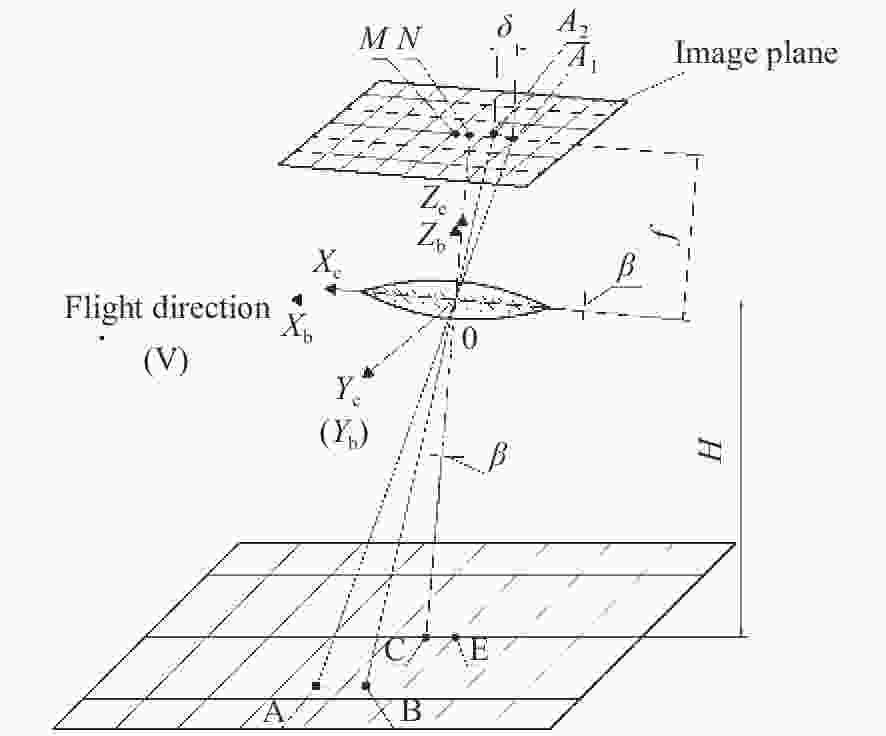
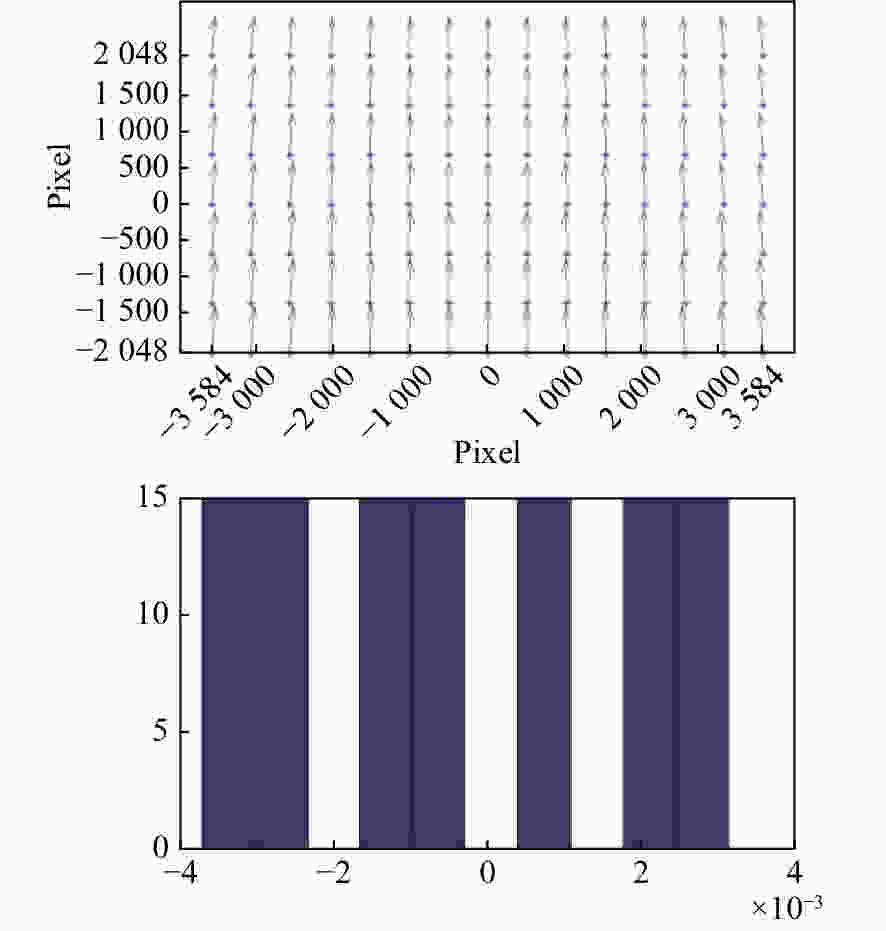
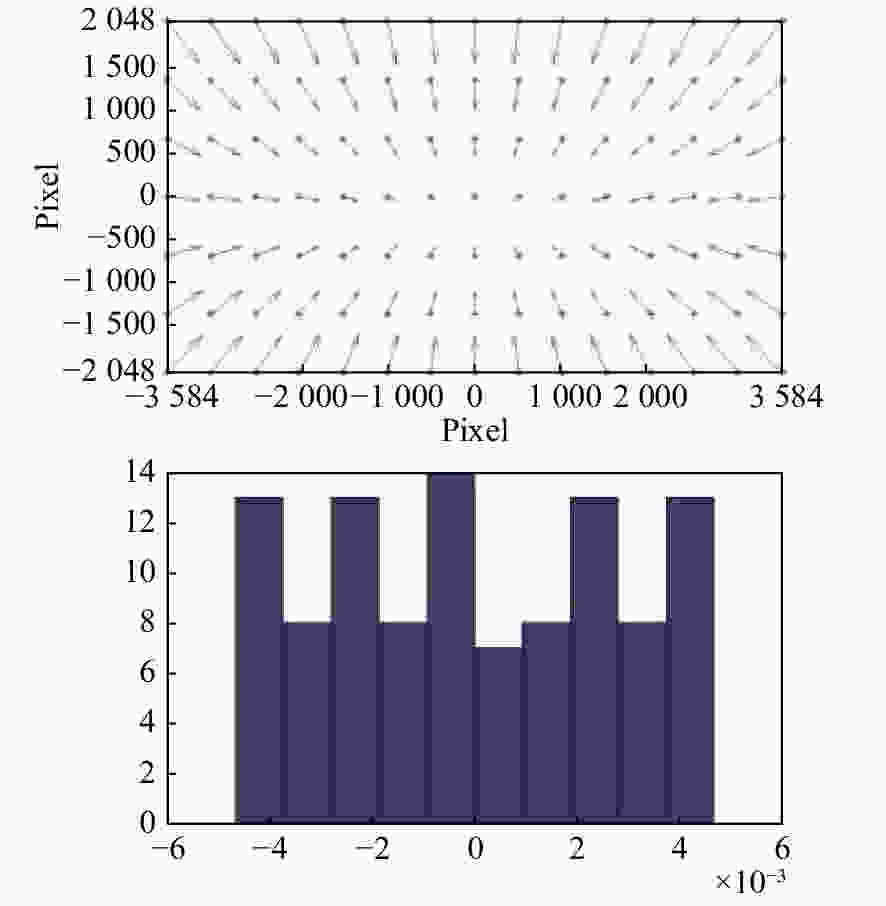
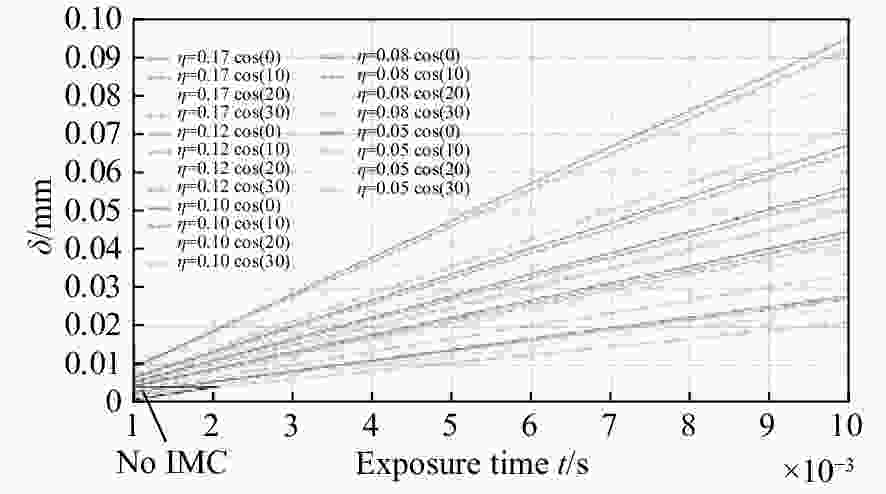
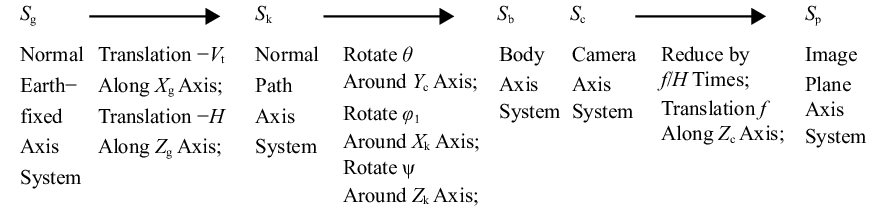
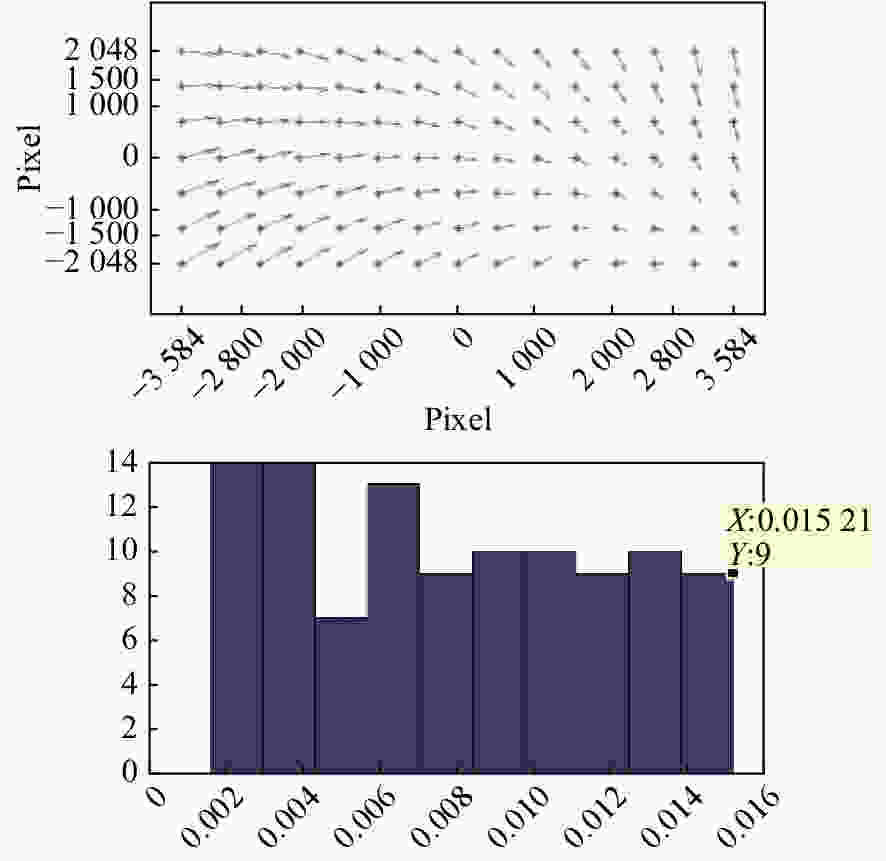
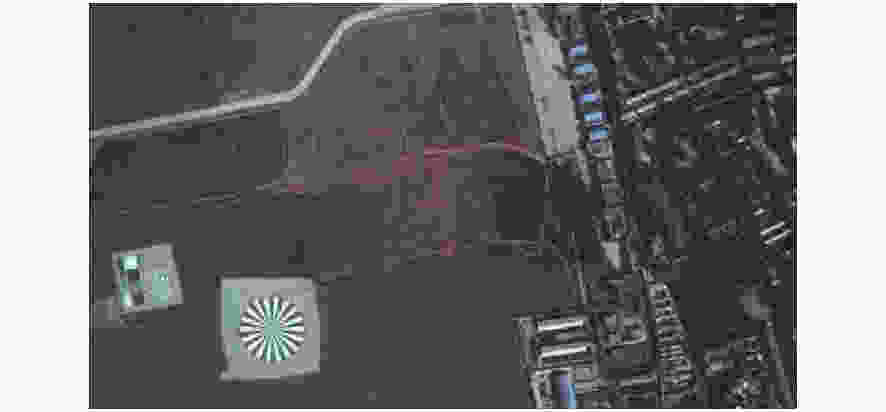
摘要: 为了提高航空遥感相机的摄影分辨率，获得高分辨率的航空图像，除了采用具有高传递函数的光学系统和高质量成像介质外，还要正确控制快门的曝光时间，以保证探测器能够获得合适的像移量。本文基于一种航空测绘相机镜间快门的结构形式及工作原理，以笛卡尔理论为基础，通过坐标变换方法，建立地面目标和影像之间的矩阵关系，从而确定快门曝光时间和像移量的关系，接着，结合相机速高比、像元尺寸等参数，对像移量及像移残差进行分析。根据相机的不同安装方式，以像移残差为1/3像元尺寸为标准，判定成像系统是否加入像移补偿机构，为相机设计提供理论依据。通过静态测试及飞行试验对分析进行验证。试验结果表明，相机分辨力达到36.8 lp/mm，航拍图像良好，满足指标要求。
- 镜间快门 /
- 像移量 /
- 曝光时间 /
- 像移残差 /
- 像移补偿
Abstract: In order to improve the photographic resolution of aerial remote sensing cameras and obtain high-resolution aerial images, besides optical system with high modulation transfer function and high-quality imaging medium, the exposure time of shutter should be controlled correctly to ensure that the detector can obtain an appropriate image motion value. Based on the structure and working principle of the lens shutter of an aerial mapping camera, we establish the matrix relationship between the ground object and the image through coordinate transformation method, that is, the relationship between the exposure time of the shutter and the image motion value is determined. The image motion value and residual error of the image motion are analyzed by combining the parameters of the camera speed-height ratio and the pixel size. According to the different installation modes of the aerial camera, when the residual error of the image motion value is more than 1/3 of a pixel in size, the Image Motion Compensation (IMC) mechanism is necessary to the imaging system. Thus a theoretical basis for the design of the IMC mechanism in an aerial camera is provided. The analysis is validated by a static test and flight test. The test results show that the aerial camera clearly captures images and the spatial resolution of its images reaches 36.8 lp/mm, which meets the requirements of our technical index.
- lens shutter /
- image motion /
- exposure time /
- residual error of image motion /
- Image Motion Compensation (IMC)

HTML全文

Figure 1. Photograph of shutter

下载: 全尺寸图片幻灯片

Figure 2. Schematic diagram of blade scanning aperture

下载: 全尺寸图片幻灯片

Figure 3. Forward image shift in camera mounted vertically

下载: 全尺寸图片幻灯片

Figure 4. Image motion vector in camera mounted vertically

下载: 全尺寸图片幻灯片

Figure 5. The relationship between exposure time and image motion value at difference speed-height ratios

下载: 全尺寸图片幻灯片

Figure 6. Image motion in camera mounted tilting forward

下载: 全尺寸图片幻灯片

Figure 7. Schematic and histogram of image motion vector in camera lean mounted forward

下载: 全尺寸图片幻灯片

Figure 8. Schematic and histogram of forward residual image motion in camera mounted leaning forward

下载: 全尺寸图片幻灯片

Figure 9. The relationship between exposure time and image shift at difference V/H and lean angle forward

下载: 全尺寸图片幻灯片

Figure 10. Diagram of coordinate transformation relation

下载: 全尺寸图片幻灯片

Figure 11. The schematic and histogram of image shift vectors caused by aircraft attitude changes

下载: 全尺寸图片幻灯片

Figure 12. Schematic diagram of experimental device

下载: 全尺寸图片幻灯片

Figure 13. Measuring setup

下载: 全尺寸图片幻灯片

Figure 14. Photo of the dynamic target

下载: 全尺寸图片幻灯片

Figure 15. Radial drone image in flight

下载: 全尺寸图片幻灯片

Table 1. Imaging experiment results

Measurement times Visual resolution(lp/mm)

1 36.5
2 36.5
3 37.2
4 36.5
5 37.2
Average 36.8

下载: 导出CSV

参考文献(13)

[1]	SIERBAKOV. Design and Calculation of Aerial Camera[M]. SUN ZH ZH, ZHOU G Q, trans. Jilin: The Association of Science and Technology Translation in Jilin, 1985. (in Chinese)
[2]	WANG ZH ZH. Photogram Metry Principle[M]. Beijing: Surveying and Mapping Press, 1979. (in Chinese)
[3]	ZHANG L, DING Y L, ZHANG H W, et al. Design and precision analysis of curtain type shutter based on timing belt[J]. Optics and Precision Engineering, 2013, 21(2): 380-387. (in Chinese) doi: 10.3788/OPE.20132102.0380
[4]	DURFEE D, JOHNSON W, MCLEOD S. Advanced electro-mechanical micro-shutters for thermal infrared night vision imaging and targeting systems[J]. Proceedings of SPIE, 2007, 6452: 65422C.
[5]	LIU M, LIU G, LI Y Y, et al. The effect of image motion on the quality of aerial camera images[J]. Opto-Electronic Engineering, 2004, 31(S1): 12-14. (in Chinese)
[6]	YUAN G Q. Research on the calibration of inner orientation elements for area scan color CCD mapping camera with forward image motion compensation mechanism[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2012. (in Chinese)
[7]	YU CH F, LI H, JIA P, et al. Lens shutter for aerial photography[J]. Optics and Precision Engineering, 2018, 26(1): 105-113. (in Chinese) doi: 10.3788/OPE.20182601.0105
[8]	REN H, YUAN H Y. Research on image motion compensation of airborne camera of focal plane CCD[J]. Semiconductor Optoelectronics, 2011, 32(3): 417-420, 428. (in Chinese)
[9]	YU CH F. Design and analysis of optical characteristic on new type aerial lens shutter[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2013. (in Chinese)
[10]	YAN CH X, WANG J Q. Method of coordinate transformation for IM&IMC calculation in aerospace camera system[J]. Optics and Precision Engineering, 2000, 8(3): 203-207. (in Chinese)
[11]	CHEN B Y. Local linear enhancement of luminance histogram of color remote sensing image[J]. Optics and Precision Engineering, 2017, 25(2): 502-508. (in Chinese) doi: 10.3788/OPE.20172502.0502
[12]	WANG J Q, YU P, YAN CH X, et al. Space optical remote sensor image motion velocity vector computational modeling[J]. Acta Optica Sinica, 2004, 24(12): 1585-1589. (in Chinese) doi: 10.3321/j.issn:0253-2239.2004.12.001
[13]	LI G, YANG M Y. Image motion measurement for airborne camera based on joint transform correlation[J]. Chinese Journal of Optics, 2015, 8(3): 401-406. (in Chinese) doi: 10.3788/co.20150803.0401