长周期光纤光栅光谱特性仿真研究

朱雨雨; 郗亚茹; 张亚妮; 江鹏; 薛璐; 许强

doi:10.3788/CO.2019-0152

长周期光纤光栅光谱特性仿真研究

doi: 10.3788/CO.2019-0152

cstr: 32171.14.CO.2019-0152

朱雨雨^{1, 3,},
郗亚茹^{1, 3},
张亚妮^{1, 2, 3, ,},
江鹏^{1, 3},
薛璐^{1, 3},
许强^{1, 3,}

1.
宝鸡文理学院物理与光电技术学院，宝鸡 721016
2.
陕西科技大学文理学院，西安 710021
3.
宝鸡市超快激光与新材料工程技术研究中心，宝鸡 721016

基金项目: 国家自然科学基金(No. 11647008)；陕西省国际科技合作与交流项目（No. 2018KW-016）；瞬态光学与光子技术国家重点实验室开放基金（No. SKLST201802）；宝鸡市重大科技专项计划项目（No. 2015CXNL-1-3）；咸阳市科技计划项目（No. 2018K02-60）；陕西科技大学重点科研项目资助（No. 2018WLXY-01-01）

详细信息

作者简介:
朱雨雨（1994−)，女，陕西渭南人，硕士研究生，2017年至今就读于宝鸡文理学院光学工程专业，主要研究方向为光纤光栅与传感。E-mail：121747851@qq.com

张亚妮（1966−），女，陕西宝鸡人，教授，博士，硕士生导师。主要研究方向为微纳光子学器件、光纤光栅传感与光纤激光器。E-mail：yanizhang1@163.com

中图分类号: TN249
计量
- 文章访问数: 3599
- HTML全文浏览量: 3133
- PDF下载量: 375
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-15
- 修回日期: 2019-08-30
- 刊出日期: 2020-06-01

Numerical simulation of transmission spectra characterization of long-period fiber grating

ZHU Yu-yu^{1, 3
,},
XI Ya-ru^{1, 3},
ZHANG Ya-ni^{1, 2, 3
, ,},
JIANG Peng^{1, 3},
XUE Lu^{1, 3},
XU Qiang^{1, 3
,}

1.
School of Physics and Optoelectronics Technology, Baoji University of Arts & Science, Baoji 721016, China
2.
School of Arts and Sciences, Shaanxi University of Science & Technology, Xi’an 710021, China
3.
Baoji Engineering Technology Research Center on Ultrafast Laser and New Materials, Baoji 721016, China

Funds: Supported by National Natural Science Foundation of China (No. 11647008); International Science & Technology Cooperation and Exchanges Project of Shaanxi (No. 2018KW-16); Open Research Fund of State Key Laboratory of Transient Optics and Photonics (No. SKLST201802); Key Sciences and Technology Project of Baoji City (No. 2015CXNL-1-3); Science and Technology Project of Xianyang City (No. 2018K02-60); Key Research Project of Shaanxi University of Science & Technology (No. 2018WLXY-01-01)

More Information

Corresponding author: yanizhang1@163.com;; xuqiang@snnu.edu.cn

摘要

摘要: 基于耦合模理论，利用传输矩阵法求解出长周期光纤光栅(Long Period Fiber Gratings，LPFGs)的透射谱表达式，模拟分析了LPFGs的光谱特性与光栅参数如周期、刻写长度以及折射率调制深度之间的关系。研究结果表明：LPFGs谐振波长随着周期和折射率调制深度的增大向长波方向移动，且高次模谐振波长对光栅周期更为敏感；光谱带宽的变化主要取决于光栅的刻写长度，随着光栅刻写长度的增加，带宽逐渐变窄，且当光栅刻写长度大于5.2 cm时，光栅存在过耦合区域；随着折射率调制深度的增加，光栅存在不完全耦合、完全耦合和过耦合现象，且谐振损耗最大值位置随着折射率调制深度的增加逐渐向低次转移。该研究结论对长周期光纤光栅的理论分析和实际应用中的参数设计具有重要参考价值。
- 长周期光纤光栅 /
- 耦合模理论 /
- 透射谱
Abstract: Based on the coupled-mode theory, the equation for the transmission spectrum of Long Period Fiber Gratings (LPFGs) is solved by using the transmission matrix method and the relationship between the spectral characteristics of LPFGs and grating parameters (such as grating period, writing length and the depth of refractive index modulation) is simulated. The results show that the resonant wavelength of LPFGs is red-shifted with an increase in the grating period and refractive index modulation depth, and that the resonant wavelength with higher-order mode is relatively more sensitive on the grating period. At the same time, the change in the spectral bandwidth mainly depends on the writing length of the grating. The bandwidth narrows gradually with an increase in the length of the grating and over-coupling occurs when the grating length is higher than 5.2 cm. With an increase in the refractive index modulation depth, the grating has the phenomena of incomplete coupling, complete coupling and over-coupling, and the position of the maximum resonance loss will gradually transfer to the lower-order mode. The results of this research have important referential significance for the theoretical research of LPFGs and parameter designs in practical applications.
- long period fiber grating /
- the coupled-mode theory /
- transmission spectrum

HTML全文

图 1 阶跃折射率光纤三层模型截面图

Figure 1. Cross section of three-layer structure for the step refractive index fiber

下载: 全尺寸图片幻灯片

图 2 (a) LPFGs透射谱随光栅周期变化曲线；(b)谐振波长随光栅周期的变化曲线

Figure 2. (a) Transmission spectrum of LPFGs at different periods; (b) relationship between resonance wavelength and grating period

下载: 全尺寸图片幻灯片

图 3 LPFGs透射谱损耗随光栅刻写长度变化曲线。(a) LPFGs透射谱；(b)谐振峰损耗随光栅刻写长度变化

Figure 3. Transmission loss of LPFGs at different grating lengths. (a) Transmission spectra of LPFGs; (b) relationship between resonance loss and grating length

下载: 全尺寸图片幻灯片

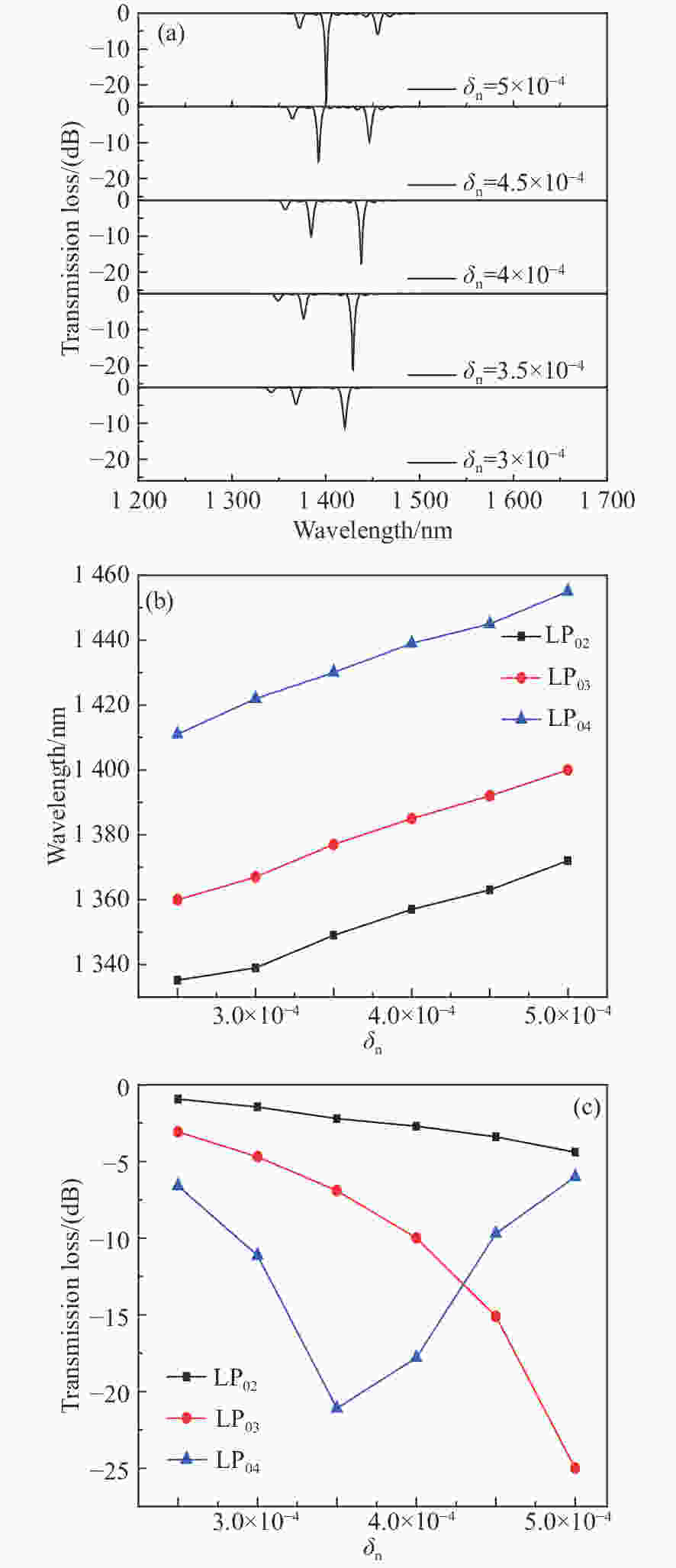
图 4 LPFGs透射谱随折射率调制深度δ_n的变化曲线。 (a) LPFGs透射谱；(b)谐振波长和(c)谐振峰损耗值随折射率调制深度δ_n的变化

Figure 4. Transmission spectra of LPFGs at different depthes of refractive index modulation. (a) Transmission spectra of LPFGs; relation of the resonance wavelength (b) and transmission loss (c) with depth of refractive index modulation.

下载: 全尺寸图片幻灯片

参考文献(24)

[1]	ERDOGAN T. Cladding-mode resonances in short- and long-period fiber grating filters: errata[J]. Journal of the Optical Society of America A, 2000, 14(18): 1760-1773. doi: 10.1364/JOSAA.17.002113
[2]	石胜辉, 赵明富, 罗彬彬, 等. 扭转螺旋型力学微弯长周期光纤光栅的光谱特性[J]. 光学精密工程,2017,25(7):1771-1776. SHI SH H, ZHAO M F, LUO B B, et al. Spectral characteristics of helicoidal mechanically-induced long-period fiber grating[J]. Optics and Precision Engineering, 2017, 25(7): 1771-1776. (in Chinese)
[3]	杨颖, 顾铮. 长周期光纤光栅透射谱计算方法的比较与分析[J]. 光子学报,2012,41(7):824-830. doi: 10.3788/gzxb20124107.824 YANG Y, GU ZH. Comparing and analysis of calculation methods of long-period fiber gratings transmission spectra[J]. Acta Photonica Sinica, 2012, 41(7): 824-830. (in Chinese) doi: 10.3788/gzxb20124107.824
[4]	赵明富, 韩汐, 罗彬彬, 等. 长周期光纤光栅的折射率梯度响应特性[J]. 光学精密工程,2013,21(2):316-322. doi: 10.3788/OPE.20132102.0316 ZHAO M F, HAN X, LUO B B, et al. Response characteristics of refractive-index gradient based on long-period fiber gratings[J]. Optics and Precision Engineering, 2013, 21(2): 316-322. (in Chinese) doi: 10.3788/OPE.20132102.0316
[5]	曾祥楷, 饶云江. 长周期光纤光栅傅里叶模式耦合理论[J]. 物理学报,2010,59(12):8607-8614. doi: 10.7498/aps.59.8607 ZENG X K, RAO Y J. Theory of Fourier mode coupling for long-period fiber gratings[J]. Acta Physica Sinica, 2010, 59(12): 8607-8614. (in Chinese) doi: 10.7498/aps.59.8607
[6]	徐新华, 崔一平. 矩形折射率调制型长周期光纤光栅传输谱的理论分析及数值计算[J]. 物理学报,2003,52(1):96-101. doi: 10.3321/j.issn:1000-3290.2003.01.019 XU X H, CUI Y P. Theoretical analysis and numerical calculation for the transmission spectrum of long-period fiber gratings with a rectangular index modulation[J]. Acta Physica Sinica, 2003, 52(1): 96-101. (in Chinese) doi: 10.3321/j.issn:1000-3290.2003.01.019
[7]	吴清海, 秦子雄, 曾庆科, 等. 长周期光纤光栅透射谱仿真的新方法[J]. 广西通信技术,2007(2):23-26, 35. doi: 10.3969/j.issn.1008-3545.2007.02.006 WU Q H, QIN Z X, ZENG Q K, et al. A new method of simulation research on the transmission spectrum of long-period fiber grating[J]. Guangxi Communication Technology, 2007(2): 23-26, 35. (in Chinese) doi: 10.3969/j.issn.1008-3545.2007.02.006
[8]	高敏, 葛海波, 李盼盼, 等. 不同长周期光栅的级联传输谱特性[J]. 光通信技术,2018,42(11):56-59. GAO M, GE H B, LI P P, et al. Cascaded transmission spectrum characteristics of different long-period fiber grating[J]. Optical Communication Technology, 2018, 42(11): 56-59. (in Chinese)
[9]	YANG M W, WANG D N, WANG Y, et al. Long period fiber grating formed by periodically structured microholes in all-solid photonic bandgap fiber[J]. Optics Express, 2010, 18(3): 2183-2189. doi: 10.1364/OE.18.002183
[10]	MIZRAHI V, SIPE J E. Optical properties of photosensitive fiber phase gratings[J]. Journal of Lightwave Technology, 1993, 11(10): 1513-1517. doi: 10.1109/50.249888
[11]	TAGHIPOUR A, ROSTAMI A, BAHRAMI M, et al. Comparative study between LPFG- and FBG-based bending sensors[J]. Optics Communications, 2014, 312(4): 99-105. doi: 10.1016/j.optcom.2013.09.020
[12]	李新碗, 杜鹏超, 叶爱伦. 长周期光纤光栅耦合特性及模拟分析[J]. 电子学报,2000,28(11):68-71. doi: 10.3321/j.issn:0372-2112.2000.11.018 LI X W, DU P CH, YE A L. The analysis and simulation on the mode-coupling characteristics of long-period fiber grating[J]. Acta Electronica Sinica, 2000, 28(11): 68-71. (in Chinese) doi: 10.3321/j.issn:0372-2112.2000.11.018
[13]	CHUNG K W, YIN SH ZH. Analysis of a widely tunable long-period grating by use of an ultrathin cladding layer and higher-order cladding mode coupling[J]. Optics Letters, 2004, 29(8): 812-814. doi: 10.1364/OL.29.000812
[14]	WANG H Y, CHUO S M, WANG L A. Fabrication and simulation of corrugated long period microfiber gratings[J]. Proceedings of SPIE, 2011, 7753(4): 123-130. doi: 10.1117/12.886086
[15]	ERDOGAN T. Fiber grating spectra[J]. Journal of Lightwave Technology, 1997, 15(8): 1277-1294. doi: 10.1109/50.618322
[16]	何万迅, 施文康. 模式耦合理论在圆周对称长周期光纤光栅建模中的应用[J]. 光学技术,2002,28(2):155-157. doi: 10.3321/j.issn:1002-1582.2002.02.039 HE W X, SHI W K. Application of coupled mode theory on modeling for circularly symmetric LPFG[J]. Optical Technique, 2002, 28(2): 155-157. (in Chinese) doi: 10.3321/j.issn:1002-1582.2002.02.039
[17]	MCCALL M. On the application of coupled mode theory for modeling fiber bragg gratings[J]. Journal of Lightwave Technology, 2000, 18(2): 236-242. doi: 10.1109/50.822798
[18]	欧启标, 覃溪, 张超, 等. 长周期光纤光栅折射率特性仿真的新方法[J]. 光学技术,2012,38(1):60-63. doi: 10.3788/GXJS20123801.0060 OU Q B, QIN X, ZHANG CH, et al. A new method of simulation of LPFG refractive index characteristics[J]. Optical Technique, 2012, 38(1): 60-63. (in Chinese) doi: 10.3788/GXJS20123801.0060
[19]	张亚妮, 刘思聪, 赵亚, 等. 800 nm高能量飞秒激光脉冲刻写长周期光纤光栅机理[J]. 光子学报,2018,47(1):0106003. doi: 10.3788/gzxb20184701.0106003 ZHANG Y N, LIU S C, ZHAO Y, et al. Fabrication mechanism of long-period fiber grating based on 800 nm high intensity femto-second laser pulses[J]. Acta Photonica Sinica, 2018, 47(1): 0106003. (in Chinese) doi: 10.3788/gzxb20184701.0106003
[20]	张亚妮, 郗亚茹, 江鹏, 等. 飞秒激光直写长周期光纤光栅及其光谱特性[J]. 光子学报,2018,47(11):1106001. doi: 10.3788/gzxb20184711.1106001 ZHANG Y N, XI Y R, JIANG P, et al. Fabrication of long period fibre gratings by femtosecond laser writing directly and its spectral characteristics[J]. Acta Photonica Sinica, 2018, 47(11): 1106001. (in Chinese) doi: 10.3788/gzxb20184711.1106001
[21]	ZHANG Y N, XI Y R, LIU S C, et al. Long-period fiber grating fabricated by 800 nm femtosecond laser pulses[J]. Proceedings of SPIE, 2018, 10697: 106974Q.
[22]	赵鹏, 刘云, 洪欢欢, 等. 纳米金辅助介质阻挡放电离子化质谱分析法在兽药饲料快检中的应用[J]. 分析化学,2018,46(7):1089-1094. ZHAO P, LIU Y, HONG H H, et al. Fast analysis of veterinary drugs in feed using gold nanoparticles-assisted dielectric barrier discharge ion source-mass spectrometry[J]. Chinese Journal of Analytical Chemistry, 2018, 46(7): 1089-1094. (in Chinese)
[23]	余登斌, 江岚, 王沛,等. 碳纳米材料修饰阳极电极对微生物燃料电池传感器水体毒性检测灵敏度的影响[J]. 分析化学,2018,46(7):1032-1038. YU D B, JIANG L, WANG P, et al. Effect of anode electrode modified with carbon nanomaterials of microbial fuel cell-based sensor on detection sensitivity of water toxicity[J]. Chinese Journal of Analytical Chemistry, 2018, 46(7): 1032-1038. (in Chinese)
[24]	贾玮, 张荣, 石琳,等. 基于质谱断裂机理的乳制品中农药非定向筛查分析方法构建[J]. 分析化学,2019,47(7):1098-1105. JIA W, ZHANG R, SHI L, et al. Construction of non-target screening method for pesticides in milk and dairy products based on mass spectrometry fracture mechanism[J]. Chinese Journal of Analytical Chemistry, 2019, 47(7): 1098-1105. (in Chinese)