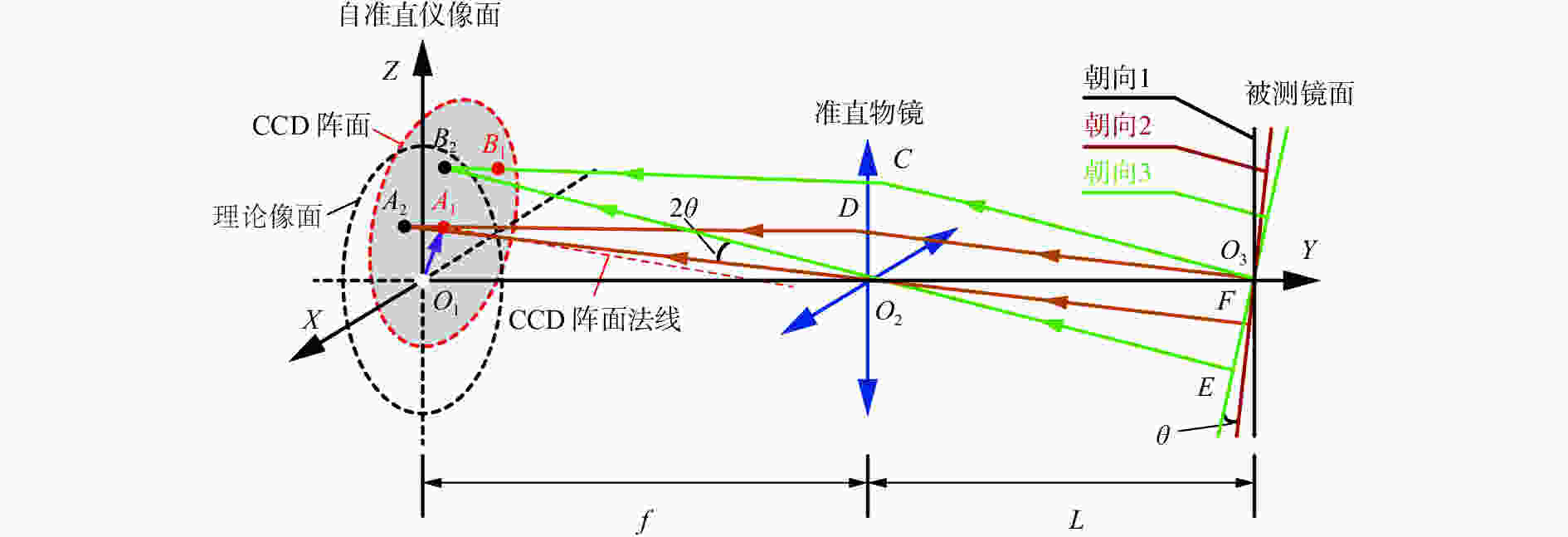
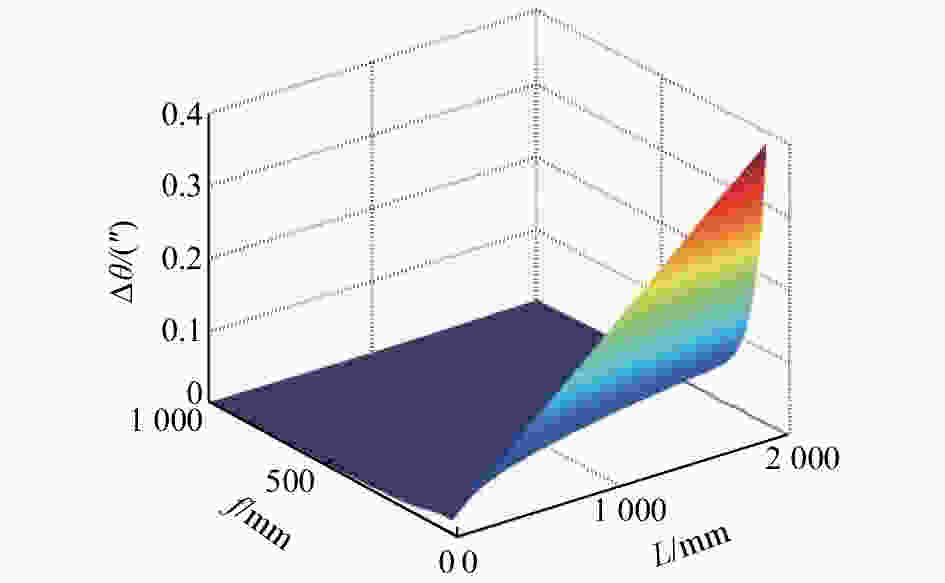
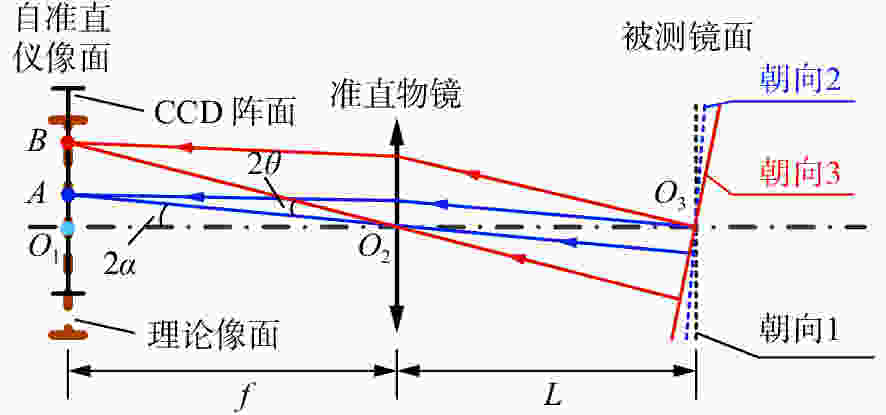
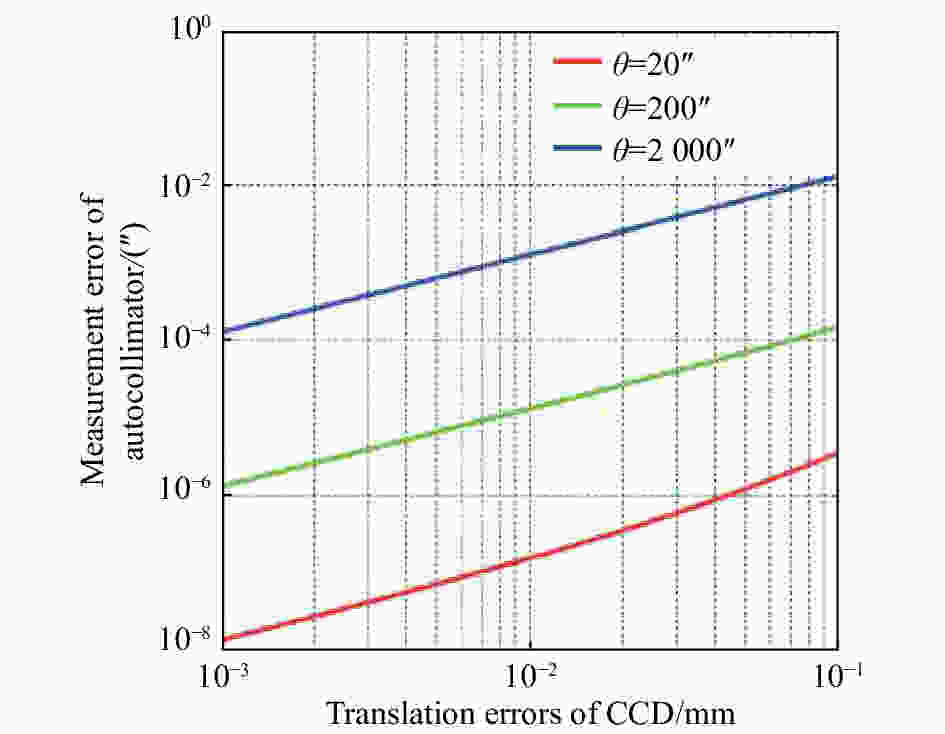
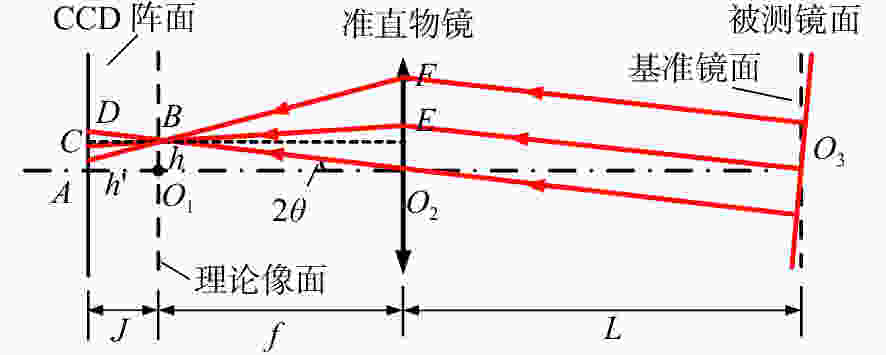
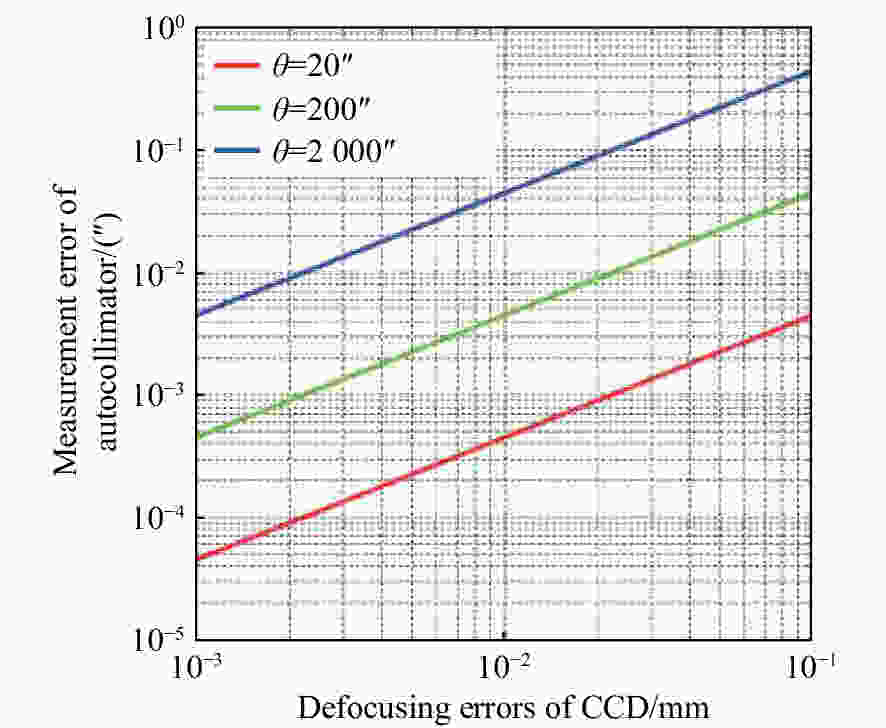
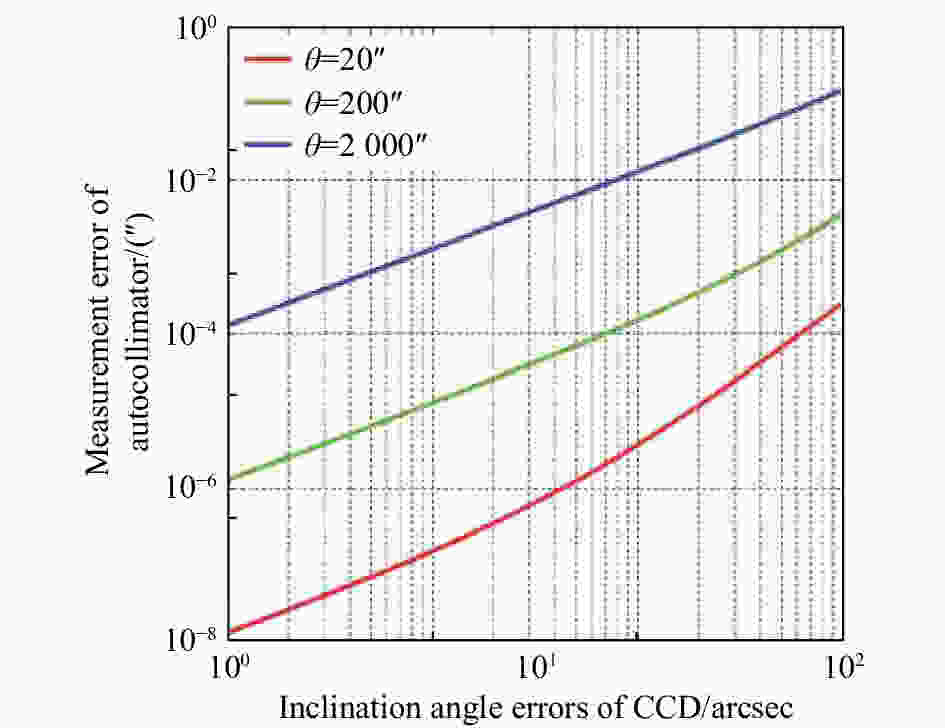
-
摘要: 本文首次提出并构建了自准直仪光电探测器失调的数学模型。基于该模型，分析了光电探测器相对于理论像面处于空间任意位置和朝向时对自准直仪测角的影响。结果表明，探测器失调造成的测角误差随准直物镜焦距f的增大而减小，随自准直仪到被测镜面的距离L以及待测角度θ的增大而增大。计算发现，当f=300 mm，L=100 mm，θ=20″时，因探测器失调引起的测角误差达到0.004 5″。文章进一步分析了各种探测器失调误差单独作用时对自准直仪测角的影响，验证了模型的正确性，并发现探测器离焦对自准直仪的影响最大。根据本文计算结果，选择长焦距的成像物镜、减小测量距离、提高光电探测器沿轴向的安装精度是减小光电探测器失调对自准直仪影响的关键。基于提出的数学模型，可以系统地计算探测器失调对自准直仪测角的影响，进而为构建更加完善的自准直仪误差模型奠定基础。Abstract: As one of the key errors in autocollimators, misalignment of the photodetector is analyzed and modeled carefully in this paper. Effect of misalignment of the photodetector on angle measurements is characterized, when the photodetector in any position and orientation in space with respect to the theoretical image plane of autocollimators. It is shown that the angular measurement errors of autocollimators induced by a misaligned photodetector increase with greater measuring range L, larger angle θ and smaller focal length f of the collimating object lens. When f=300 mm, L=100 mm, θ=20″, the angular measurement error caused by a misaligned photodetector is 0.004 5″. The effects of each photodetector misalignment error on angle measurements in autocollimators are characterized. The model proposed in this paper is validated. Among all kinds of photodetector misalignment errors, the defocusing error has the greatest influences on autocollimators. Hence, it is critical to choose an imaging objective with longer focal length, reduce the measurement distance, and improve the installation accuracy of the photodetector along the axis. The model proposed in this paper helps to systematically obtain the angular measurement errors caused by a misaligned photodetector, which will play a key role in building a better error analysis model for autocollimators.
-
Key words:
- autocollimator /
- angular measurement accuracy /
- misaligned photodetector /
- error analysis
-
图 2 CCD阵面失调的自准直仪光路
Figure 2. Optical path of autocollimator with a misaligned CCD array
图 3 自准直仪CCD阵面失调建模流程图
Figure 3. Flowchart of CCD misalignment modeling of autocollimator
图 4 自准直仪CCD阵面失调导致的测角误差
Figure 4. Angular measurement errors of autocollimators with a misaligned CCD
图 5 CCD失调参数一定时，自准直仪测角误差随焦距f和测量距离L的变化关系
Figure 5. The relationship between measurement errors of autocollimators and focal length f, and measuring length L when CCD misalignment parameters are constant
图 7 自准直仪测角误差随CCD阵面平移误差的变化曲线
Figure 7. Angular measurement errors in autocollimator varying with translation error of CCD
图 9 自准直仪测角误差随CCD阵面离焦误差的变化曲线
Figure 9. Angular measurement errors of autocollimators varying with defocusing errors of CCD
图 10 自准直仪CCD阵面出现倾斜误差
Figure 10. Inclination angle errors occuring in CCD of autocollimator
图 11 自准直仪测角误差随CCD阵面倾斜误差的变化曲线
Figure 11. Angular measurement errors in autocollimator varying with inclination angle error of CCD
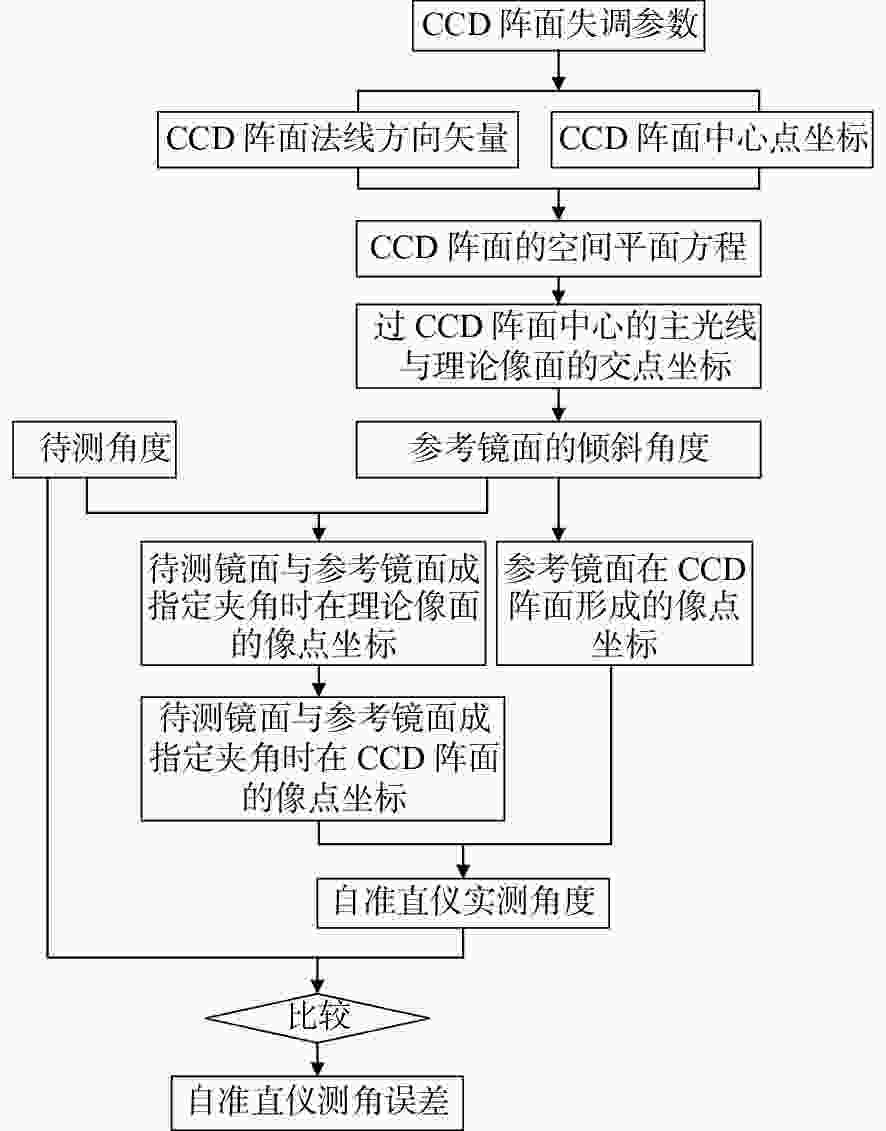
表 1 CCD阵面失调参数
Table 1. Misalignment parameters of CCD
失调参数 最小值 最大值 取样数 a/mm −0.1 0.1 11 b/mm −0.1 0.1 11 c/mm −0.1 0.1 11 $\alpha $/(″) −360 360 11 $\beta $/(″) −360 360 11 $\gamma $/(″) −360 360 11 
下载: 导出CSV
表 2 CCD阵面失调导致的测角误差
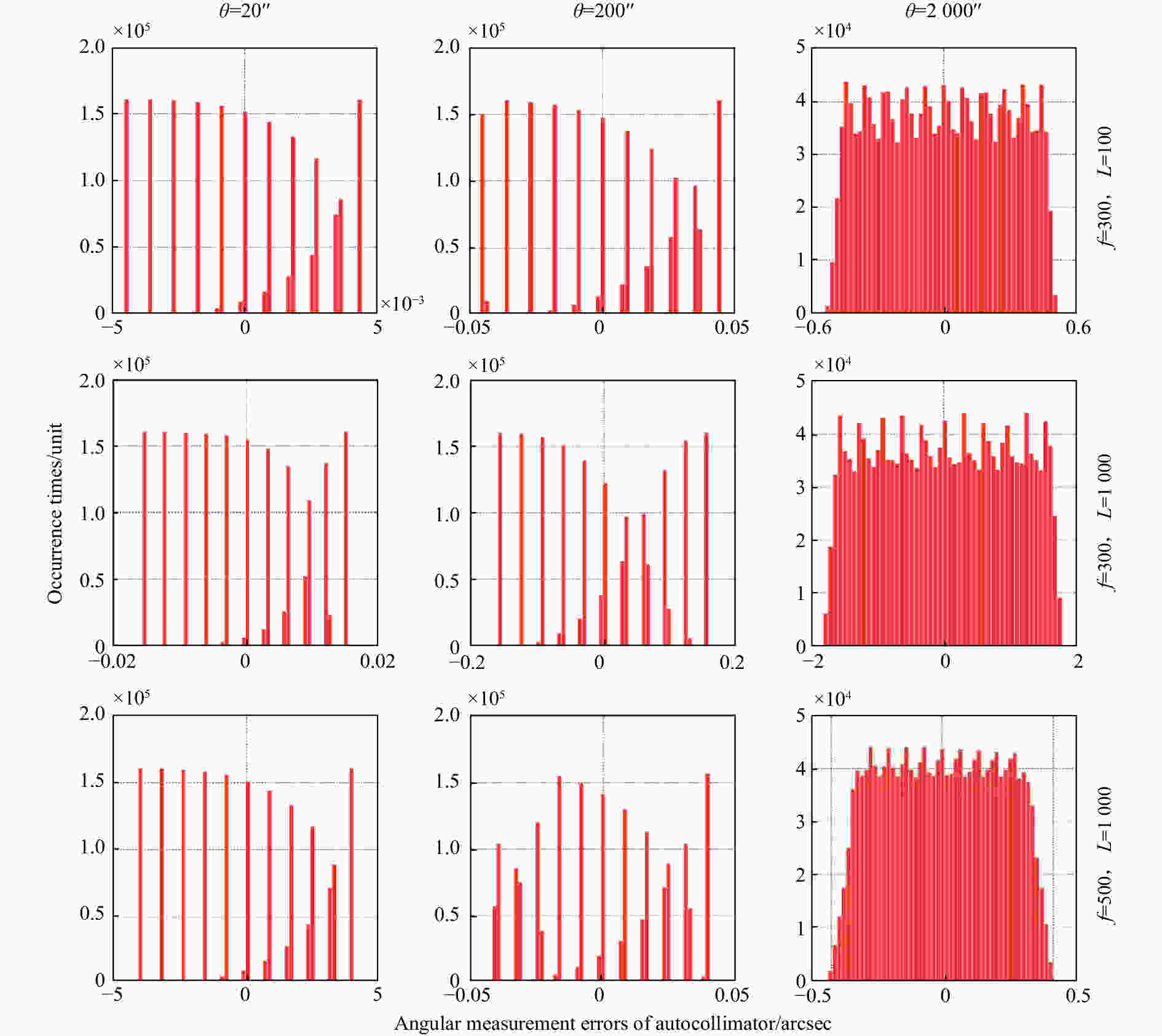
Table 2. Angular measurement errors induced by a misaligned CCD
f, L/mm $\theta $/(″) 20 200 2 000 f=300, L=100 0.004 5 0.046 0.53 f=300, L=1 000 0.016 0.16 1.8 f=500, L=1 000 0.004 1 0.042 0.51
下载: 导出CSV
-
[1] 朱凡. 基于共光路光束漂移测量与同步补偿的激光自准直技术[D]. 哈尔滨: 哈尔滨工业大学, 2013.ZHU F. Laser autocollimation technology based on common-path beam drift measurement and synchronous compensation[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese) [2] 黄银国. 激光自准直微小角度测量基础技术研究[D]. 天津: 天津大学, 2010.HUANG Y G. Study on micro-angle measuring basic technique of laser autocollimation[D]. Tianjin: Tianjin University, 2010. (in Chinese) [3] 田留德, 赵建科, 王涛, 等. 测试设备位姿失调对自准直仪法测量圆分度误差的影响[J]. 光学 精密工程,2017,25(9):2267-2276. doi: 10.3788/OPE.20172509.2267TIAN L D, ZHAO J K, WANG T, et al. Influence of test equipment pose error on dividing error measurement based on autocollimator[J]. Optics and Precision Engineering, 2017, 25(9): 2267-2276. (in Chinese) doi: 10.3788/OPE.20172509.2267 [4] 杨飞, 安其昌, 张静, 等. 大口径光学系统的镜面视宁度检测[J]. 光学 精密工程,2017,25(10):2572-2579. doi: 10.3788/OPE.20172510.2572YANG F, AN Q CH, ZHANG J, et al. Seeing metrology of large aperture mirror of telescope[J]. Optics and Precision Engineering, 2017, 25(10): 2572-2579. (in Chinese) doi: 10.3788/OPE.20172510.2572 [5] 王国名, 劳达宝, 周维虎. 光电自准直经纬仪光学系统设计与公差分析[J]. 激光与光电子学进展,2017,54(10):102203.WANG G M, LAO D B, ZHOU W H. Optical system design and tolerance analysis of photoelectric self-collimation theodolite[J]. Laser &Optoelectronics Progress, 2017, 54(10): 102203. (in Chinese) [6] 闫钰锋, 吴震, 王洋, 等. 温度变化对自准直仪机械结构的影响[J]. 光学仪器,2017,39(1):41-45.YAN Y F, WU ZH, WANG Y, et al. Effect of temperature on mechanical structure of autocollimator[J]. Optical Instruments, 2017, 39(1): 41-45. (in Chinese) [7] 楼志斌, 赵辉, 刘权, 等. 结合激光准直的二维转角动态测量系统[J]. 光学 精密工程,2019,27(3):561-568. doi: 10.3788/OPE.20192703.0561LOU ZH B, ZHAO H, LIU Q, et al. Two-dimensional rotation angle dynamic measurement system combining laser collimation[J]. Optics and Precision Engineering, 2019, 27(3): 561-568. (in Chinese) doi: 10.3788/OPE.20192703.0561 [8] 何煦, 杨雪, 李颐, 等. 大口径空间光学望远镜重力卸载点布局优化方法[J]. 光学 精密工程,2018,26(11):2764-2775. doi: 10.3788/OPE.20182611.2764HE X, YANG X, LI Y, et al. Gravity compensation optimization algorithm for large aperture spatial optical telescope[J]. Optics and Precision Engineering, 2018, 26(11): 2764-2775. (in Chinese) doi: 10.3788/OPE.20182611.2764 [9] JUST A, KRAUSE M, PROBST R, et al. Calibration of high-resolution electronic autocollimators against an angle comparator[J]. Metrologia, 2003, 40(5): 288-294. doi: 10.1088/0026-1394/40/5/011 [10] GECKELER R D, JUST A. Optimized use and calibration of autocollimators in deflectometry[J]. Proceedings of SPIE, 2007, 6704: 670407. doi: 10.1117/12.732384 [11] 陈颖, 张学典, 逯兴莲, 等. 自准直仪的现状与发展趋势[J]. 光机电信息,2011,28(1):6-9. doi: 10.3788/OMEI20112801.0006CHEN Y, ZHANG X D, LU X L, et al. Current situation and development trend of autocollimator[J]. OME Information, 2011, 28(1): 6-9. (in Chinese) doi: 10.3788/OMEI20112801.0006 [12] 赵玉平, 彭川黔, 王劼. 大口径细光束自准直测量系统的误差源分析[J]. 半导体光电,2018,39(3):414-419.ZHAO Y P, PENG CH Q, WANG J. Analysis of error source for large aperture thin beam auto-collimating measurement system[J]. Semiconductor Optoelectronics, 2018, 39(3): 414-419. (in Chinese) [13] 欧同庚, 陈志高, 杨博雄, 等. CCD光电自准直仪工作原理及误差源分析[J]. 大地测量与地球动力学,2007,27(S1):98-100.OU T G, CHEN ZH G, YANG B X, et al. Operating principle and error source of a new type of CCD photoelectric autocollimator[J]. Journal of Geodesy and Geodynamics, 2007, 27(S1): 98-100. (in Chinese) [14] 张冬, 王振宏. PSD光电自准直仪工作原理及误差分析[J]. 机械工程师,2014(12):46-47. doi: 10.3969/j.issn.1002-2333.2014.12.019ZHANG D, WANG ZH H. Operation principle and error analysis of PSD photoelectric autocollimator[J]. Mechanical Engineer, 2014(12): 46-47. (in Chinese) doi: 10.3969/j.issn.1002-2333.2014.12.019 -
下载:
计量
- 文章访问数: 2754
- HTML全文浏览量: 1028
- PDF下载量: 118
- 被引次数: 0
