Error analysis and fabrication of low-stepped mirrors
doi: 10.3788/CO.20191204.0791
-
摘要: 本文提出了一种基于多级微反射镜和栅格分束器的静态轻型傅立叶红外变换光谱仪，通过两个多级微反射镜实现光程差的空间离散和干涉图的静态二维采样，通过引入栅格分束器有效降低了系统的体积和重量。作为该光谱仪的核心光学器件，多级微反射镜的阶梯高度一致性、面型平整度和结构精度是决定采样间隔、分辨率和噪声等仪器指标的主要因素。本文提出了基于MOEMS技术的厚度依次减半多层膜法，制作了台阶高度为0.625 μm，阶梯数为32的低阶梯多级微反射镜。测得实际阶梯高度平均值为626.9 nm，表面粗糙度均方根值为1.72 nm。分析了阶梯高度误差对光谱复原的影响，提出了两种阶梯高度误差校正方法，分别为通过修正因子来减小膜厚监控误差，和利用最小二乘余弦多项式算法对复原光谱进行校正。校正后的复原光谱误差(SCE)降低为2.34%，满足系统对光谱复原的要求。最后，将该低阶梯多级微反射镜置入光谱仪中，得到乙腈样品的干涉图和复原光谱图。
-
关键词:
- 傅立叶变换红外光谱仪 /
- 低阶梯多级微反射镜 /
- 高度误差分析
Abstract: In this study, a static and light Fourier transform infrared spectrometer based on stepped mirrors and a grid beam splitter was proposed. By introducing two stepped mirrors into the interference system, the optical path difference is discretized and the 2-dimensional sampling of the interferogram is obtained. Furthermore, by introducing the grid beam splitter into the interference system, the volume and weight are decreased. Stepped mirrors as the core optical devices of such a spectrometer, its step height consistency, face flatness and the structure's precision determine the spectral sampling interval, resolution and noise of the system. We propose a method based on MOEMS technology involving multiple depositions accompanied by a 50% reduction in thickness at every iteration to fabricate a low-stepped mirror with 32 steps and 0.625 μm in step height. The test results show that the root-mean-square of roughness is 1.72 nm and that the average height of the real steps is 626.9 nm. The effect of the height error on the recovered spectrum is analyzed. In order to reduce the influence of this error, two methods are proposed:one is through using tooling factor to reduce the monitoring error of the film thickness, thus reducing the height error; the other is through using the least-squares approximation cosine polynomial algorithm to correct the recovered spectrum. The spectrum-constructing error(SCE) is reduced to 2.34%, which meets the requirements of spectral restoration. Finally, the experiment was carried out using low stepped mirrors and the interferograms were obtained before and after the addition of the sample. The absorption spectrum of the sample acetonitrile can be obtained using a Fourier transform. -
图 3 光谱评价函数SCE随阶梯高度标准差σ变化曲线
Figure 3. SCE varies with height standard deviation σ of the sub-mirror
图 4 低阶梯多级微反射镜制备流程图(以8台阶为例)
Figure 4. Flow diagram of low-stepped multi-level micromirrors(with 8 steps as an example)
图 7 低阶梯多级微反射镜粗糙度测试图
Figure 7. Roughness test chart of low-step multi-level micro-mirrors
图 8 32级低阶梯多级微反射镜台阶高度测试图
Figure 8. Step height test results of low stepped micromirror with 32 steps
图 9 台阶高度测试值与理论值差值图
Figure 9. Step height difference between the measured values and their theoretical values
图 10 使用FFT算法时高度误差影响下的实际光谱和理想复原光谱对比图
Figure 10. Comparison of the ideal spectrum and the actual spectrum using the FFT algorithm with height error
图 11 使用LSC算法时高度误差影响下的实际光谱和理想复原光谱对比图
Figure 11. Comparison of the ideal spectrum and the actual spectrum using the LSC algorithm with height error
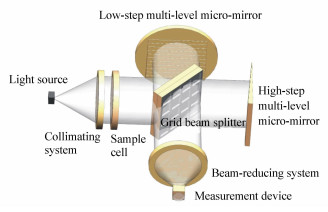
图 12 静态空间调制FTIR原理样机.1光源; 2准直系统; 3样品池; 4栅格分束板和栅格补偿板; 5高阶梯多级微反射镜; 6低阶梯多级微反射镜; 7缩束系统; 8红外探测器
Figure 12. Static spatial modulation FTIR prototype. 1 light source; 2 collimating system; 3 sample chamber; 4 beam splitter and compensation plate; 5 high-stepped micromirror; 6 low-stepped micromirror; 7.constricting system; 8 infrared detector array
图 13 干涉图(a)加入样品前; (b)加入样品后
Figure 13. Interferogram (a)without the sample; (b) with the sample
表 1 Statistical test results of step height
Table 1. Statistical test results of step height
Step Height Value Maximum value/ Highest positive deviation 640/15 Minimum value/Lowest negative value 618/-7 Average value/Average deviation 626.9/1.9 Standard deviation 7.4 
下载: 导出CSV
-
[1] BRACHET F, HÉBERT P J, CANSOT E, et al.. Static Fourier transform spectroscopy breadboards for atmospheric chemistry and climate[J]. Proceedings of SPIE, 2008, 7100:710019. doi: 10.1117/12.797686 [2] REYES D, SCHILDKRAUT E R, KIM J, et al.. A novel method of creating a surface micromachined 3D optical assembly for MEMS-based miniaturized FTIR spectrometers[J]. Proceedings of SPIE, 2008, 6888:68880D. doi: 10.1117/12.764006 [3] SIN J, LEE W H, POPA D, et al.. Assembled Fourier transform micro-spectrometer[J]. Proceedings of SPIE, 2006, 6019:610904. http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC026220616/ [4] 鲍一丹, 陈纳, 何勇, 等.近红外高光谱成像技术快速鉴别国产咖啡豆品种[J].光学 精密工程, 2015, 23(2):349-355. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201502005BAO Y D, CHEN N, HE Y, et al.. Rapid identification of coffee bean variety by near infrared hyperspectral imaging technology[J]. Opt. Precision Eng., 2015, 23(2):349-355.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201502005 [5] 吴伟平, 孙海江.星载紫外环形光谱仪科学数据处理的设计与实现[J].液晶与显示, 2017, 32(5):387-393. http://d.old.wanfangdata.com.cn/Periodical/yjyxs201705010WU W P, SUN H J. Design and realization of data processing of satellite-borne ultraviolet annular imager[J]. Chinese Journal of Liquid Crystals and Displays, 2017, 32(5):387-393.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yjyxs201705010 [6] 王岩, 杨小虎, 王金玲, 等.空间遥感光谱仪器光学性能地面检测系统[J].液晶与显示, 2017, 32(3):206-212. http://d.old.wanfangdata.com.cn/Periodical/yjyxs201703007WANG Y, YANG X H, WANG J L, et al.. Ground testing system for detecting optical performance of space remote sensing spectrometer[J]. Chinese Journal of Liquid Crystals and Displays, 2017, 32(3):206-212.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yjyxs201703007 [7] YAN T Y, ZHANG CH M, LI Q W, et al.. Efficient background removal based on two-dimensional notch filtering for polarization interference imaging spectrometers[J]. Chinese Optics Letters, 2016, 14(12):123002. doi: 10.3788/COL201614.123002 [8] 欧阳爱国, 张宇, 程梦杰, 等.中红外光谱技术对乙醇汽油乙醇含量的检测[J].中国光学, 2017, 10(6):752-759. http://www.chineseoptics.net.cn/CN/abstract/abstract9536.shtmlOUYANG A G, ZHANG Y, CHENG M J, et al.. Determination of the content of ethanol in ethanol gasoline using mid-infrared spectroscopy[J]. Chinese Optics, 2017, 10(6):752-759.(in Chinese) http://www.chineseoptics.net.cn/CN/abstract/abstract9536.shtml [9] FENG C, WANG B, LIANG ZH ZH, et al.. Miniaturization of step mirrors in a static Fourier transform spectrometer:theory and simulation[J]. Journal of the Optical Society of America B, 2011, 28(1):128-133. doi: 10.1364/JOSAB.28.000128 [10] 李志刚.真空紫外分波前傅里叶变换光谱技术进展[J].中国光学, 2015, 8(5):736-743. http://www.chineseoptics.net.cn/CN/abstract/abstract9341.shtmlLI ZH G. Progress of wavefront-division Fourier transform spectrometry in the vacuum ultraviolet[J]. Chinese Optics, 2015, 8(5):736-743.(in Chinese) http://www.chineseoptics.net.cn/CN/abstract/abstract9341.shtml [11] SARDARI B, DAVOLI F, ZCAN M. A broadband configuration for static Fourier transform spectroscopy with bandpass sampling[J]. Review of Scientific Instruments, 2016, 87(10):103106. doi: 10.1063/1.4964473 [12] 李晚侠, 卢启鹏, 宋源, 等.基于双直角分束器的反射式静态傅里叶光谱仪光学系统[J].光学学报, 2017, 37(8):0812004. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201708022LI W X, LU Q P, SONG Y, et al.. Reflective static Fourier transform spectrometer optical system based on double right-angle beam splitter[J]. Acta Optica Sinica, 2017, 37(8):0812004.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201708022 [13] 陈建君, 朱永, 刘波, 等.基于MEMS微镜的傅里叶变换光谱仪原理与分析[J].光谱学与光谱分析, 2012, 32(11):3151-3154. doi: 10.3964/j.issn.1000-0593(2012)11-3151-04CHEN J J, ZHU Y, LIU B, et al.. The principle and analysis of micro-Fourier transform spectrometer based on MEMS micro-mirror[J]. Spectroscopy and Spectral Analysis, 2012, 32(11):3151-3154.(in Chinese) doi: 10.3964/j.issn.1000-0593(2012)11-3151-04 [14] 赵宝玮, 相里斌, 才啟胜, 等.平行双转镜傅里叶变换光谱仪[J].光谱学与光谱分析, 2015, 35(11):3209-3213. http://d.old.wanfangdata.com.cn/Periodical/gpxygpfx201511048ZHAO B W, XIANG L B, CAI Q SH, et al.. Fourier transform spectrometer based on rotating parallel-mirror-pair[J]. Spectroscopy and Spectral Analysis, 2015, 35(11):3209-3213.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gpxygpfx201511048 [15] 廉玉生, 廖宁放, 吕航, 等.一种光谱分辨率可调的新型空间调制傅里叶变换光谱仪[J].光谱学与光谱分析, 2014, 34(11):3136-3140. doi: 10.3964/j.issn.1000-0593(2014)11-3136-05LIAN Y SH, LIAO N F, LV H, et al.. A novel spatial modulation Fourier transform spectrometer with adjustable spectral resolution[J]. Spectroscopy and Spectral Analysis, 2014, 34(11):3136-3140.(in Chinese) doi: 10.3964/j.issn.1000-0593(2014)11-3136-05 [16] ZHENG Y, LIANG J Q, LIANG ZH ZH. Design and fabrication of step mirrors used in space-modulated Fourier transform infrared spectrometer[J]. Optics Express, 2013, 21(1):884-892. doi: 10.1364/OE.21.000884 [17] LACAN A, BRÉON F M, ROSAK A, et al.. A static Fourier transform spectrometer for atmospheric sounding:concept and experimental implementation[J]. Optics Express, 2010, 18(8):8311-8331. doi: 10.1364/OE.18.008311 [18] 梁静秋, 梁中翥, 吕金光, 等.空间调制微型傅里叶变换红外光谱仪研究[J].中国光学, 2015, 8(2):277-298. http://www.chineseoptics.net.cn/CN/abstract/abstract9272.shtmlLIANG J Q, LIANG ZH ZH, LV J G, et al.. Micro spatial modulation Fourier transform infrared spectrometer[J]. Chinese Optics, 2015, 8(2):277-298.(in Chinese) http://www.chineseoptics.net.cn/CN/abstract/abstract9272.shtml [19] CHEN CH, LIANG J Q, LIANG ZH ZH, et al.. Fabrication and analysis of tall-stepped mirror for use in static Fourier transform infrared spectrometer[J]. Optics & Laser Technology, 2015, 75:6-12. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e89de3520160a70085fc6ebf3974d12f [20] 杨道奇, 付秀华, 耿似玉, 等.0.6~1.55μm可见/近红外超宽带增透膜的研制[J].中国光学, 2012, 5(3):270-276. doi: 10.3969/j.issn.2095-1531.2012.03.012YANG D Q, FU X H, GONG S Y, et al.. Design and fabrication of 0.6-1.55μm visible/near infrared ultra-broad band antireflection coatings[J]. Chinese Optics, 2012, 5(3):270-276.(in Chinese) doi: 10.3969/j.issn.2095-1531.2012.03.012 [21] FENG C, LIANG J Q, LIANG ZH ZH. Spectrum constructing with nonuniform samples using least-squares approximation by cosine polynomials[J]. Applied Optics, 2011, 50(34):6377-6383. doi: 10.1364/AO.50.006377 [22] GAO J H, LIANG ZH ZH, LIANG J Q, et al.. Spectrum reconstruction of a spatially modulated Fourier transform spectrometer based on stepped mirrors[J]. Applied Spectroscopy, 2017, 71(6):1348-1356. doi: 10.1177/0003702816669729 -
下载:
图(14) / 表(1)
计量
- 文章访问数: 2255
- HTML全文浏览量: 981
- PDF下载量: 135
- 被引次数: 0
