不同海拔地区红外大气透过率的计算和测量

王飞翔; 郭杰; 许方宇; 张雨辰; 陈双远; 肖建国; 贾钰超; 罗宏; 赵志军

doi:10.3788/CO.20191204.0843

不同海拔地区红外大气透过率的计算和测量

doi: 10.3788/CO.20191204.0843

王飞翔^1,,
郭杰^1, ,,
许方宇^2,,
张雨辰²,
陈双远²,
肖建国³,
贾钰超³,
罗宏³,
赵志军^{2, 4}

1.
云南师范大学云南省光电信息技术重点实验室, 云南昆明 650216
2.
中国科学院云南天文台, 云南昆明 650216
3.
云南北方驰宏光电有限公司, 云南昆明 650217
4.
河南师范大学物理与材料科学学院, 河南新乡 453000

基金项目:

国家自然科学基金资助项目 11803089

详细信息

作者简介:
王飞翔(1995-), 男, 河南驻马店人, 硕士研究生, 主要从事红外辐射方面的研究。E-mail:77902374@qq.com

郭杰(1979-), 男, 云南昆明人, 博士, 副教授, 主要从事红外探测技术的研究。E-mail:ynnugj@sohu.com

许方宇(1972-), 男, 云南昆明人, 博士, 副研究员, 2001年、2006年于天津大学分别获得硕士、博士学位, 主要从事红外天文技术方面的研究。E-mail:xu_fangyu@ynao.ac.cn

中图分类号: O434.3;TN215;P422.6+1
计量
- 文章访问数: 4133
- HTML全文浏览量: 1292
- PDF下载量: 284
- 被引次数: 0
出版历程
- 收稿日期: 2019-01-22
- 修回日期: 2019-03-01
- 刊出日期: 2019-08-01

Calculation and measurement of infrared atmospheric transmittance at different altitudes

1.
Yunnan Key Laboratory of Optoelectronic Information Technology, Yunnan Normal University, Kunming 650216, China
2.
Yunnan Astronomical Observatories, Chinese Academy of Sciences, Kunming 650216, China
3.
Yunnan KIRO-CH Photonics Co. Ltd, Kunming 650217, China
4.
College of Physics and Materials Science, Henan Normal University, Xinxiang 453000, China

Funds:

National Natural Science Foundation of China 11803089

More Information

Corresponding author: GUO Jie, E-mail:ynnugj@sohu.com

摘要

摘要: 为了得到不同海拔地区的大气透过率，探索大气透过率随海拔高度的变化规律，利用数值模拟、软件计算和实地测量方法分别对阿里(5 km)、德令哈(3 km)和怀柔(0 km)3个不同海拔地区在4.605~4.755 μm波段25 km以下的大气透过率进行了计算和测量。结果表明：红外大气透过率随海拔高度增加而增加；采用数值模拟计算得到3个地方的大气透过率分别为0.709、0.572和0.555；采用软件计算得到的透过率分别为0.849、0.766和0.596；采用实测方法得到的透过率分别为0.805、0.766和0.673；阿里地区海拔较高，相对湿度较低，能见度高，大气透过率最好。该结论对国内天文红外观测及空间红外目标辐射特性测量具有重要的借鉴意义。
- 中波红外 /
- 大气透过率 /
- 数值模拟 /
- 海拔高度 /
- 能见度 /
- 辐射测量
Abstract: In order to obtain atmospheric transmittance and study its variation with different altitudes, using methods of mathematical models, software simulations, and actual measurement, we calculate and measure the atmospheric transmittance in the range of 4.605~4.755 μm wavelengths at Ali(5 km), Delingha(3 km) and Huairou(0 km), three different altitudes below 25 km. Results indicate that the infrared atmospheric transmittance increases with altitude. With mathematical model the calculated atmospheric transmittances are 0.709, 0.572 and 0.555, respectively. With software simulations the calculated atmospheric transmittances are 0.849, 0.766 and 0.596, respectively. With actual measurement the obtained atmospheric transmittances are 0.805, 0.766 and 0.673. Due to higher altitude, lower relative humidity, high visibility, the atmospheric transmittance at Ali is the highest one. This conclusion has important reference significance for domestic astronomical infrared observation and spatial infrared target radiation characteristics measurement.
- mid-wavelength infrared /
- atmospheric transmittance /
- numerical simulation /
- altitude /
- visibility /
- radiation measurement

HTML全文

图 1 波长为4.6 μm时水汽含量和平均大气透过率拟合曲线

Figure 1. Fitting curve of the relationship between the content of water vapor and average atmosphere transmittance(when λ is 4.6 μm)

下载: 全尺寸图片幻灯片

图 2 波长为4.6 μm时二氧化碳含量和大气透过率拟合曲线

Figure 2. Fitting curve of the relationship between carbon dioxide content and atmosphere transmittance(when λ is 4.6 μm)

下载: 全尺寸图片幻灯片

图 3 拉萨、都兰县、北京探空数据

Figure 3. The sounding data of Lhasa, Dulan and Beijing

下载: 全尺寸图片幻灯片

图 4 3个地区层数和透过率关系

Figure 4. Relationship between layers and atmospheric transmittance in three regions

下载: 全尺寸图片幻灯片

图 5 MODTRAN模拟3地大气透过率结果

Figure 5. Simulation results of atmospheric transmittances in three regions by MODTRAN

下载: 全尺寸图片幻灯片

图 6 仪器读数随角度变化

Figure 6. Variance of instrument effective readings with zenith angle

下载: 全尺寸图片幻灯片

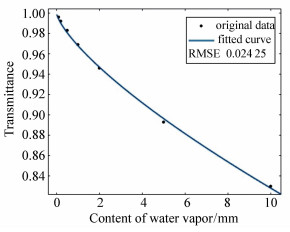
表 1 海平面水汽含量与平均大气透过率的关系(4.6~4.8 μm处)^[11]

Table 1. The relationship between the water vapor content in the sea level and the average atmosphere transmittance(from 4.6~4.8 μm)^[11]

λ/μm	Water vapor content/mm
λ/μm	0.1	0.2	0.5	1.0	2.0	5.0	10.0
4.6	0.996	0.992	0.983	0.969	0.946	0.893	0.830
4.7	0.992	0.985	0.970	0.949	0.916	0.845	0.760
4.8	0.975	0.959	0.926	0.889	0.837	0.733	0.621

下载: 导出CSV

表 2 海平面二氧化碳含量与大气平均透过率的关系(4.6~4.8 μm处)^[14]

Table 2. The relationship between the content of Carbon dioxide in the sea level and the average atmosphere transmittance(from 4.6~4.8 μm)^[14]

λ/nm	Path length/km
λ/nm	0.1	0.2	0.5	1.0	2.0	5.0	10.0	20.0	50.0
4.6	1	1	0.999	0.998	0.996	0.991	0.982	0.969	0.939
4.7	1	0.999	0.996	0.991	0.982	0.955	0.917	0.855	0.719
4.8	0.990	0.981	0.956	0.920	0.865	0.754	0.634	0.486	0.261

下载: 导出CSV

表 3 3个地区大气透过率数值模拟计算结果

Table 3. Calculation results of atmospheric transmittance in three regions with mathematical models

地点	波长/μm	τ_H₂O	τ_CO₂	τ_SC	τ	τ_av
Ali	4.6	0.872	0.982	0.9998	0.857
	4.7	0.743	0.913	0.9998	0.678	0.709
	4.8	0.291	0.028	0.9998	0.008
Delingha	4.6	0.770	0.978	0.9985	0.752
	4.7	0.582	0.894	0.9985	0.519	0.572
	4.8	0.128	0.016	0.9985	0.002
Huairou	4.6	0.804	0.966	0.953	0.740
	4.7	0.625	0.839	0.953	0.500	0.555
	4.8	0.148	0.003	0.953	0.0005

下载: 导出CSV

表 4 3个地方大气透过率结果对照表

Table 4. Comparison of atmospheric transmittance results in three regions

	mathematical model	software simulation	actual measurement
Ali	0.709	0.849	0.805
Delingha	0.572	0.766	0.766
Huairou	0.555	0.596	0.673

下载: 导出CSV

参考文献(16)

[1]	路远, 凌永顺.红外辐射大气透射比的简易计算[J].红外技术, 2003, 25(5):45-49. doi: 10.3969/j.issn.1001-8891.2003.05.012 LU Y, LING Y SH. The simple method to calculate the atmospheric transmittance of infrared radiation[J]. Infrared Technology, 2003, 25(5):45-49.(in Chinese) doi: 10.3969/j.issn.1001-8891.2003.05.012
[2]	宋腾飞, 刘顺庆, 张雪飞.利用日晕光度计反演大气水汽含量[J].气象科技, 2013, 41(1):46-50. doi: 10.3969/j.issn.1671-6345.2013.01.009 SONG T F, LIU SH Q, ZHANG X F. Measurement of total precipitable water in atmosphere with sky brightness monitor[J]. Meteorological Science and Technology, 2013, 41(1):46-50.(in Chinese) doi: 10.3969/j.issn.1671-6345.2013.01.009
[3]	魏合理, 陈秀红, 饶瑞中.通用大气辐射传输软件(CART)介绍[J].大气与环境光学学报, 2007, 2(6):446-450. doi: 10.3969/j.issn.1673-6141.2007.06.006 WEI H L, CHEN X H, RAO R ZH. Introduction to the combined atmospheric radiative transfer software CART[J]. Journal of Atmospheric and Environmental Optics, 2007, 2(6):446-450.(in Chinese) doi: 10.3969/j.issn.1673-6141.2007.06.006
[4]	WALDEN V P, TOWN M S, HALTER B, et al.. First measurements of the infrared sky brightness at dome C, antarctica[J]. Publications of the Astronomical Society of the Pacific, 2005, 117(829):300-308. doi: 10.1086/427988
[5]	王浩, 何枫, 靖旭, 等.昼夜观测恒星整层大气透过率测量研究[EB/OL].(2018-10-30)[2018.11.20] http://kns.cnki.net/kcms/detail/12.1261.TN.20181029.0846.014.html. WANG H, HE F, JING X, et al.. Study on measurement of total atmospheric transmittance in daytime and night observation stars[EB/OL].(2018-10-30)[2018.11.20].http://kns.cnki.net/kcms/detail/12.1261.TN.20181029.0846.014.html.(in Chinese)
[6]	BHATTACHARYYA J C, SCARIAKK, SINGH J, et al. Atmospheric extinction measurements at Leh in near infrared bands[J]. Bulletin of the Astronomical Society of India, 1990, 18(18):1-6.
[7]	LIOUKN, BOHRENC. An introduction to atmospheric radiation[J]. Physics Today, 1981, 34(7):66-67. doi: 10.1063/1.2914664
[8]	赵志军, 许方宇, 魏超群, 等.红外整层大气透过率测量方法研究[J].红外技术, 2018, 40(7):718-722. http://d.old.wanfangdata.com.cn/Periodical/hwjs201807017 ZHAO ZH J, XU F Y, WEI CH Q, et al.. Study on measurement method for total infrared atmospheric transmittance[J]. Infrared Technology, 2018, 4(7):718-722.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hwjs201807017
[9]	陈双远, 许方宇, 王飞翔, 等.中红外大气背景辐射测量设备及误差分析[J].光学学报, 2019, 39(3):0301001. CHEN SH Y, XU F Y, WANG F X, et al.. Measurement equipment and error analysis of mid-infrared atmospheric background radiation[J]. Acta Optica Sinica, 2019, 39(3).(in Chinese)
[10]	康大勇, 成斌, 高俊光.地空红外探测距离推算方法探讨[J].光电技术应用, 2009, 24(1):29-32. doi: 10.3969/j.issn.1673-1255.2009.01.008 KANG D Y, CHENG B, GAO J G. Differentiation algorithm method of ground-air infrared detection range[J]. Electro-Optic Technology Appliction, 2009, 24(1):29-32.(in Chinese) doi: 10.3969/j.issn.1673-1255.2009.01.008
[11]	刘林华, 董士奎, 余其铮, 等.红外1~14μm波长间隔0.1μm上大气平均透过率(Ⅱ)水蒸汽的透过率[J].哈尔滨工业大学学报, 1999, 31(6):75-78. LIU L H, DONG SH K, YU Q ZH, et al.Atmospheric mean transmittance in wavelength interval 0.1μm from infrared 1 to 14μm, (Ⅱ) transmittance of water vapor[J]. Journal of Harbin Institute of Technology, 1999, 31(6):75-78. (in Chinese)
[12]	ZHANG Y C, CHEN Y M, FU X B, et al.. The research on the effect of atmospheric transmittance for the measuring accuracy of infrared thermal imager[J]. Infrared Physics & Technology, 2016, 77:375-381.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=76ccaf8ddb2ba7c78451c29152e5cbf4
[13]	张建奇, 方小平.红外物理[M].西安:西安电子科技大学出版社, 2007. ZHANG J Q, FANG X P. Infrared Physics[M]. Xian:Xidian University Press, 2007.(in Chinese)
[14]	刘林华, 董士奎, 余其铮, 等.红外1~14μm波长间隔0.1μm上大气平均透过率(Ⅰ)二氧化碳的透过率[J].哈尔滨工业大学学报, 1998, 30(5):8-12. LIU L H, DONG SH K, YU Q ZH, et al.. Atmospheric mean transmittance in wavelength interval 0.1μm from infrared 1 to 14μm, (Ⅰ) transmittance of carbon dioxide[J]. Journal of Harbin Institute of Technology, 1998, 30(5):8-12.(in Chinese)
[15]	赵志军, 许方宇, 高玲, 等.3~5μm红外天空亮度测量的多元定标模型[J].红外与激光工程, 2017, 46(10):1004004. http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201710038 ZHAO ZH J, XU F Y, GAO L, et al.. Multivariate calibration model for measurement of 3-5μm infrared sky brightness[J]. Infrared and Laser Engineering, 2017, 46(10):1004004.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201710038
[16]	赵志军, 许方宇, 徐世春, 等.大气红外辐射及消光特性实测研究[J].光学学报, 2018, 38(4):0401004-4-5. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201804004 ZHAO ZH J, XU F Y, XU SH CH, et al.. Measurement of atmospheric infrared radiance and extinction characteristics[J]. Acta Optica Sinica, 2018, 38(4):0401004-4-5.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201804004