Coherent free-space optical communication system with quadrature phase-shift keying modulation using a digital phase recovery algorithm
-
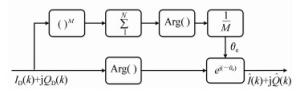
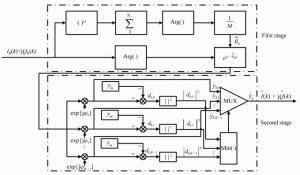
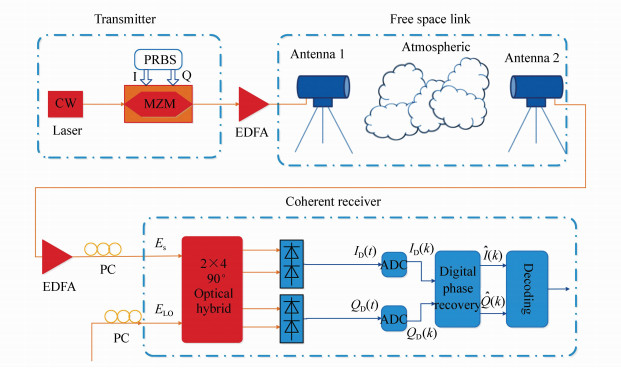
摘要: 近年来,大气湍流所引起的信号相位扰动以及光强闪烁对自由空间相干光通信系统性能的影响逐渐成为研究人员关注的焦点。为了提高系统性能,本文对自由空间相干光通信系统进行了研究。在假设大气湍流所引入的光强闪烁以及相位抖动分别服从对数正态以及高斯分布的条件下,本文提出了基于数字相位恢复算法(CPR)的正交相移键控(QPSK)自由空间相干光通信系统,该系统采用了二阶联合的相位恢复算法结构。仿真结果表明:该结构可以极大地降低相位噪声对系统产生的影响,且其误符号率比只采用一阶M次方的相位恢复算法的系统低3个数量级。因此,该系统的提出对于自由空间光通信性能的提升有着较大意义。Abstract: In recent years, the dilemma regarding the limited performance of coherent free-space optical(CFSO) communication with phase modulation caused by the phase fluctuations and intensity scintillations associated with atmospheric turbulence has gradually become the focus of research. In order to improve system performance, a CFSO communication system with quadrature phase-shift keying modulation(QPSK) is studied in this paper. With consideration of log-normal amplitude fluctuations and Gaussian distribution conditions, a two-stage joint carrier phase recovery(CPR) algorithm is proposed. With this scheme, the simulation results show that the phase noise of the system can be greatly reduced and its symbol error rate is three orders lower than that of the single-stage M-th power CPR algorithm. Therefore, the two-stage joint CPR algorithm holds significant improvement in CFSO communication systems.
-
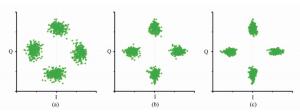
图 4 激光器线宽为100kHz时的星座图.(a)相位校正前, (b)单阶相位校正, (c)双阶联合相位校正后
Figure 4. Normalized constellation diagram of QPSK signal with laser linewidth of 100 kHz for the transmitter and the local oscillator. (a)Before using carrier phase recovery algorithm, (b)after using single-stage carrier phase recovery algorithm, and (c)after using two-stage joint carrier phase recovery algorithm
图 5 激光器线宽为100 kHz,频偏为20 MHz时的星座图. (a)相位校正前, (b)单阶相位校正后, (c)双阶联合相位校正后
Figure 5. Normalized constellation diagram of QPSK signal with laser linewidth of 100 kHz and frequency offset of 20 MHz for the transmitter and the local oscillator. (a)Before using carrier phase recovery algorithm, (b)after using single-stage carrier phase recovery algorithm, and (c)after using two-stage joint carrier phase recovery algorithm
表 1 仿真参数
Table 1. Simulation parameters
参数设置 Value 波长 1 550 nm 接收口径D 5 cm 折射率结构常数Cn2 1.5×10-15 m-2/3 相干长度r0 24.5 cm 传输距离L 1 000 m 里托夫方差σR 0.17 相位方差σϕ 0.07 rad -
[1] HOU L F, ZHANG L, KIM J. Energy modeling and power measurement for mobile robots[J]. Energies, 2019, 12(1):27. [2] 马爽, 吴志勇, 高世杰, 等.改进的大气激光通信PPM调制解调系统设计[J].哈尔滨工业大学学报, 2016, 48(5):105-109. http://d.old.wanfangdata.com.cn/Periodical/hebgydxxb201605018MA SH, WU ZH Y, GAO SH J, et al.. Design of modified atmospheric laser communication PPM modulation-demodulation system[J]. Journal of Harbin Institute of Technology, 2016, 48(5):105-109.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hebgydxxb201605018 [3] 宋少华, 仝召民.用于激光背光源电视的扫描分光与消散斑系统[J].光学 精密工程, 2019, 27(2):271-278. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201902001SONG SH H, TONG ZH M. Scanning beam splitting and speckle reduction system for laser backlight TV[J]. Opt. Precision Eng., 2019, 27(2):271-278.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201902001 [4] 吴伟辉, 杨永强, 毛桂生, 等.激光选区熔化自由制造异质材料零件[J].光学 精密工程, 2019, 27(3):517-526. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201903002WU W H, YANG Y Q, MAO G SH, et al.. Free manufacturing of heterogeneous materials part by selective laser melting[J]. Opt. Precision Eng., 2019, 27(3):517-526.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201903002 [5] LI X L, GENG T W, MA SH, et al.. Performance improvement of coherent free-space optical communication with quadrature phase-shift keying modulation using digital phase estimation[J]. Applied Optics, 2017, 56(16):4695-4701. doi: 10.1364/AO.56.004695 [6] LI L, GENG T W, WANG Y, et al.. Free-space optical communication using coherent detection and double adaptive detection thresholds[J]. IEEE Photonics Journal, 2019, 11(1):7900217. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e6275320c1ba777016b5b267317ce864 [7] 涂焱阳, 吴志勇, 马爽, 等.阈值可变的高速光通信脉冲位置调制的帧同步[J].中国激光, 2017, 44(11):106008. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201711027TU Y Y, WU ZH Y, MA SH, et al.. Frame synchronization of pulse position modulation in high-speed optical communication with variable threshold[J]. Chinese Lasers, 2017, 44(11):106008.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201711027 [8] LI Y T, GUO S A, GENG T W, et al.. Evaluation on the capacity and outage performance of the free space optical system impaired by timing jitters over an aggregate channel[J]. Optical Engineering, 2017, 56(7):076108. doi: 10.1117/1.OE.56.7.076108 [9] 徐春凤, 倪小龙, 刘智.激光大气湍流传输中的光强闪烁特性[J].光学 精密工程, 2016, 24(10s):183-189. http://www.eope.net/gxjmgc/CN/abstract/abstract16628.shtmlXU CH F, NI X L, LIU ZH. Scintillation in turbulent atmosphere laser communication[J]. Opt. Precision Eng., 2016, 24(10s):183-189.(in Chinese) http://www.eope.net/gxjmgc/CN/abstract/abstract16628.shtml [10] 谢伟良, 汤俊雄.基于Turbo码的大气无线光通信系统特性分析[J].中国激光, 2003, 30(9):835-838. doi: 10.3321/j.issn:0258-7025.2003.09.015XIE W L, TANG J X. Analysis on characterization of atmospheric optical wireless communication system based on turbo code[J]. Chinese Lasers, 2003, 30(9):835-838.(in Chinese) doi: 10.3321/j.issn:0258-7025.2003.09.015 [11] 高宠, 马晶, 谭立英, 等.大气光通信中大气闪烁时间平滑效应研究[J].光学学报, 2006, 26(4):481-486. doi: 10.3321/j.issn:0253-2239.2006.04.001GAO CH, MA J, TAN L Y, et al.. Time-averaging effects for atmospheric scintillation in atmospheric optical communication[J]. Acta Optica Sinica, 2006, 26(4):481-486.(in Chinese) doi: 10.3321/j.issn:0253-2239.2006.04.001 [12] 陈纯毅, 杨华民, 姜会林, 等.大气光通信中大气湍流影响抑制技术研究进展[J].兵工学报, 2009, 30(6):779-791. doi: 10.3321/j.issn:1000-1093.2009.06.022CHEN CH Y, YANG H M, JIANG H L, et al.. Research progress of mitigation technologies of turbulence effects in atmospheric optical communication[J]. Acta Armamentarii, 2009, 30(6):779-791.(in Chinese) doi: 10.3321/j.issn:1000-1093.2009.06.022 [13] IP E, KAHN J M. feedforward carrier recovery for coherent optical communications[J]. Journal of Lightwave Technology, 2005, 23(9):2675-2692. https://www.osapublishing.org/jlt/abstract.cfm?uri=jlt-25-9-2675 [14] LI X, CAO Y W, YU S, et al.. A simplified feedforward carrier recovery algorithm for coherent optical QAM system[J]. Journal of Lightwave Technology, 2011, 29(5):801-807. doi: 10.1109/JLT.2011.2106197 [15] VITERBI A. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission[J]. IEEE Transactions on Information Theory, 1983, 29(4):543-551. https://ieeexplore.ieee.org/document/1056713 [16] LI M, CVIJETIC M. Coherent free space optics communications over the maritime atmosphere with use of adaptive optics for beam wavefront correction[J]. Applide Optics, 2015, 54(6):1453-1462. doi: 10.1364/AO.54.001453 [17] NOLL R J. Zernike polynomials and atmospheric turbulence[J]. Journal of the Optical Society of America, 1976, 66(3):207-211. doi: 10.1364/JOSA.66.000207 [18] FRIED D L. Optical heterodyne detection of an atmospherically distorted signal wave front[J]. Proceedings of the IEEE, 1967, 55(1):57-77. doi: 10.1109/PROC.1967.5377 [19] FRIED D L. Optical resolution through a randomly inhomogeneous medium for very long and very short exposures[J]. Journal of the Optical Society of America, 1966, 56(10):1372-1379. doi: 10.1364/JOSA.56.001372 [20] FRIED D L. Optical heterodyne detection of an atmospherically distorted signal wave front[J]. Proceedings of the IEEE, 1967, 55(1):57-77. doi: 10.1109/PROC.1967.5377 [21] BELMONTE A, KAHN J M. Capacity of coherent free-space optical links using diversity-combining techniques[J]. Optics Express, 2009, 17(15):12601-12611. doi: 10.1364/OE.17.012601 [22] LY-GAGNON D S, TSUKAMOTO S, KATOH K, et al. Coherent detection of optical quadrature phase-shift keying signals with carrier phase estimation[J]. Journal of Lightwave Technology, 2006, 24(1):12-21. doi: 10.1109/JLT.2005.860477 -






 下载:
下载: