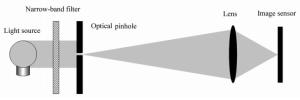
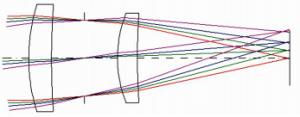
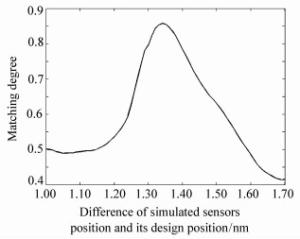
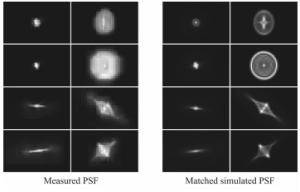
-
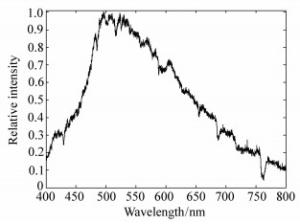
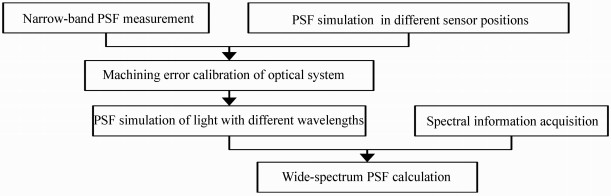
摘要: 为了准确获取简单光学系统的点扩散函数(PSF),提升图像复原质量,本文提出了一种基于PSF测量的宽光谱PSF估计方法。首先,测量了光学系统的窄带PSF,并结合图像匹配算法,标定了实际光学系统中的探测器位置和光轴中心偏移。然后,模拟实际光学系统各波长、各视场的PSF,再结合目标反射光谱和探测器光谱敏感信息计算实际目标的宽光谱PSF。实验结果表明:本文提出的PSF估计方法明显优于窄带PSF估计和盲估计方法,复原图片质量和稳定性均有明显提升,能够准确估计实际光学成像系统的PSF。Abstract: In order to obtain point spread functions(PSFs) of a simple optical system accurately and improve the restored image quality, we present a wide-spectrum PSF estimation method based on PSF measurements. First, narrow-band PSFs are measured, and combining image matching algorithm, the sensor position and the deviation of the optical axis in the real optical system are calibrated. Then, the PSF of each wavelength and field of view is simulated and used for calculating the wide-spectrum PSFs of the real optical system according to the object reflectance spectrum and the spectral sensitivity information of the sensor. Experimental results indicate that the proposed PSF estimation method is better than the narrow-band PSF estimation and blind PSF estimation. The restored image is more stable and its quality is improved significantly. The proposed method can estimate the PSFs of the real optical imaging system accurately.
-
Key words:
- computational imaging /
- point spread function /
- image restoration /
- wide spectrum
-
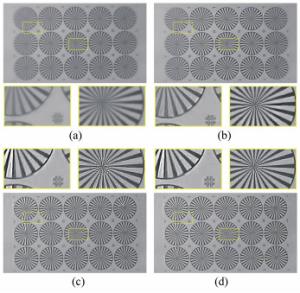
图 9 “卫星”图像[18]复原结果对比。(a)模糊图;(b)Krishnan盲估PSF复原结果;(c)单波长PSF复原结果;(d)本文估计PSF的复原结果
Figure 9. Comparison of restored results for "satellite" image[18]. (a)Blurred image, (b)restored results of Krishnan′s blind-estimated PSF, (c)restored results of single-wavelength PSF and (d)restored results of proposed method
表 1 自制简单相机的镜头参数
Table 1. Lens parameters of the self-designed simple camera
Surface Radius Thickness Glass Object Infinity Infinity 1 31.84 4.00 HK9L_CDGM 2 125.56 5.80 stop Infinity 5.80 4 21.29 3.50 HK9L_CDGM 5 109.53 25.42 Image Infinity 0 表 2 图像灰度平均梯度对比
Table 2. Comparison of image grayscale mean gradients
Satellite Target Blurred image 0.002 4 0.003 1 Krishnan et al. 0.006 9 0.008 5 Using 532 nm PSF 0.108 0 0.013 1 Ours 0.109 0 0.014 1 -
[1] 杨利红, 赵变红, 张星祥, 等.点扩散函数高斯拟合估计与遥感图像恢复[J].中国光学, 2012, 5(2):181-188. doi: 10.3969/j.issn.2095-1531.2012.02.014YANG L H, ZHAO B H, ZHANG X X, et al.. Gaussian fitted estimation of point spread function and remote sensing image restoration[J]. Chinese Optics, 2012, 5(2):181-188.(in Chinese) doi: 10.3969/j.issn.2095-1531.2012.02.014 [2] 常松涛, 孙志远, 张尧禹, 等.基于点扩散函数的小目标辐射测量[J].光学 精密工程, 2014, 22(11):2879-2887. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201411001CHANG S T, SUN ZH Y, ZHANG Y Y, et al.. Radiation measurement of small targets based on PSF[J]. Opt. Precision Eng., 2014, 22(11):2879-2887.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201411001 [3] KRISHNAN D, TAY T, FERGUS R. Blind deconvolution using a normalized sparsity measure[C]. Proceedings of the 2011 Computer Vision and Pattern Recognition, IEEE, 2011, 42: 233-240. [4] SCHULER C J, HIRSCH M, HARMELING S, et al.. Blind correction of optical aberrations[C]. Proceedings of the European Conference on Computer Vision, Springer, 2012: 187-200. [5] 郭从洲, 秦志远.非凸高阶全变差正则化自然光学图像盲复原[J].光学 精密工程, 2015, 23(12):3490-3499. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201512027GUO C ZH, QIN ZH Y. Blind restoration of nature optical images based on non-convex high order total variation regularization[J]. Opt. Precision Eng., 2015, 23(12):3490-3499.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201512027 [6] 闫敬文, 彭鸿, 刘蕾, 等.基于L0正则化模糊核估计的遥感图像复原[J].光学 精密工程, 2014, 22(9):2572-2579. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201409037YAN J W, PENG H, LIU L, et al.. Remote sensing image restoration based on zero-norm regularized kernel estimation[J]. Opt. Precision Eng., 2014, 22(9):2572-2579.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201409037 [7] KEE E, PARIS S, HEN S, et al.. Modeling and removing spatially-varying optical blur[C]. Proceedings of the 2011 IEEE International Conference on Computational Photography, IEEE, 2011: 1-8. [8] BRAUERS J, SEILER C, AACH T. Direct PSF estimation using a random noise target[J]. Proceedings of SPIE, 2010, 7537:75370B. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0210191959 [9] HEIDE F, ROUF M, HULLIN M B, et al.. High-quality computational imaging through simple lenses[J]. ACM Transactions on Graphics, 2013, 32(5):149. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0231441120/ [10] 郝玲.基于空变系统图像恢复的点扩散函数获取研究[D].哈尔滨: 哈尔滨工业大学, 2012.HAO L. Point spread function obtaining research based on the linear space variant image restoration[D]. Harbin: Harbin Institute of Technology, 2012.(in Chinese) [11] ZHENG Y D, HUANG W, PAN Y, et al.. Optimal PSF estimation for simple optical system using a wide-band sensor based on PSF measurement[J]. Sensors, 2018, 18(10):3552. doi: 10.3390/s18103552 [12] 陈新华, 季轶群, 沈为民, 等.基于星点图像的小像差复原[J].光学 精密工程, 2012, 20(4):706-711. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201204004CHEN X H, JI Y Q, SHEN W M, et al.. Small-aberration retrieval based on spot images[J]. Opt. Precision Eng., 2012, 20(4):706-711.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201204004 [13] SIMPKINS J D, STEVENSON R L. A spatially varying PSF model for Seidel aberrations and defocus[J]. Proceedings of SPIE, 2013, 8666:86660F. doi: 10.1117/12.2008851 [14] WANG CH, HEN J, JIA H G, et al.. Parameterized modeling of spatially varying PSF for lens aberration and defocus[J]. Journal of the Optical Society of Korea, 2015, 19(2):136-143. doi: 10.3807/JOSK.2015.19.2.136 [15] SHIH Y, GUENTER B, JOSHI N. Image enhancement using calibrated lens simulations[C]. Proceedings of the European Conference on Computer Vision, Springer, 2012, 7575: 42-56. [16] GONZALEZ R C, WOODS R E. Digital Image Processing[M]. 3rd ed.India:Prentice Hall, 2008. [17] KRISHNAN D, FERGUS R. Fast image deconvolution using hyper-Laplacian priors[C]. Proceedings of the 22nd International Conference on Neural Information Processing Systems, Curran Associates Inc., 2009: 1033-1041. [18] ALMEIDA M S C, ALMEIDA L B. Blind and semi-blind deblurring of natural images[J]. IEEE Transactions on Image Processing, 2010, 19(1):36-52. doi: 10.1109-TIP.2009.2031231/ -






 下载:
下载: