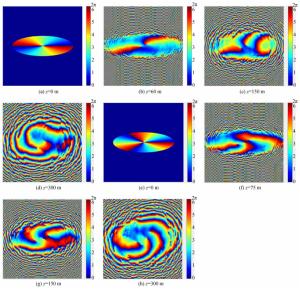
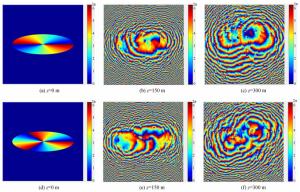
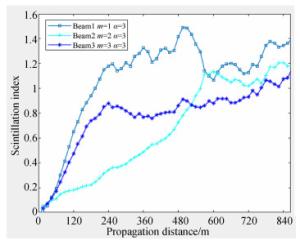
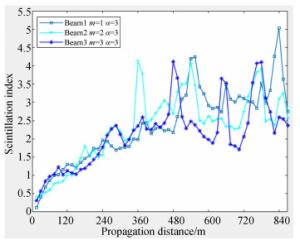
-
摘要: 本文采用分步相位屏方法来仿真椭圆涡旋光束在海洋中的实际传输情况，并对椭圆涡旋光束在海洋湍流中的传输光强和闪烁因子进行了仿真。研究发现，椭圆涡旋光束在海洋传输过程中，光斑会发生明显的旋转，同时光斑会产生暗核且暗核个数与光束的拓扑荷数相等。一个拓扑荷数为m的相位奇点会分裂成m个拓扑荷数为1的相位奇点，并且海洋湍流越强，光斑受到的干扰越严重。研究还发现，在较弱的海洋湍流中，随着传输距离的增加，椭圆涡旋光束的闪烁因子会低于高斯光束和涡旋光束的闪烁因子，而且在远距离处拓扑荷数越大闪烁因子降低越明显，同时也发现，传播一段距离后涡旋光束的闪烁因子会低于高斯光束的闪烁因子。在较强湍流中，椭圆涡旋光束的闪烁因子会交叠在一起。对于不同强度的海洋湍流，随着均方温度耗散率的增大，椭圆涡旋光束的轴上点闪烁因子也增大。在同一传输距离处，束腰宽度越小的椭圆涡旋光束闪烁因子越小。Abstract: The propagation and scintillation index of elliptical vortex beams propagating in oceanic turbulence were simulated using a step-by-step phase screen method.It was found that the beam spot rotates significantly when an elliptical vortex beam transmits through the oceanic turbulence and dark cores are produced, whose number is equal to the topological charge of the beam. A phase singularity with the topological charge m splits into m phase singularities with 1 unit of topological charge and as oceanic turbulence is made stronger, the beam spot experiences greater distortion. It was also found that with an increment in propagation distance, the scintillation index of the elliptical vortex beam is lower than that of the Gaussian beam and the vortex beam in weaker ocean turbulence.Likewise, it was found that the scintillation index reduces more evidently with a larger topological charge when the elliptical vortex beam propagates over a longer distance and that the scintillation index of the vortex beam is lower than that of Gaussian beam after a given transmission distance. In stronger oceanic turbulence, the scintillation indices of the elliptical vortex beams overlap. For oceanic turbulence of different strength, the on-axis scintillation index of the elliptical vortex beam increases with an increment in the rate of dissipation of the mean-square temperature. At a constant propagation distance, a smaller elliptical vortex beam waist width corresponds to a smaller scintillation index.
-
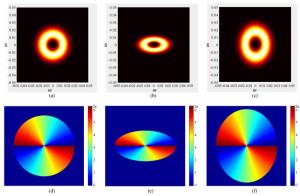
图 1 m=2时不同椭球率的椭圆涡旋光束的光强分布和相应的相位分布，其中(a)、(b)、(c)的椭球率分别为1、2、5/6，(d)、(e)、(f)为其相应的相位分布
Figure 1. Intensity distributions and phase distributions of elliptical vortex beams with m=2 under different ellipsoid ratios, where (a), (b) and (c) have ellipsoid ratios of 1, 2 and 5/6 respectively, and (d), (e) and (f) are corresponding phase distributions
图 2 拓扑荷数m=2(a)~(d)及m=3(e)~(h)的椭圆涡旋光束在较弱的海洋湍流中传输到不同距离处的光强分布
Figure 2. Intensity distributions of elliptical vortex beams with m=2(a)~(d) and m=3(e)~(h) propagating in weaker oceanic turbulence at different propagation distances
图 3 拓扑荷数m=2(a)~(d)及m=3(e)~(h)的椭圆涡旋光束在较弱的海洋湍流中传输到不同距离处的相位分布
Figure 3. Phase distributions of elliptical vortex beams with m=2(a)~(d) and m=3(e)~(h) propagating in weaker oceanic turbulence at different propagation distance
图 4 拓扑荷数m=2(a)~(c)及m=3(d)~(f)的椭圆涡旋光束在较强的海洋湍流中传输到不同距离处的光强分布
Figure 4. Intensity distributions of elliptical vortex beams with m=2(a)~(c) and m=3(d)~(f) propagating in stronger oceanic turbulence at different propagation distances
图 5 拓扑荷数m=2(a)~(c)及m=3(d)~(f)的椭圆涡旋光束在较强的海洋湍流中传输到不同距离处的相位分布
Figure 5. Phase distributions of elliptical vortex beams with m=2(a)~(c) and m=3(d)~(f) propagating in stronger oceanic turbulence at different propagation distances
图 6 高斯光束、涡旋光束和椭圆涡旋光束在较弱的海洋湍流中传输的轴上点的闪烁因子
Figure 6. On-axis scintillation indices of Gaussian beams、vortex beams and elliptical vortex beams propagating in weaker oceanic turbulence
图 7 不同拓扑荷数的椭圆涡旋光束在较弱海洋湍流中传输的轴上点的闪烁因子
Figure 7. On-axis scintillation indices of elliptical vortex beams with different topological charges propagating in weaker oceanic turbulence
图 8 不同拓扑荷数的椭圆涡旋光束在较强的海洋湍流中传输的轴上点的闪烁因子
Figure 8. On-axis scintillation indices of elliptical vortex beams with different topological charges propagating in stronger oceanic turbulence
图 9 不同束腰宽度下的m=2的椭圆涡旋光束在较弱海洋湍流中传输的轴上点的闪烁因子
Figure 9. On-axis scintillation indices of elliptical vortex beams with m=2 at different waist widthes propagating in weaker oceanic turbulence
-
[1] YI X, LI Z, LIU Z J. Underwater optical communication performance for laser beam propagation through weak oceanic turbulence[J]. Applied Optics, 2015, 54(6):1273-1278. doi: 10.1364/AO.54.001273 [2] WOJTANOWSKI J, MIERCZYK Z, ZYGMUNT M. Laser remote sensing of underwater objects[J]. Proceedings of SPIE, 2008, 7105:71050F. http://cn.bing.com/academic/profile?id=9626799cad6ccad8b54883a9c8d49e1b&encoded=0&v=paper_preview&mkt=zh-cn [3] NIKISHOV V V, NIKISHOV V I. Spectrum of turbulent fluctuations of the sea-water refraction index[J]. International Journal of Fluid Mechanics Research, 2000, 27(1):82-98. doi: 10.1615/InterJFluidMechRes.v27.i1.70 [4] 尹霄丽, 郭翊麟, 闫浩, 等.汉克-贝塞尔光束在海洋湍流信道中的螺旋相位谱分析[J].物理学报, 2018, 67(11):114201. doi: 10.7498/aps.67.20180155YIN X L, GUO Y L, YAN H, et al..Analysis of orbital angular momentum spectra of Hankel-Bessel beams in channels with oceanic turbulence[J]. Acta Physica Sinica, 2018, 67(11):114201. (in Chinese) doi: 10.7498/aps.67.20180155 [5] FU W Y, ZHANG H M. Propagation properties of partially coherent radially polarized doughnut beam in turbulent ocean[J]. Optics Communications, 2013, 304:11-18. doi: 10.1016/j.optcom.2013.03.029 [6] CHENG M J, GUO L X, LI J T, et al..Propagation of an optical vortex carried by a partially coherent Laguerre-Gaussian beam in turbulent ocean[J]. Applied Optics, 2016, 55(17):4642-4648. doi: 10.1364/AO.55.004642 [7] CHEN X D, ZHAO D M. Propagation properties of electromagnetic rectangular multi-Gaussian Schell-model beams in oceanic turbulence[J]. Optics Communications, 2016, 372:137-143. doi: 10.1016/j.optcom.2016.03.082 [8] LU CH Y, ZHAO D M. Propagation of electromagnetic multi-Gaussian Schell-model beams with astigmatic aberration in turbulent ocean[J]. Applied Optics, 2016, 55(29):8196-8200. doi: 10.1364/AO.55.008196 [9] FARWELL N, KOROTKOVA O. Intensity and coherence properties of light in oceanic turbulence[J]. Optics Communications, 2012, 285(6):872-875. doi: 10.1016/j.optcom.2011.10.020 [10] KOROTKOVA O, FARWELL N, SHCHEPAKINA E. Light scintillation in oceanic turbulence[J]. Waves in Random and Complex Media, 2012, 22(2):260-266. doi: 10.1080/17455030.2012.656731 [11] 牛超君, 卢芳, 韩香娥.相位屏法模拟高斯阵列光束海洋湍流传输特性[J].光学学报, 2018, 38(6):0601004. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201806004NIU CH J, LU F, HAN X E. Propagation properties of Gaussian array beams transmitted in oceanic turbulence simulated by phase screen method[J]. Acta Optica Sinica, 2018, 38(6):0601004. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201806004 [12] 娄岩, 陈纯毅, 赵义武, 等.高斯涡旋光束在大气湍流传输中的特性研究[J].中国光学, 2017, 10(6):768-776. doi: 10.3788/CO.20171006.0768LOU Y, CHEN CH Y, ZHAO Y W, et al..Characteristics of Gaussian vortex beam in atmospheric turbulence transmission[J]. Chinese Optics, 2017, 10(6):768-776. (in Chinese) doi: 10.3788/CO.20171006.0768 [13] 李波, 王挺峰, 王弟男, 等.激光大气传输湍流扰动仿真技术[J].中国光学, 2012, 5(3):289-295. doi: 10.3969/j.issn.2095-1531.2012.03.015LI B, WANG T F, WANG D N, et al..Simulation of laser beam propagation through turbulence[J]. Chinese Optics, 2012, 5(3):289-295. (in Chinese) doi: 10.3969/j.issn.2095-1531.2012.03.015 [14] 赵云峰, 李夜金, 张寅, 等.海洋背景下运动目标的天基红外探测场景生成系统[J].光学 精密工程, 2017, 25(4):1019-1025. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201704025ZHAO Y F, LI Y J, ZHANG Y, et al..A space-based infrared detection scene generation system for moving objects with sea background[J]. Opt. Precision Eng., 2017, 25(4):1019-1025. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201704025 [15] 刘超, 陈善球, 廖周, 等.自适应光学技术在通信波段对大气湍流的校正[J].光学 精密工程, 2014, 22(10):2605-2610. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxjmgc201410004LIU CH, CHEN SH Q, LIAO ZH, et al..Correction of atmospheric turbulence by adaptive optics in waveband of free-space coherent laser communication[J]. Opt. Precision Eng., 2014, 22(10):2605-2610. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxjmgc201410004 [16] LIU X H, PU J X. Investigation on the scintillation reduction of elliptical vortex beams propagating in atmospheric turbulence[J]. Optics Express, 2011, 19(27):26444-26450. doi: 10.1364/OE.19.026444 [17] YE F, ZHANG J B, XIE J T, et al..Propagation properties of the rotating elliptical chirped Gaussian vortex beam in the oceanic turbulence[J]. Optics Communications, 2018, 426:456-462. doi: 10.1016/j.optcom.2018.05.077 [18] ZHANG J B, XIE J T, YE F, et al..Effects of the turbulent atmosphere and the oceanic turbulence on the propagation of a rotating elliptical Gaussian beam[J]. Applied Physics B, 2018, 124(8):168. doi: 10.1007/s00340-018-7038-2 [19] 刘永欣, 陈子阳, 蒲继雄.随机电磁高阶Bessel-Gaussian光束在海洋湍流中的传输特性[J].物理学报, 2017, 66(12):124205. doi: 10.7498/aps.66.124205LIU Y X, CHEN Z Y, PU J X. Propagation of stochastic electromagnetic high-order Bessel-Gaussian beams in the oceanic turbulence[J]. Acta Physica Sinica, 2017, 66(12):124205. (in Chinese) doi: 10.7498/aps.66.124205 [20] XIAO X F, KOROTKOVA O, VOELZ D G. Laboratory investigation of the spectral exponent effect on scintillation in non-kolmogorov turbulence[C]. Proceedings of 2014 Imaging and Applied Optics, OSA, 2014: PM3E.3. [21] KOTLYAR V V, KHONINA S N, ALMAZOV A A, et al..Elliptic Laguerre-Gaussian beams[J]. Journal of the Optical Society of America A, 2006, 23(1):43-56. doi: 10.1364/JOSAA.23.000043 [22] LIU Y X, ZHANG K N, CHEN Z Y, et al..Scintillation index of double vortex beams in turbulent atmosphere[J]. Optik, 2019, 181:571-574. doi: 10.1016/j.ijleo.2018.12.046 -
下载:
计量
- 文章访问数: 2036
- HTML全文浏览量: 923
- PDF下载量: 155
- 被引次数: 0
