Analysis of thermal drift in high performance interferometric fiber-optic gyroscopes
-
摘要: 为了改进干涉式光纤陀螺的测量精度和温度性能,建立了该仪器输出偏置的解析模型。通过把光纤双折射这一从未被考察过的相位微扰与其它已知误差源进行线性叠加,该模型首次显式地把陀螺性能直接与光纤的力学、光学、热学和几何参数联系起来。利用该模型对常用于10-3 deg/h精度量级光纤陀螺的64层四极对称环圈进行计算,结果表明,保偏光纤所固有的高双折射及其温度涨落对陀螺输出偏置及其热漂移的影响分别在10-3 deg/h和10-2 deg/h量级,而过去研究较多的单模光纤中的舒普效应和热致光弹效应的影响分别在10-4 deg/h和10-3 deg/h量级。该模型表明保偏光纤所固有的高应力双折射是干涉式光纤陀螺的主要误差源,同时较为完备地描述了光纤陀螺中源于光纤性能的误差,也解释了该误差对光纤双折射的非线性依赖。Abstract: In order to improve accuracy and thermal performance, an analytical model of thermal-induced drift in interferometric fiber-optic gyroscopes containing all of the known phase perturbations is proposed. Unlike in previous studies, by incorporating fiber birefringence as one of the model's known error sources, the proposed model directly relates gyro performance to mechanical, geometric, thermal and optical parameters in coiled fibers. The influence of these parameters on the gyro drift was numerically calculated according to the presented model. Measurement results of a quadrupole coil within gyroscopes at 10-3 deg/h accuracy confirmed that the bias and its thermal drift induced by the intrinsic high birefringence and its thermal fluctuation in polarization-maintaining fibers are in the order of 10-3 deg/h and 10-2 deg/h. The results also confirmed that the thermal drift induced by the Shupe effect and the photoelastic effect in single-mode fibers are in the order of 10-4 deg/h and 10-3 deg/h, respectively. The proposed model shows that the highly stress-induced birefringence in polarization-maintaining fibers is a dominant source of error that results in bias and thermal drift in high performance interferometric fiber-optic gyroscopes. The model also comprehensively describes how the errors rise from fiber performance in fiber-optic gyroscopes and explains the non-linear dependence that the gyroscopic error has on fiber birefringence.
-
Key words:
- fiber-optic gyroscope /
- thermal drift /
- fiber birefringence /
- fiber coils
-
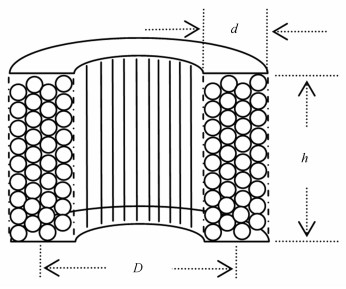
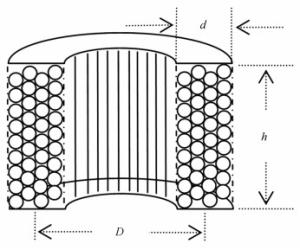
表 1 本文计算所用的光纤及环圈的参数符号及其单位
Table 1. Symbols and units of parameters in fibers and coils used in this calculation
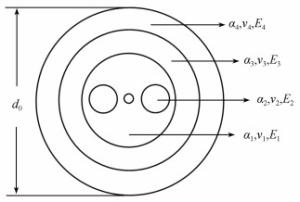
序号 参数 单位 符号 备注 1 自由空间光波长 nm λ 光学参数 2 纤芯折射率 1 n 3 双折射拍长 mm Λ 4 密度 kg/m3 ρ 力学参数 5 泊松比 1 v 6 杨氏模量 Pa E 7 光纤包层直径 μm r 几何参数 8 光纤涂覆外径 μm d0 9 光纤长度 m L 10 环圈直径 mm D 11 环圈厚度 mm d0 12 环圈高度 mm h 13 环圈总层数 1 NL 14 环圈单层匝数 1 NN 15 比热 W/kg·K C 热学参数 16 热导率 W/m·K b 17 热胀系数 /K α 18 辐射热阻 K/W R 19 传导热阻 K/W R′ 20 产生双折射的温度差 K Td 21 纤芯折射率热系数 /K dn/dT 22 双折射热系数 /K H 23 热源功率 W P 表 2 光纤横截面中各区域的组分及符号角标
Table 2. Compositions and symbol subscripts in each area of the fiber cross section
区域 纤芯 包层 应力区 内涂层 外涂层 组分 0.9SiO2 SiO2 0.85SiO2 聚氨酯丙烯酸酯 环氧丙烯酸酯 0.1GeO2 0.15B2O3 角标 0 1 2 3 4 表 3 光纤陀螺所用3种类型保偏光纤的几何参数
Table 3. Geometric parameters of PMFs in FOGs
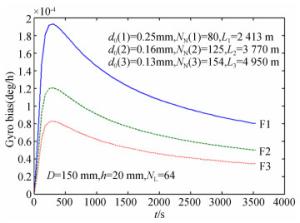
参数/μm 普通保偏 细径保偏 薄涂层细径保偏 包层直径 125 80 80 应力区直径 25 20 20 内涂层直径 180 120 100 外涂层直径 250 170 130 表 4 光纤组分的材料参数值
Table 4. Values of material parameters of fiber components
参数(单位) 纤芯及包层 应力区 内涂层 外涂层 密度/kg·m-3 2 200 2 100 1 000±100 1 300±200 泊松比 0.17 0.188 0.499 47 0.452 杨氏模量/Pa 7.2×1010 6.2×1010 (3±1)×106 1.3×1010 比热/W·kg-1·K-1 740 740 1 600±200 1 600±200 热导率/W·m-1·K-1 1.38 1.38 0.24±0.05 0.21±0.05 热胀系数/1/K 5.6×10-7 1.5×10-6 1.5×10-4 2.1×10-4 表 5 光纤陀螺传感环圈的参数有效值
Table 5. Effective values of parameters of sensing coil in FOGs
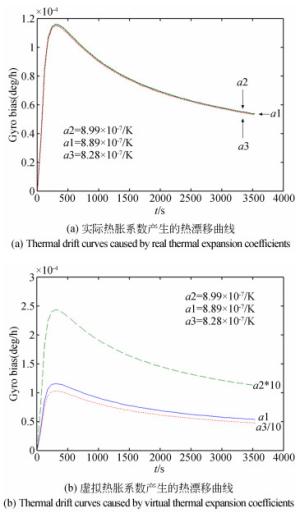
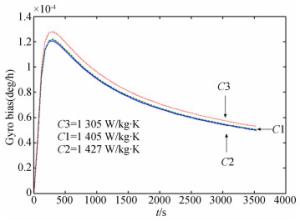
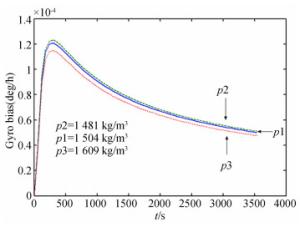
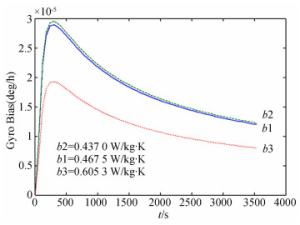
参数(单位) 普通保偏环圈 细径保偏环圈 薄涂层细径保偏环圈 密度/kg·m-3 1 504 1 481 1 609 泊松比 0.21 0.20 0.41 杨氏模量/Pa 2.2×1010 2.5×1010 3.8×1010 比热/W·kg-1·K-1 1 405 1 427 1 305 热导率/W·m-1·K-1 0.467 5 0.437 0 0.605 3 热胀系数/1/K 8.886 4×10-7 8.995 8×10-7 8.282 8×10-7 表 6 高精度干涉式光纤陀螺的传感环圈设计参量
Table 6. Parameters of sensing coil in IFOGs
环圈参量(单位) 固定数值 平均直径/mm 150 总层数 64 单层匝数 125 光纤长度/m 3 770 -
[1] HERVRE C L. The Fiber-Optic Gyroscope[M]. 2nd ed. Boston:Artech House, 2014. [2] PATUREL Y, HONTHAAS J, LEFÈVRE H, et al.. One nautical mile per month FOG-based strapdown inertial navigation system:a dream already within reach?[J]. Gyroscopy and Navigation, 2014, 5(1):1-8. doi: 10.1134/S207510871401009X [3] VALI V, SHORTHILL R W. Fiber ring interferometer[J]. Applied Optics, 1976, 15(5):1099-1100. doi: 10.1364/AO.15.001099 [4] SHUPE D M. Thermally induced nonreciprocity in the fiber-optic interferometer[J]. Applied Optics, 1980, 19(5):654-655. doi: 10.1364/AO.19.000654 [5] FRIGO N J. Compensation of linear sources of non-reciprocity in Sagnac interferometers[J]. Proceedings of SPIE, 1983, 412:268-271. doi: 10.1117/12.935827 [6] LEFÈVRE H C. The fiber-optic gyroscope:challenges to become the ultimate rotation-sensing technology[J]. Optical Fiber Technology, 2013, 19(6):828-832. doi: 10.1016/j.yofte.2013.08.007 [7] KHAN J A, GUDMUNDSDOTTIR L, ALAM M. Fiber optic gyroscope coils:performance characterization[J]. Proceedings of SPIE, 2017, 10208:1020807. doi: 10.1117/12.2261977 [8] MINAKUCHI S, SANADA T, TAKEDA N, et al.. Thermal strain in lightweight composite fiber-optic gyroscope for space application[J]. Journal of Lightwave Technology, 2015, 33(12):2658-2662. doi: 10.1109/JLT.2014.2375198 [9] CHAMOUN J N, DIGONNET M J F. Noise and bias error due to polarization coupling in a fiber optic gyroscope[J]. Journal of Lightwave Technology, 2015, 33(13):2839-2847. doi: 10.1109/JLT.2015.2416155 [10] MOHR F, SCHADT F. Bias error in fiber optic gyroscopes due to elasto-optic interactions in the sensor fiber[J]. Proceedings of SPIE, 2004, 5502:410-413. doi: 10.1117/12.566654 [11] MOHR F, SCHADT F. Rigorous treatment of fiber-environmental interactions in fiber gyroscopes[C]. Proceedings of 2008 IEEE Region 8 International Conference on Computational Technologies in Electrical and Electronics Engineering, IEEE, 2008: 372-375. [12] MOHR F, SCHADT F. Error signal formation in FOGs through thermal and elastooptical environmental influences on the sensing coil[C]. International Sensors and Systems Symposium, Karlsruhe, 2011. [13] OGUT S, OSUNLUK B, OZBAY E. Modeling of thermal sensitivity of a fiber optic gyroscope coil with practical quadrupole winding[C]. Proceedings of SPIE, 2017, 10208: 1020806. [14] TATEDA M, TANAKA S, SUGAWARA Y. Thermal characteristics of phase shift in jacketed optical fibers[J]. Applied Optics, 1980, 19(5):770-773 doi: 10.1364/AO.19.000770 [15] LAGAKOS N, BUCARO J A, JARZYNSKI J. Temperature-induced optical phase shifts in fibers[J]. Applied Optics, 1981, 20(13):2305-2308. doi: 10.1364/AO.20.002305 [16] MUSHA T, KAMIMURA J I, NAKAZAWA M. Optical phase fluctuations thermally induced in a single-mode optical fiber[J]. Applied Optics, 1982, 21(4):694-698. doi: 10.1364/AO.21.000694 [17] WONG D. Thermal stability of intrinsic stress birefringence in optical fibers[J]. Journal of Lightwave Technology, 1990, 8(11):1757-1761. doi: 10.1109/50.60576 [18] CHIANG K S. Temperature sensitivity of coated stress-induced birefringence optical fibers[J]. Optical Engineering, 1997, 36(4):999-1007. doi: 10.1117/1.601293 [19] MCDEARMON G F. Theoretical analysis of the minimization of the temperature sensitivity of a coated optical fiber in a fiber-optic polarimeter[J]. Journal of Lightwave Technology, 1990, 8(1):51-55. doi: 10.1109/50.45929 [20] MOHR F, KIESEL P. Thermal sensitivity of sensing coils for fibre gyroscopes[J]. Proceedings of SPIE, 1984, 514:305-308. doi: 10.1117/12.945103 [21] MOHR F. Thermooptically induced bias drift in fiber optical Sagnac interferometers[J]. Journal of Lightwave Technology, 1996, 14(1):27-41. doi: 10.1109/50.476134 -





 下载:
下载: