-
摘要: 为了研究史密斯-帕塞尔自由电子激光的输出频率和光栅槽深、光栅槽长、光栅槽宽的关系,对于基于矩形光栅的史密斯-帕塞尔自由电子激光利用粒子模拟软件进行模拟和理论分析。首先,利用粒子模拟软件模拟对于基于矩形光栅的史密斯-帕塞尔自由电子激光进行了研究,发现史密斯-帕塞尔自由电子激光的输出频率随光栅槽深、光栅槽长、光栅槽宽的增大而减少。接着,对史密斯-帕塞尔自由电子激光的光栅槽进行了理论分析,发现每个光栅槽都可以等效为一个LC谐振电路,并发现在史密斯-帕塞尔自由电子激光中存在两种辐射,一种是史密斯-帕塞尔辐射,另一种是LC振荡辐射。最后,对光栅槽的LC振荡辐射进行了估算,发现史密斯-帕塞尔自由电子激光输出频率的模拟值与光栅槽的LC振荡辐射估算值的数量级均为102 GHz,且变化规律上一致。据此推测决定史密斯-帕塞尔自由电子激光输出频率的应该是光栅槽,而不是谐振腔。Abstract: In order to study the relationship between the output frequency of Smith-Purcell free-electron laser and the depth, length and width of grating groove, the rectangular grating size of Smith-Purcell free-electron laser is discussed by means of theoretical analysis and particle simulation methods. First, by particle simulation, we found that the output frequency of Smith-Purcell free-electron laser decreases with the increase of grating groove depth, grating groove length and grating groove width. Then, the grating groove of Smith-Purcell free-electron laser is discussed by means of theoretical analysis. It is found that each grating groove can be equivalent to an LC resonant circuit. There are two kinds of radiation in Smith-Purcell free-electron laser, one is Smith-Purcell radiation and the other is LC oscillatory radiation. Finally, the LC oscillatory radiation of grating groove is estimated as well. It is found that the simulated values of output frequency of Smith-Purcell free-electron laser and the estimation values of LC oscillatory radiation of grating groove are both on the order of 102 GHz, and the variation is consistent. It is inferred that the output frequency of Smith-Purcell free-electron laser should be determined by grating groove rather than resonator.
-
Key words:
- physical electronics /
- free-electron laser /
- grating /
- resonator /
- Smith-Purcell radiation /
- LC resonance circuit
-
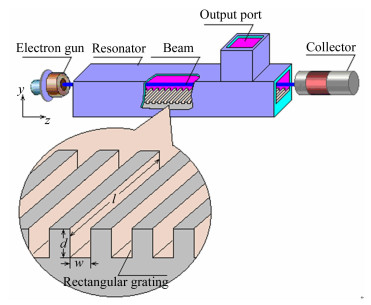
表 1 基于矩形光栅的SP FEL的谐振腔参数和电子束参数
Table 1. Resonator parameters and electron beam parameters of the SP FEL based on rectangular grating
Parameters Value Parameters Value Width of resonator/mm 1.5 Transverse size of beam/mm 0.5 Length of resonator/mm 36.9 Beam voltage/kV 50 Height of resonator/mm 0.75 Current/A 10 表 2 在不同光栅槽深时SP FEL输出频率的模拟值
Table 2. Simulation values of output frequency of SP FEL at different depths of grating groove
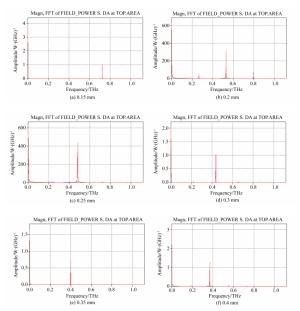
Parameters Values Number of periods 32 Period length of grating/mm 0.3 Slot length of grating/mm 1.5 Slot width of grating/mm 0.1 Slot depth of grating/mm 0.15 0.2 0.25 0.3 0.35 0.4 Simulation value of output frequency / GHz 723.379 529.786 483.632 436.827 400.121 370.060 表 3 在不同光栅槽长时SP FEL输出频率的模拟值
Table 3. Simulation values of output frequency of SP FEL at different lengths of grating groove
Parameters Values Number of periods 32 Period length of grating/mm 0.3 Slot width of grating/mm 0.1 Slot depth of grating/mm 0.2 Slot length of grating/mm 0.75 1.5 Simulation value of output frequency/GHz 727.255 529.786 表 4 在不同光栅槽宽时SP FEL输出频率的模拟值
Table 4. Simulation values of output frequency of SP FEL at different widths of grating groove
Parameters Values Number of periods 32 Period length of grating/mm 0.3 Slot length of grating/mm 1.5 Slot depth of grating/mm 0.2 Slot width of grating/mm 0.1 0.15 0.2 Simulation value of output frequency / GHz 529.786 515.823 508.692 表 5 不同光栅槽深时光栅槽的LCR估算值
Table 5. Estimation values of LCR of grating groove at different groove depths
Slot depth of grating/mm Estimation value of LCR/GHz 0.15 302.849 0.2 224.843 0.25 178.800 0.3 148.412 0.35 126.854 0.4 110.765 表 6 不同光栅槽长时光栅槽的LCR估算值
Table 6. Estimation values of LCR of grating groove at different groove lengths
Slot length of grating/mm Estimation value of LCR/GHz 0.75 317.976 1.5 224.843 表 7 不同光栅槽宽时光栅槽的LCR估算值
Table 7. Estimation values of LCR of grating groove at different groove widths
Slot width of grating/mm Estimation value of LCR/GHz 0.1 224.843 0.15 150.806 0.2 137.482 -
[1] SMITH S J, PURCELL E M. Visible light from localized surface charges moving across a grating[J]. Physical Review, 1953, 92(4):1069. http://cn.bing.com/academic/profile?id=bb7bebc0a23091065c994d7cd063b8df&encoded=0&v=paper_preview&mkt=zh-cn [2] GREEN B, KOVALEV S, ASGEKAR V, et al.. High-field high-repetition-rate sources for the coherent THz control of matter[J]. Scientific Reports, 2016, 6:22256. doi: 10.1038/srep22256 [3] MENG X ZH, WANG M H, ZHANG L M, et al.. Characteristic analysis of a Smith-Purcell terahertz source[J]. Photonics Research, 2016, 4(5):162-167. doi: 10.1364/PRJ.4.000162 [4] 孟现柱, 王明红, 孙桂芳, 等.基于微型谐振腔的史密斯-帕赛尔自由电子激光[J].聊城大学学报(自然科学版), 2018, 31(4):48-51. http://d.old.wanfangdata.com.cn/Periodical/lcsyxb-zrkxb201804009MENG X ZH, WANG M H, SUN G F, et al.. Smith-Purcell free electron laser based on micro-resonator[J]. Journal of Liaocheng University (Natural Science Edition), 2018, 31(4):48-51. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/lcsyxb-zrkxb201804009 [5] 孟现柱, 王明红, 张黎明, 等.基于史密斯——帕赛尔效应的太赫兹振荡器的原理与特性分析[J].光子学报, 2016, 45(4):0423003. http://d.old.wanfangdata.com.cn/Periodical/gzxb201604003MENG X ZH, WANG M H, ZHANG L M, et al.. Principle and characteristics analysis of a terahertz oscillator based on Smith-Purcell effect[J]. Acta Photonica Sinica, 2016, 45(4):0423003. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gzxb201604003 [6] LIU W H, LU Y L, WANG L, et al.. A multimode terahertz-Orotron with the special Smith-Purcell radiation[J]. Applied Physics Letters, 2016, 108(18):183510. doi: 10.1063/1.4949015 [7] LI D, IMASAKI K, YANG Z. Three-dimensional simulation of super-radiant Smith-Purcell radiation[J]. Applied Physics Letters, 2006, 88(20):201501. doi: 10.1063/1.2204750 [8] ZHOU Y C, ZHANG Y X, LIU SH G. Electron-beam-driven enhanced terahertz coherent Smith-Purcell radiation within a cylindrical quasi-optical cavity[J]. IEEE Transactions on Terahertz Science and Technology, 2016, 6(2):262-267. doi: 10.1109/TTHZ.2016.2516524 [9] 史宗君, 唐效频, 兰峰, 等.太赫兹频段一维介质光子晶体中的史密斯-帕塞尔辐射特性模拟[J].红外与毫米波学报, 2014, 33(2):183-187. http://d.old.wanfangdata.com.cn/Periodical/hwyhmb201402013SHI Z J, TANG X P, LAN F, et al.. Simulation of terahertz Smith-Purcell radiation from one-dimensional dielectric photonic crystal[J]. Journal of Infrared and Millimeter Waves, 2014, 33(2):183-187. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hwyhmb201402013 [10] LI W W, XU Y F, LU Y L, et al.. Enhancement of coherent THz Smith-Purcell radiation by resonance overlapping[J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2017, 38(1):12-21. doi: 10.1007/s10762-016-0304-7 [11] KUMAR P, BHASIN L, TRIPATHI V K, et al.. Smith-Purcell terahertz radiation from laser modulated electron beam over a metallic grating[J]. Physics of Plasmas, 2016, 23(9):093301. doi: 10.1063/1.4963004 [12] ZHANG P, ANG L K, GOVER A. Enhancement of coherent Smith-Purcell radiation at terahertz frequency by optimized grating, prebunched beams, and open cavity[J]. Physical Review Special Topics-Accelerators and Beams, 2015, 18(2):020702. doi: 10.1103/PhysRevSTAB.18.020702 [13] ZHANG P, ZHANG Y, TANG M. Enhanced THz Smith-Purcell radiation based on the grating grooves with holes array[J]. Optics Express, 2017, 25(10):10901-10910. doi: 10.1364/OE.25.010901 [14] 刘维浩, 陆亚林, 贾启卡.一种基于特异Smith-Purcell效应的太赫兹辐射源: 中国, CN201610220733.5[P]. 2016-08-03.LIU W H, LU Y L, JIA Q K. Terahertz radiation source based on special Smith-Purcell effect: CN, CN201610220733.5[P]. 2016-08-03. (in Chinese) [15] 刘维浩, 梁林波, 陆亚林, 等.基于两段矩形光栅的史密斯-帕赛尔电磁辐射源: 中国, CN201710347815.0[P]. 2017-05-07.LIU W H, LIANG L B, LU Y L, et al.. Smith passail electromagnetic radiation source based on two rectangular grating: CN, CN201710347815.0[P]. 2017-05-07. (in Chinese) [16] LIANG L B, LIU W H, JIA Q K, et al.. High-harmonic terahertz Smith-Purcell free-electron-laser with two tandem cylindrical-gratings[J]. Optics Express, 2017, 25(3):2960-2968. doi: 10.1364/OE.25.002960 [17] LIU W X, TANG CH X, HUANG W H. Characteristics of terahertz coherent transition radiation generated from picosecond ultrashort electron bunches[J]. Chinese Physics B, 2010, 19(6):062902. doi: 10.1088/1674-1056/19/6/062902 [18] CHEN J Y, ZHENG L, ZHANG Y CH, et al.. A novel Smith-Purcell free electron laser[J]. International Journal of Electronics, 2011, 88(4):467-471. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/00207210010013238 [19] KUMAR P, BHASIN L, TRIPATHI V K, et al.. Smith-Purcell terahertz radiation from laser modulated electron beam over a metallic grating[J]. Physics of Plasmas, 2016, 23(9):093301. doi: 10.1063/1.4963004 [20] ZHANG Y X, DONG L. Enhanced coherent terahertz Smith-Purcell superradiation excited by two electron-beams[J]. Optics Express, 2012, 20(20):22627-22635. doi: 10.1364/OE.20.022627 [21] BEI H, DAI D D, DAI ZH M. Simulation of Smith-Purcell radiation from compact terahertz source[J]. High Power Laser and Particle Beams, 2008, 20(12):2067-2072. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=qjgylzs200812027 [22] GAO X, YANG Z Q, QI L M, et al.. Three-dimensional simulation of a Ka-band relativistic Cherenkov source with metal photonic-band-gap structures[J]. Chinese Physics B, 2009, 18(6):2452-2458. doi: 10.1088/1674-1056/18/6/055 [23] 席阳红, 谢国大, 徐辉, 等.时变磁化等离子体的LTJEC-FDTD方法研究[J].发光学报, 2018, 39(7):1029-1035. http://d.old.wanfangdata.com.cn/Periodical/fgxb201807021XI Y H, XIE G D, XU H, et al.. Analysis of time-varying magnetic plasma by using LTJEC-FDTD method[J]. Chinese Journal of Luminescence, 2018, 39(7):1029-1035. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/fgxb201807021 [24] 李传起, 范庆斌, 陆叶, 等.多信道异质结构光子晶体滤波器[J].光学 精密工程, 2015, 23(8):2171-2177. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201508008LI CH Q, FAN Q B, LU Y, et al.. Multi-channel heterophotonic crystal filter[J]. Opt. Precision Eng., 2015, 23(8):2171-2177. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201508008 [25] 杨波, 梁静秋, 梁中翥, 等.液晶-金属光子晶体波导的光学特性[J].发光学报, 2011, 32(11):1159-1164. http://d.old.wanfangdata.com.cn/Periodical/fgxb201111013YANG B, LIANG J Q, LIANG ZH ZH, et al.. The optical properties of a liquid crystal-metal photonic crystal waveguide[J]. Chinese Journal of Luminescence, 2011, 32(11):1159-1164. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/fgxb201111013 [26] 刘杰, 铁生年, 卢辉东.多信道二维光子晶体滤波器[J].光学 精密工程, 2016, 24(5):1021-1027. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201605009LIU J, TIE SH N, LU H D. Multi-channel drop filter based on two-dimensional photonic crystal[J]. Opt. Precision Eng., 2016, 24(5):1021-1027. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201605009 [27] MENG X ZH. Smith-Purcell free electron laser based on a semi-conical resonator[J]. Optics Communications, 2012, 285(6):975-979. doi: 10.1016/j.optcom.2011.11.100 [28] MENG X ZH. Smith-Purcell free electron laser based on a multilayer metal-dielectric stack[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(17):3162-3164. doi: 10.1016/j.ijleo.2012.09.001 [29] MENG X ZH, WANG M H, REN ZH M. Smith-Purcell free electron laser based on the semi-elliptical resonator[J]. Chinese Physics B, 2011, 20(5):050702. doi: 10.1088/1674-1056/20/5/050702 [30] MENG X ZH, WANG M H, REN ZH M. Smith-Purcell radiation in a grating-resonator composite structure[J]. Journal of Infrared and Millimeter Waves, 2016, 35(1):21-24. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hwyhmb201601005 [31] 王雪飞, 卢振武, 王泰升, 等.超表面上表面等离激元波的光栅衍射行为研究[J].中国光学, 2018, 11(1):60-73. doi: 10.3788/CO.20181101.0060WANG X F, LU ZH W, WANG T SH, et al.. Grating diffractive behavior of surface Plasmon wave on meta-surface[J]. Chinese Optics, 2018, 11(1):60-73. (in Chinese) doi: 10.3788/CO.20181101.0060 [32] 刘镜, 刘娟, 王涌天, 等.亚波长金属光栅的表面等离子体激元共振特性[J].中国光学, 2011, 4(4):363-368. doi: 10.3969/j.issn.2095-1531.2011.04.007LIU J, LIU J, WANG Y T, et al.. Resonant properties of sub-wavelength metallic gratings[J]. Chinese Optics, 2011, 4(4):363-368. (in Chinese) doi: 10.3969/j.issn.2095-1531.2011.04.007 -






 下载:
下载: