Activation effect of complex medium on the optical propagation properties of optical quantum well
-
摘要: 利用传输矩阵法研究复介质对光量子阱光传输特性的激活效应机制，结果表明复介质可有效激活光量子阱的光透射率和内部局域电场。无论组成光量子阱的介质是实介质还是复介质，光量子阱内部均存在局域电场，且局域电场均会产生频率量子化并在透射谱中出现分立的窄透射峰。在介质A中掺入激活性杂质的复介电常数虚部k为正时，光量子阱内部局域电场和分立窄透射峰的透射率均出现衰减现象，且随着k值增大内部局域电场单调衰减越来越明显，但光量子阱不同波长位置的局域电场对k值的响应灵敏度不同，其中光量子阱中心波长处对应的电场对k值响应最灵敏；当复介电常数的虚部k为负值时，光量子阱内部局域电场和分立窄透射峰的透射率均出现增益放大现象，随着负虚部|k|值增大，内部局域电场先增大至极大值随后衰减，但光量子阱不同波长位置的局域电场增益放大的极大值及其对应的|k|值大小不同，其中光量子阱短波方向局域电场对|k|值响应最灵敏，长波方向局域电场对|k|值响应灵敏度最低。研究复介质对光量子阱光传输特性的调制机制，对新型光学滤波器、光学放大器和光学全反射镜的理论研究与实际设计，以及光量子阱光传输特性的内在机制研究等，均具有积极的指导意义。Abstract: By using the transmission matrix, the activation effect of complex medium on the optical propagation properties of optical quantum well has been studied. The result shows that, the light transmissivity and internal local electric field of an optical quantum well can be activated by complex medium. There is always an internal local electric field in the optical quantum well made of whether real medium or complex medium. The local electric field will always cause the frequency quantization and the appearance of discrete narrow transmission peaks in the transmission spectrum. Active impurities are added to the medium A. When the imaginary part of dielectric constant of complex medium, namely k, is positive, both the local electric field in the optical quantum well and the transmissivity of discrete narrow transmission peaks will be attenuated. With the increase of k value, the monotonic attenuation of internal local electric field becomes more obvious. However, the sensitivity of the response of local electric field to the positive imaginary part k is different at different wavelengths of optical quantum well, and the electric field at the central wavelength of the quantum well is the most sensitive to the k value. When the imaginary part of dielectric constant of complex medium, is negative, both the local electric field in the optical quantum well and the transmissivity of discrete narrow transmission peaks will have an amplified gain. As the value of negative imaginary part |k| increases, the internal local electric field will increase to a maximal value and then become attenuated. However, the maximal value of the local electric field in gain amplification and the corresponding |k| value are different at different wavelengths of the quantum well. To be specific, the local electric field in the short-wave direction of the quantum well is the most sensitive to |k| value, while the local electric field in the long-wave direction is the least sensitive to |k| value. The modulation mechanism of complex medium towards the light transmission characteristics of optical quantum well has positive guiding significance for the theoretical research and practical design of new optical filters, optical amplifiers and optical holophotes, and for the research of internal mechanism of light transmission characteristics of an optical quantum well.
-
图 2 一维光子晶体的带隙结构。(a)(ABA)10; (b)(AB)5(BA)5
Figure 2. Band-gap structure of 1D photonic crystals.(a)(ABA)10; (b)(AB)5(BA)5
图 4 (AB)3(ABA)4(BA)3的透射谱与电场分布
Figure 4. Transmission spectrum and electric field distributions of PQW(AB)3(ABA)4(BA)3
图 5 εA=6.670+0.1i时(AB)3(ABA)4(BA)3的透射谱与电场分布
Figure 5. Transmission spectrum and electric field distributions of PQW(AB)3(ABA)4(BA)3 with εA of 6.670+0.1i
图 6 εA=6.670-0.02i时(AB)3(ABA)4(BA)3的透射谱与电场分布
Figure 6. Transmission spectrum and electric field distributions of PQW(AB)3(ABA)4(BA)3 with εA of 6.670-0.02i
图 7 εA=6.670+ki时, k对(AB)3(ABA)4(BA)3内部电场的影响
Figure 7. Electric field distributions versus k of PQW(AB)3(ABA)4(BA)3 with εA of 6.670+ki
-
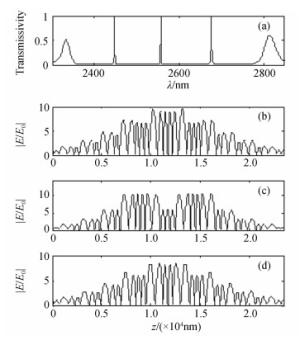
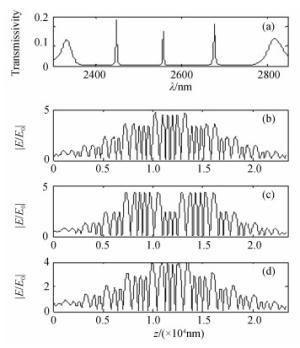
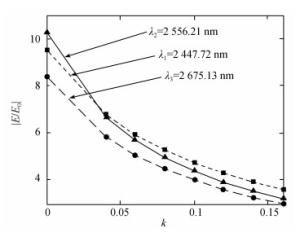
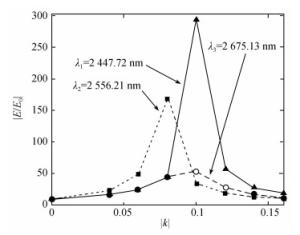
[1] YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Physical Review Letters, 1987, 58(20):2059-2062. doi: 10.1103/PhysRevLett.58.2059 [2] JOHN S. Strong localization of photons in certain disordered dielectric superlattices[J]. Physical Review Letters, 1987, 58(23):2486-2489. doi: 10.1103/PhysRevLett.58.2486 [3] 张峰, 张海鹍, 陈涛, 等.掺钕双包层大模场保偏光子晶体光纤激光器[J].中国激光, 2017, 44(2):0201020. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201702021ZHANG F, ZHANG H K, CHEN T, et al.. Nd-doped double-clad large-mode-area polarization-maintaining photonic crystal fiber laser[J]. Chinese Journal of Lasers, 2017, 44(2):0201020. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201702021 [4] 陈颖, 曹会莹, 韩帅涛, 等.含吸收介质的光子晶体法布里-珀罗异质结构的传感特性研究[J].光学学报, 2017, 37(2):0223003.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201702029(in Chinese) CHEN Y, CAO H Y, HAN SH T, et al.. Sensing property of photonic crystal fabry-pérot heterogeneous structure with absorption medium[J]. Acta Optica Sinica, 2017, 37(2):0223003. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201702029 [5] 李天琦, 毛小洁, 雷健, 等.固体激光器与光纤激光器对光子晶体光纤棒耦合的分析与对比[J].中国光学, 2018, 11(6):958-973. doi: 10.3788/CO.20181106.0958LI T Q, MAO X J, LEI J, et al.. Analysis and comparison of solid-state lasers and fiber lasers on the coupling of rod-type photonic crystal fiber[J]. Chinese Optics, 2018, 11(6):958-973. (in Chinese) doi: 10.3788/CO.20181106.0958 [6] 张琪, 张红, 周强, 等.灭多威分子印迹光子晶体传感器的制备及应用[J].分析化学, 2019, 47(6):883-889. http://d.old.wanfangdata.com.cn/Periodical/fxhx201906012ZHANG Q, ZHANG H, ZHOU Q, et al..Preparation and application of methomyl molecularly imprinted photonic crystal sensor[J]. Chinese Journal of Analytical Chemistry, 2019, 47(6):883-889.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/fxhx201906012 [7] 王一飞, 周丽君, 杨吉, 等.光子晶体纤维素膜检测二氧化硫气体[J].分析化学, 2018, 46(9):1472-1478. http://d.old.wanfangdata.com.cn/Periodical/fxhx201809019WANG Y F, ZHOU L J, YANG J, et al..Detection of sulfur dioxide using cellulose photonic crystal membrane[J]. Chinese Journal of Analytical Chemistry, 2018, 46(9):1472-1478.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/fxhx201809019 [8] 海一娜, 邹永刚, 田锟, 等.水平腔面发射半导体激光器研究进展[J].中国光学, 2017, 10(2):194-206. doi: 10.3788/CO.20171002.0194HAI Y N, ZOU Y G, TIAN K, et al.. Research progress of horizontal cavity surface emitting semiconductor lasers[J]. Chinese Optics, 2017, 10(2):194-206. (in Chinese) doi: 10.3788/CO.20171002.0194 [9] 刘继平, 李海波, 孟祥东, 等.含点缺陷二维函数光子晶体的本征场分布[J].中国激光, 2018, 5(8):0803001. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201808017LIU J P, LI H B, MENG X D, et al.. Eigenfield distribution of two-dimensional functional photonic crystals with point defects[J]. Chinese Journal of Lasers, 2018, 45(8):0803001. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201808017 [10] 杜木青, 张伶莉, 刘永军.液晶及其不同填充结构对光子晶体光纤传输特性的影响[J].液晶与显示, 2018, 33(2):116-122. http://d.old.wanfangdata.com.cn/Periodical/yjyxs201802003DU M Q, ZHANG L L, LIU Y J. Effect of liquid crystal and its different filling structure on the transmission properties of photonic crystal fiber[J]. Chinese Journal of Liquid Crystals and Displays, 2018, 33(2):116-122.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yjyxs201802003 [11] 马季, 吴向尧, 刘晓静, 等.光子晶体缺陷层吸收特性的研究[J].中国激光, 2014, 41(3):0306002. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201403025MA J, WU X Y, LIU X J, et al.. Research on the absorption property of defect layer in photon crystals[J]. Chinese Journal of Lasers, 2014, 41(3):0306002. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201403025 [12] 孟宪芹, 王维, 谭纪风, 等.光子晶体滤色实现五基色显示[J].液晶与显示, 2019, 34(6):576-581. http://d.old.wanfangdata.com.cn/Periodical/yjyxs201906007MENG X Q, WANG W, TAN J F, et al..Application of photonic crystals for colorful display[J]. Chinese Journal of Liquid Crystals and Displays, 2019, 34(6):576-581.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yjyxs201906007 [13] 苏安, 王高峰, 蒙成举, 等.光子晶体二元缺陷微腔的光传输特性[J].红外与激光工程, 2017, 46(6):0620004. http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201706020SU A, WANG G F, MENG CH J, et al.. Light propagation characteristic of dual defect microcavity of photonic crystal[J]. Infrared and Laser Engineering, 2017, 46(6):0620004. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201706020 [14] 苏安, 蒙成举, 高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制[J].中国激光, 2014, 41(3):0306001. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201403024SU A, MENG CH J, GAO Y J. Modulation of activated impurity on filter property of photonic crystal quantum well[J]. Chinese Journal of Lasers, 2014, 41(3):0306001. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201403024 [15] 苏安, 蒙成举, 高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器[J].中国激光, 2013, 40(10):01006001. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201310028SU A, MENG CH J, GAO Y J. Filter with one-dimensional photonic crystal quantum well possessing high-quality filtering functions[J]. Chinese Journal of Lasers, 2013, 40(10):01006001. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg201310028 [16] 苏安, 高英俊.双重势垒一维光子晶体量子阱的光传输特性研究[J].物理学报, 2012, 61(23):234208. http://d.old.wanfangdata.com.cn/Periodical/wlxb201223036SU A, GAO Y J. Light propagation characteristics of one-dimensional photonic crystal with double-barrier quantum well[J]. Acta Physica Sinica, 2012, 61(23):234208. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/wlxb201223036 [17] 康永强, 高鹏, 刘红梅, 等.单负材料组成一维光子晶体双量子阱结构的共振模[J].物理学报, 2015, 64(6):064207. http://d.old.wanfangdata.com.cn/Periodical/wlxb201506020KANG Y Q, GAO P, LIU H M, et al.. Resonant modes in photonic double quantum well structures with single-negative materials[J]. Acta Physica Sinica, 2015, 64(6):064207. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/wlxb201506020 [18] 熊翠秀, 邓杨保, 邓曙光.基于对称嵌套式光子晶体量子阱的多通道滤波器[J].激光与光电子学进展, 2016, 53(4):041601. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgygdzxjz201604026XIONG C X, DENG Y B, DENG SH G. Multi-channel filter based on symmetric nested photonic crystals quantum well[J]. Laser & Optoelectronics Progress, 2016, 53(4):041601. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgygdzxjz201604026 [19] 钟远聪.光子晶体缺陷中掺入增益介质的小信号增益特性[J].人工晶体学报, 2014, 43(6):1583-1587. http://d.old.wanfangdata.com.cn/Periodical/rgjtxb98201406049ZHONG Y C. Small signal gain characteristics of the defect photonic crystals with gain medium[J]. Journal of Synthetic Crystals, 2014, 43(6):1583-1587. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/rgjtxb98201406049 [20] 娄淑琴, 王智, 任国斌, 等.具有复介电常量二维光子晶体的特性研究[J].光学学报, 2004, 24(3):313-318. http://d.old.wanfangdata.com.cn/Periodical/gxxb200403006LOU SH Q, WANG ZH, REN G B, et al.. The research on the properties of two-dimensional photonic crystal with the imaginary part of dielectric constant[J]. Acta Optica Sinica, 2004, 24(3):313-318. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxxb200403006 -
下载:
图(8)
计量
- 文章访问数: 1834
- HTML全文浏览量: 881
- PDF下载量: 43
- 被引次数: 0
