大孔径静态干涉成像光谱仪径向畸变导致的谱线偏移误差的校正

安玲坪; 王爽; 张耿; 李娟; 刘学斌

doi:10.37188/CO.2020-0084

大孔径静态干涉成像光谱仪径向畸变导致的谱线偏移误差的校正

doi: 10.37188/CO.2020-0084

安玲坪^{1, 2,},
王爽^1, ,,
张耿¹,
李娟¹,
刘学斌¹

1.
中国科学院西安光学精密机械研究所光谱成像技术重点实验室，陕西西安 710119
2.
中国科学院大学北京 100049

基金项目: 国家重点研发计划项目（No. 2018YFB0504900，No. 2018YFB0504901）

详细信息

作者简介:
安玲坪(1996—)，女，山西忻州人，博士研究生，2018年于太原理工大学获得学士学位，主要从事光谱成像仪器定量化技术研究。E-mail：anlingping@opt.cn

王爽：王　爽(1980—)，男，黑龙江东宁人，博士，研究员，硕士生导师，2002年、2006年于北京理工大学分别获得学士、硕士学位，2014年于中国科学院西安光学精密机械研究所获得博士学位，主要从事光谱成像理论与仪器开发、光谱成像数据处理与定量化研究。E-mail：wangshuang@opt.ac.cn

中图分类号: TP751.1
计量
- 文章访问数: 263
- HTML全文浏览量: 98
- PDF下载量: 31
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-08
- 修回日期: 2020-06-15
- 网络出版日期: 2021-02-08
- 刊出日期: 2021-04-01

Corrective method for spectral offset error caused by radial distortion in the large aperture static imaging spectrometer

AN Ling-ping^{1, 2
,},
WANG Shuang^{1
, ,},
ZHANG Geng¹,
LI Juan¹,
LIU Xue-bin¹

1.
Key Laboratory of Spectral Imaging Technology, Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: Supported by National Key R&D Program of China (No. 2018YFB0504900, No. 2018YFB0504901)

More Information

Corresponding author: wangshuang@opt.ac.cn

摘要

摘要: 为提高大孔径静态干涉成像光谱仪在视场增大时的光谱定标精度，减小径向畸变对光谱精度的影响，本文提出一种基于光谱——畸变关联模型的光谱定标系数修正方法，给出了波数和波长修正公式。采用594.1 nm和632.8 nm气体激光器对成像光谱仪进行了光谱成像实验，并对数据进行了处理和分析。结果表明，当存在0.3%的桶形畸变时，边缘视场的反演光谱存在2 nm左右的偏移，利用本文方法校正后，谱线偏移减小到0.1 nm左右。该方法仅需根据镜头畸变参数即可完成修正，简化了实验室光谱定标流程，提高了工作效率，也可应用于星载干涉光谱数据的在轨参数校正。
- 大孔径静态干涉成像光谱仪 /
- 光谱定标 /
- 误差校正 /
- 畸变模拟
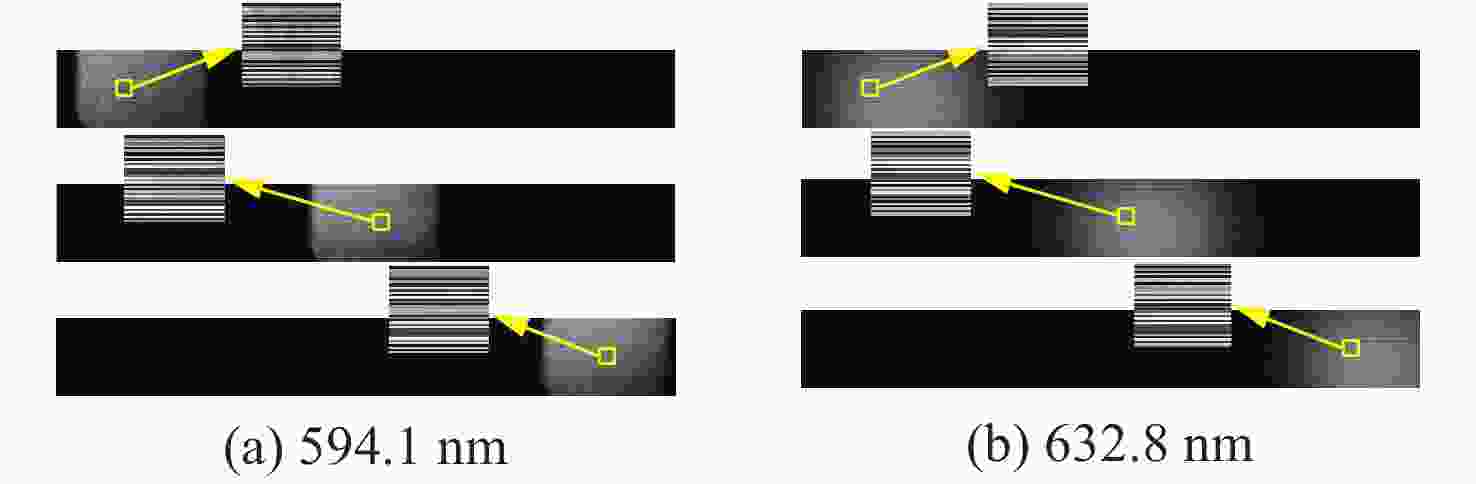
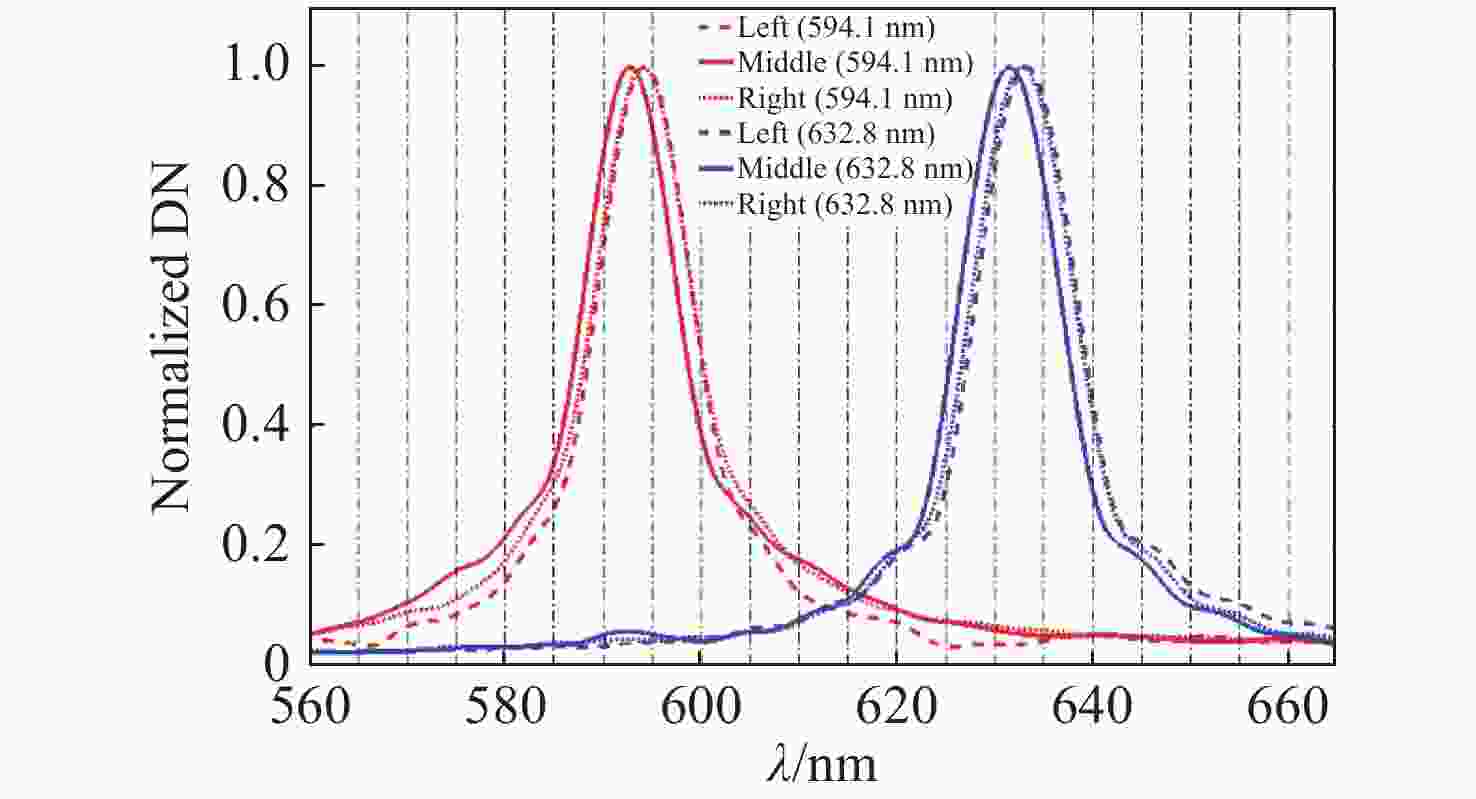
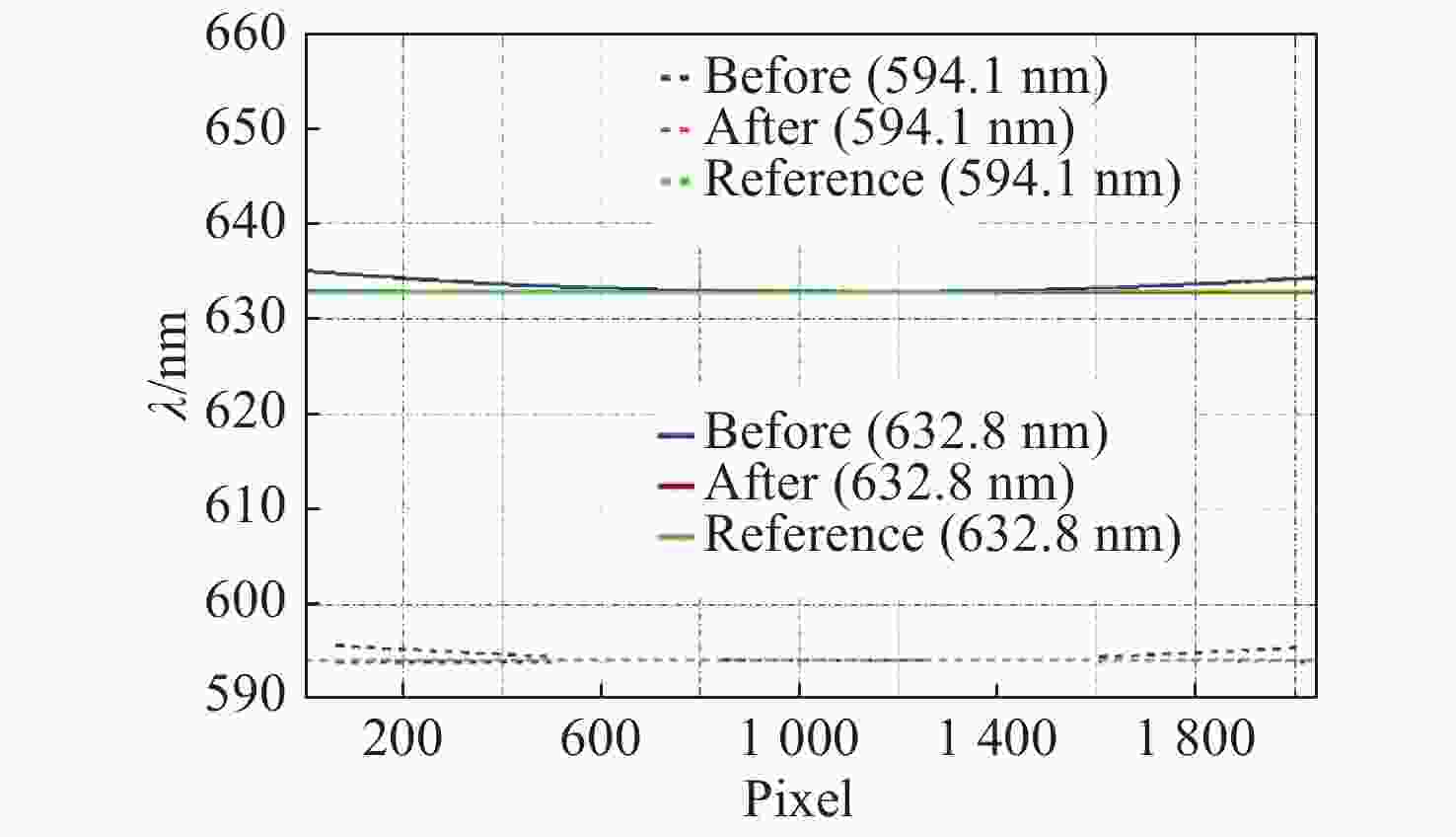
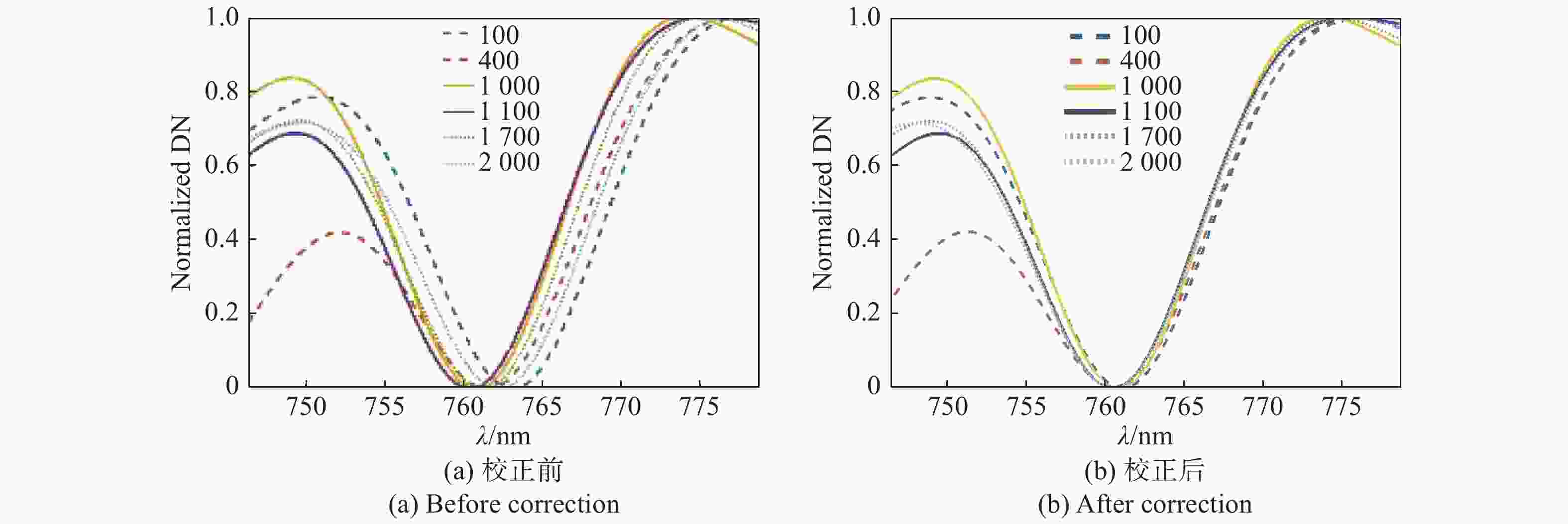
Abstract: In order to improve the spectral calibration accuracy of the large aperture static imaging spectrometer when its field of view is increased, and to reduce the influence of radial distortion on its spectral accuracy, we propose a corrective method for spectral calibration coefficients based on a spectral distortion correlation model. To begin the process, the wave number and wavelength correction formulas are given. Using 594.1 nm and 632.8 nm gas lasers, a spectroscopic imaging experiment was performed on the imaging spectrometer, and the data was processed and analyzed. The results show that when there is a barrel distortion of 0.3%, the inversion spectrum at the edge of the field of view shifts approximately 2 nm. After implementing the corrective method of this paper, the line shift is reduced to approximately 0.1 nm. This method only needs to be corrected according to the lens distortion parameters, which simplifies the laboratory spectral calibration process and improves work efficiency. It can also be applied to the orbit parameter correction of spaceborne interference spectral data.
- Large Aperture Static Imaging Spectrometer (LASIS) /
- spectral calibration /
- error correction /
- distortion simulation

HTML全文

图 1 LASIS结构示意图

Figure 1. Schematic diagram of LASIS structure

下载: 全尺寸图片幻灯片

图 2 LASIS干涉原理示意图

Figure 2. Schematic diagram of LASIS interference

下载: 全尺寸图片幻灯片

图 3 径向畸变效果图

Figure 3. Diagram of the radial distortion effects

下载: 全尺寸图片幻灯片

图 4 仿真试验流程图

Figure 4. Flow chart of the simulation experiment

下载: 全尺寸图片幻灯片

图 5 Matlab模拟结果

Figure 5. Matlab simulation results

下载: 全尺寸图片幻灯片

图 6 光谱定标实验示意图

Figure 6. Schematic diagram of the spectral calibration experiment

下载: 全尺寸图片幻灯片

图 7 激光干涉图

Figure 7. Interferogram of the lasers

下载: 全尺寸图片幻灯片

图 8 激光三视场归一化反演光谱

Figure 8. The normalized inversion spectra of the three fields of view of the lasers

下载: 全尺寸图片幻灯片

图 9 光谱定标误差校正

Figure 9. Correction of spectral calibration

下载: 全尺寸图片幻灯片

图 10 氧气红外吸收带

Figure 10. Absorption band of oxygen in infrared wavelengths

下载: 全尺寸图片幻灯片

表 1 激光中心波长对比

Table 1. Comparison of the lasers’ center wavelength

像元	中心波长/nm
像元	参考值$ {\lambda }_{0} $	校正前$ \lambda $	误差$ \left\|\lambda -{\lambda }_{0}\right\| $	校正后$ \lambda {'} $	误差$ \left\|\lambda {'}-{\lambda }_{0}\right\| $
100	594.1	595.5762	1.4762	594.0097	0.0903
400		594.7603	0.6603	594.0126	0.0874
1000		594.1342	0.0342	594.1260	0.0260
1100		594.1342	0.0342	594.1328	0.0328
1700		594.7186	0.6186	594.0594	0.0406
2000		595.4506	1.3506	594.0136	0.0864
100	632.8	634.5429	1.7429	632.8221	0.0221
400		633.5693	0.7693	632.7368	0.0632
1000		632.8351	0.0351	632.8221	0.0221
1100		632.8114	0.0114	632.8110	0.0110
1700		633.3796	0.5796	632.7107	0.0893
2000		634.1151	1.3151	632.6337	0.1663

下载: 导出CSV

参考文献(20)

[1]	刘红婕, 王凤蕊, 耿峰, 等. 荧光成像技术无损探测光学元件亚表面缺陷[J]. 光学精密工程,2020,28(1):50-59. doi: 10.3788/OPE.20202801.0050 LIU H J, WANG F R, GENG F, et al. Nondestructive detection of optics subsurface defects by fluorescence image technique[J]. Optics and Precision Engineering, 2020, 28(1): 50-59. (in Chinese) doi: 10.3788/OPE.20202801.0050
[2]	何志平, 李春来, 吕刚, 等. 月球表面原位光谱探测技术研究与应用(特约)[J]. 红外与激光工程, 2020, 49(5): 62-69. HE ZH P, LI CH L, LÜ G, et al.. Research and applications of In-Situ lunar surface spectral detection technology(Invited)[J]. Infrared and Laser Engineering, 2020, 49(5): 62-69. (in Chinese)
[3]	郑光辉, 焦彩霞, 上官晨曦, 等. 基于成像光谱技术的土壤剖面发生层划分初探[J]. 光谱学与光谱分析,2019,39(3):882-885. ZHENG G H, JIAO C X, SHANGGUAN CH X, et al. Horizon classification in soil profile using imaging spectroscopy[J]. Spectroscopy and Spectral Analysis, 2019, 39(3): 882-885. (in Chinese)
[4]	朱梦远, 杨红兵, 李志伟. 高光谱图像和叶绿素含量的水稻纹枯病早期检测识别[J]. 光谱学与光谱分析,2019,39(6):1898-1904. ZHU M Y, YANG H B, LI ZH W. Early detection and identification of rice sheath blight disease based on hyperspectral image and chlorophyll content[J]. Spectroscopy and Spectral Analysis, 2019, 39(6): 1898-1904. (in Chinese)
[5]	谭翠媚, 许廷发, 马旭, 等. 图-谱结合的压缩感知高光谱视频图像复原[J]. 中国光学,2018,11(6):949-957. doi: 10.3788/co.20181106.0949 TAN C M, XU T F, MA X, et al. Graph-spectral hyperspectral video restoration based on compressive sensing[J]. Chinese Optics, 2018, 11(6): 949-957. (in Chinese) doi: 10.3788/co.20181106.0949
[6]	MAILHES C, VERMANDE P, CASTANIE F. Spectral image compression[J]. Journal of Optics, 1990, 21(3): 121-132. doi: 10.1088/0150-536X/21/3/006
[7]	LUCEY P G, HORTON K A, WILLIAMS T J, et al. SMIFTS: a cryogenically cooled, spatially modulated imaging infrared interferometer spectrometer[J]. Proceedings of SPIE, 1993, 1937: 130-141. doi: 10.1117/12.157050
[8]	相里斌, 赵葆常, 薛鸣球. 空间调制干涉成像光谱技术[J]. 光学学报,1998,18(1):18-22. doi: 10.3321/j.issn:0253-2239.1998.01.004 XIANG L B, ZHAO B CH, XUE M Q. Spatially modulated imaging interferometry[J]. Acta Optica Sinica, 1998, 18(1): 18-22. (in Chinese) doi: 10.3321/j.issn:0253-2239.1998.01.004
[9]	高泽东, 郝群, 刘宇, 等. 高光谱成像与应用技术发展[J]. 计测技术,2019,39(4):24-34. GAO Z D, HAO Q, LIU Y, et al. Hyperspectral imaging and application technology development[J]. Metrology &Measurement Technology, 2019, 39(4): 24-34. (in Chinese)
[10]	吕群波, 相里斌, 姚涛, 等. 光学畸变对大孔径静态干涉成像光谱仪影响的建模与仿真[J]. 光谱学与光谱分析,2010,30(1):142-145. doi: 10.3964/j.issn.1000-0593(2010)01-0142-04 LÜ Q B, XIANG L B, YAO T, et al. Modeling and simulation of effect of optical distortion on the large aperture static imaging spectrometer[J]. Spectroscopy and Spectral Analysis, 2010, 30(1): 142-145. (in Chinese) doi: 10.3964/j.issn.1000-0593(2010)01-0142-04
[11]	郑玉权. 超光谱成像仪的精细光谱定标[J]. 光学精密工程,2010,18(11):2347-2354. ZHENG Y Q. Precise spectral calibration for hyperspectral imager[J]. Optics and Precision Engineering, 2010, 18(11): 2347-2354. (in Chinese)
[12]	郑子鹏, 邱波, 魏诗雅, 等. 曲线距离法的二维光纤光谱弯曲校正[J]. 光谱学与光谱分析,2019,39(10):3051-3055. ZHENG Z P, QIU B, WEI SH Y, et al. Two-dimensional fiber spectral bending correction based on curve distance method[J]. Spectroscopy and Spectral Analysis, 2019, 39(10): 3051-3055. (in Chinese)
[13]	于丙文, 金伟, 金钦汉, 等. 基于能量重分配的波长偏移校正方法[J]. 高等学校化学学报,2019,40(8):1600-1605. doi: 10.7503/cjcu20190144 YU B W, JIN W, JIN Q H, et al. Wavelength drift correction method based on energy redistribution[J]. Chemical Journal of Chinese Universities, 2019, 40(8): 1600-1605. (in Chinese) doi: 10.7503/cjcu20190144
[14]	朱丹彤, 沈宏海, 杨名宇, 等. 编码孔径成像光谱仪中编码元形变的分析校正[J]. 激光与光电子学进展,2018,55(6):061201. ZHU D T, SHEN H H, YANG M Y, et al. Analysis and correction of coded pixel distortion in coded aperture imaging spectrometer[J]. Laser &Optoelectronics Progress, 2018, 55(6): 061201. (in Chinese)
[15]	董瑛, 相里斌, 赵葆常. 大孔径静态干涉成像光谱仪的干涉系统分析[J]. 光学学报,2001,21(3):330-334. doi: 10.3321/j.issn:0253-2239.2001.03.017 DONG Y, XIANG L B, ZHAO B CH. Analysis of interferometer systerm in a large aperture static imaging spectrometer[J]. Acta Optica Sinica, 2001, 21(3): 330-334. (in Chinese) doi: 10.3321/j.issn:0253-2239.2001.03.017
[16]	董瑛, 相里斌, 赵葆常. 大孔径静态干涉成象光谱仪中的横向剪切干涉仪[J]. 光子学报,1999,28(11):991-995. DONG Y, XIANG L B, ZHAO B CH. Lateral shearing interferometer in large aperture static imaging spectrometer[J]. Acta Photonica Sinica, 1999, 28(11): 991-995. (in Chinese)
[17]	王爽. 大孔径静态干涉光谱成像仪信噪比研究[D]. 西安: 中国科学院研究生院(西安光学精密机械研究所), 2013. WANG SH. Research on the signal-to-noise ratio of large aperture static imaging spectrometer[D]. Xi’an: Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, 2013. (in Chinese).
[18]	SUN Q CH, HOU Y Q, CHEN J. Lens distortion correction for improving measurement accuracy of digital image correlation[J]. Optik, 2015, 126(21): 3153-3157. doi: 10.1016/j.ijleo.2015.07.068
[19]	邹曜璞. 星载傅里叶光谱仪星上数据处理研究[D]. 上海: 中国科学院研究生院(上海技术物理研究所), 2016. ZOU Y P. Research of on-board data processing techniques for Fourier transform spectrometer[D]. Shanghai: Shanghai Institute of Technical Physics of the Chinese Academy of Sciences, 2016. (in Chinese).
[20]	蔡萍, 李潇雁, 唐玉俊, 等. 改进的空间大口径追踪相机畸变校正[J]. 光学精密工程,2019,27(10):2272-2279. doi: 10.3788/OPE.20192710.2272 CAI P, LI X Y, TANG Y J, et al. Improved distortion correction method for spacial large aperture tracking cameras[J]. Optics and Precision Engineering, 2019, 27(10): 2272-2279. (in Chinese) doi: 10.3788/OPE.20192710.2272