-
摘要: 时间延迟干涉技术（Time-delay Interferometry，TDI）对中国引力波探测项目及其它天基激光精密测量任务具有重要的参考价值。在天基引力波探测任务中，需利用激光干涉仪对无拖曳检验质量块间实现十皮米量级的位移测量精度。其中，激光源频率噪声和时钟频率噪声是两项主要噪声。在欧洲主导的LISA（Laser Interferometer Space Antenna）引力波探测项目中，利用TDI对三星上的十二组相位测量值进行延迟和线性组合，构造出臂长相等的干涉仪，从而消除了激光源噪声以及光学平台位移噪声。为了消除时钟噪声，将时钟信号倍频到GHz，再通过相位调制的方式加载到星间激光链路上，最终从时钟边带拍频信号中提取出时钟噪声，并在TDI的数据组合中将时钟噪声项消除。为了实现TDI的时间延迟处理，要求对星间绝对距离进行精确测量。因此，在TDI机制中，星间激光链路需要同时实现位移测量、时钟边带调制和绝对距离测量3个功能。其中，后两个功能分别大约消耗10%和1%的载波激光功率。LISA项目针对TDI技术的地面论证结果表明，TDI技术对激光源和时钟的噪声抑制分别达到了109和5.8×104倍。Abstract: The Time-delay Interferometry (TDI) technique is of important value for China’s gravitational wave detection program and other space-based laser interferometry missions. In space-based gravitational wave detection, laser interferometry is utilized to achieve ten-picometer precision in the displacement measurements between drag-free proof masses. Laser frequency noise and clock frequency noise are the two dominant noises in the measurement. In the European LISA (Laser Interferometer Space Antenna) program for gravitational wave detection, TDI technique is used to remove laser noise and displacement noise of optical platform by time-delaying and linearly combining the twelve phase measurement data of the three satellites and thus creating an interferometer with equal-length beams. For the cancellation of clock noise, the frequencies of onboard clocks are multiplied to GHz levels and then the GHz clock signals are added on inter-satellite laser links by phase modulation. Finally, the clock noise can be extracted from the generated clock-sideband beat note, eliminating the clock noise terms in the TDI data combination. For the time-delay operation in the data post-processing of the TDI, there is also a requirement for the precise measurement of the absolute distances between three satellites. Therefore, in the TDI scheme, there are three functions applicable to the inter-satellite laser links: displacement measurement, clock sideband modulation and absolute distance ranging. The latter two functions consume the power of the optical carrier by 10% and 1%, respectively. The TDI demonstration in the LISA’s ground-based testbed shows the laser noise and clock noise can be suppressed by the factor of 109 and 5.8×104, respectively.
-
图 5 当星座旋转时，
${L'_i} \ne {L_i}$ Figure 5. In the case of the constellation rotation,
${L'_i} \ne {L_i}$ 
图 6 时钟边带调制示意图。EOM：电光调制器
Figure 6. Schematic diagram of clock sideband modulation. EOM: Electro-Optic Modulator
图 7 探测端信号处理示意图。NCO：数控振荡器
Figure 7. Signal processing illustration of photon detection. NCO: Numerically Controlled Oscillator
图 8 在载波相位上调制数据码和伪随机码用于星间数据传输和绝对距离测量示意图
Figure 8. The phase of the carrier is modulated by data codes and pseudo-random codes for the inter-satellite data transmission and absolute distance measurement
-
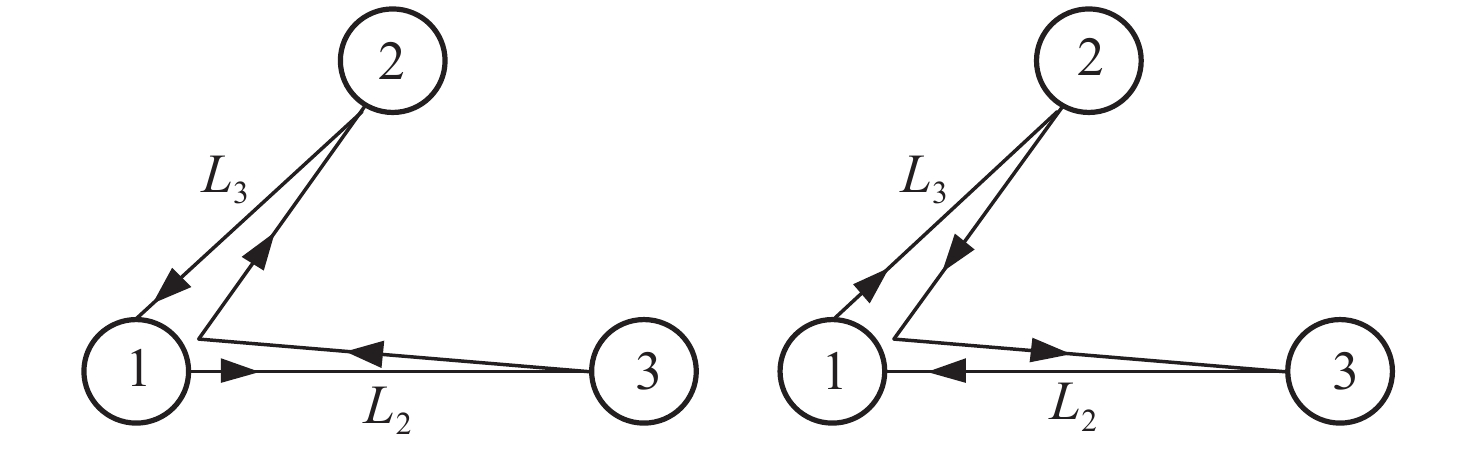
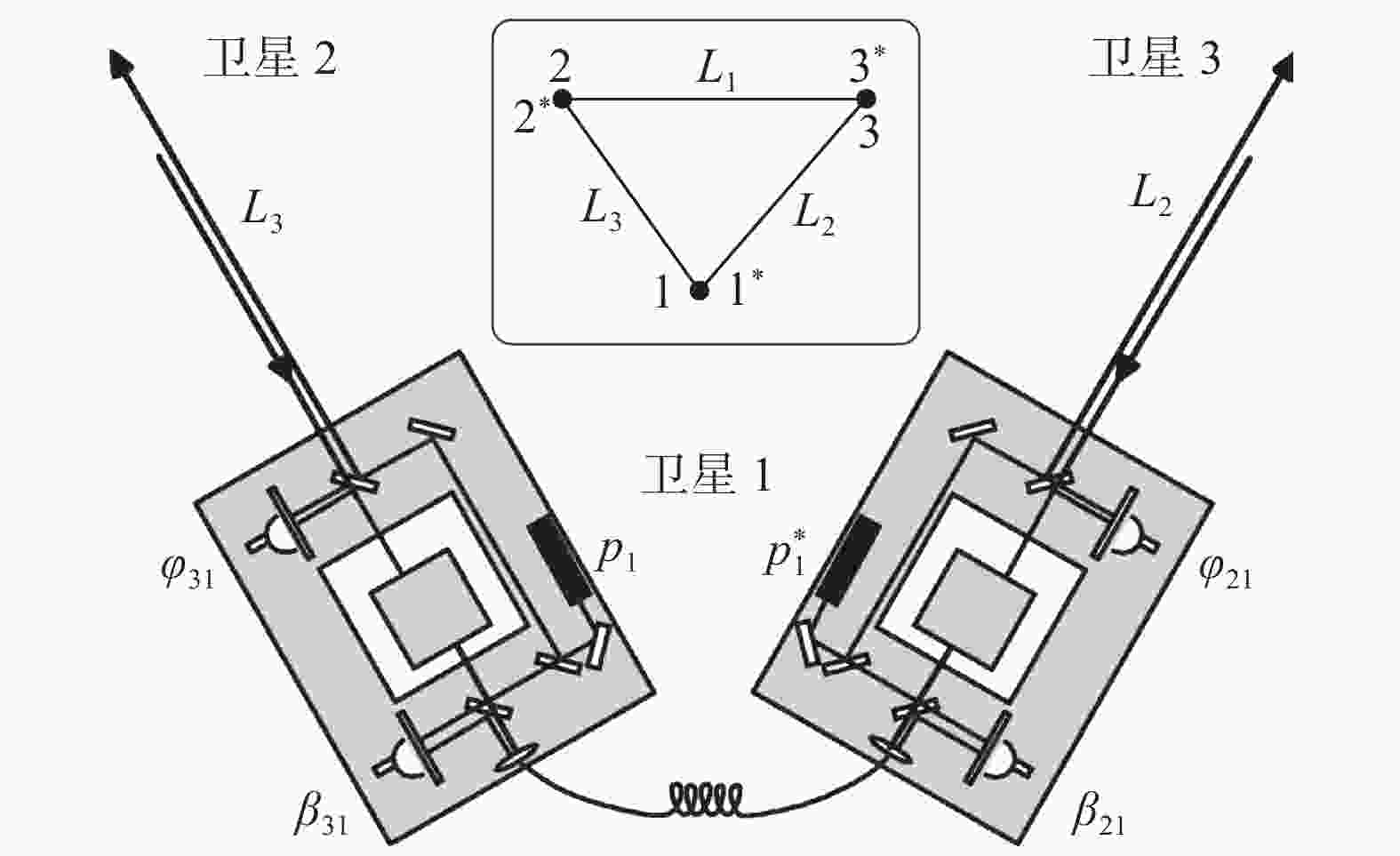
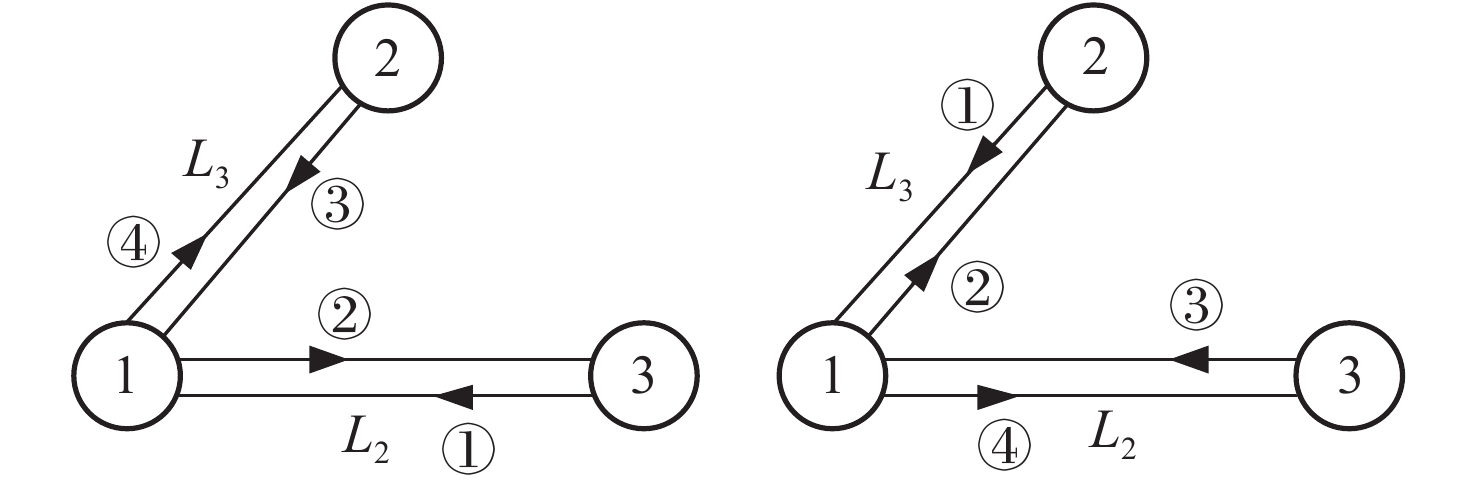
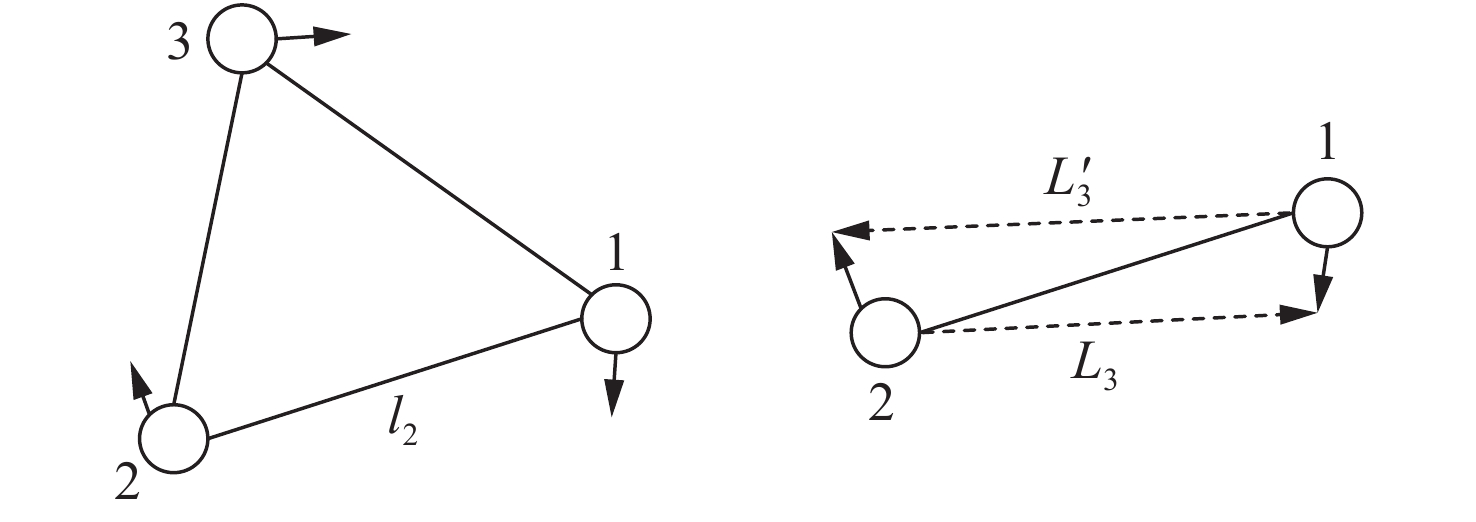
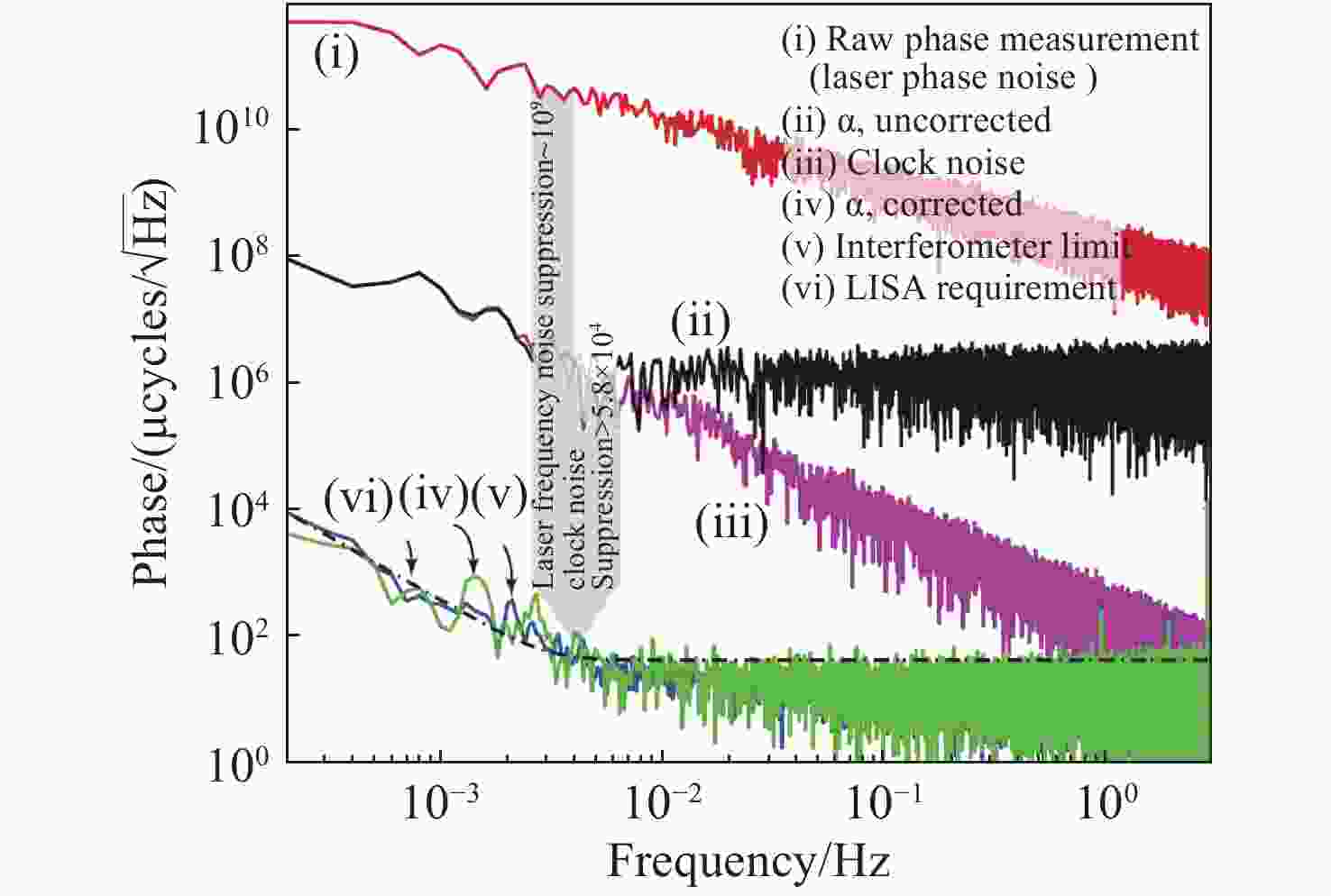
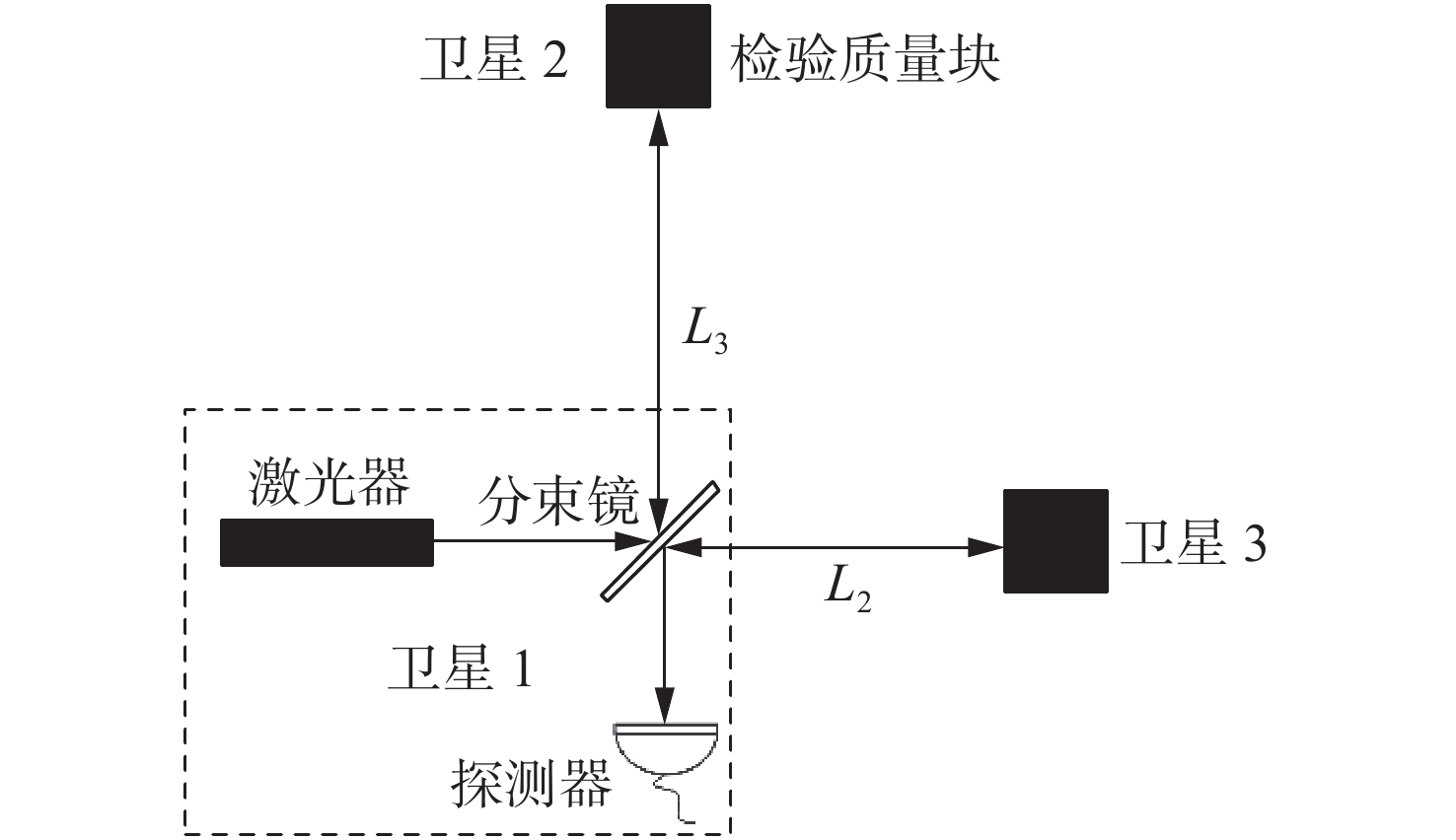
[1] ABBOTT B P, ABBOTT R, ABBOTT T D et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102 [2] ABBOTT B P, ABBOTT R, ABBOTT T D et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral[J]. Physical Review Letters, 2017, 119(16): 161101. [3] BARACK L, CARDOSO V, NISSANKE S, et al. Black holes, gravitational waves and fundamental physics: a roadmap[J]. Classical and Quantum Gravity, 2019, 36(14): 143001. doi: 10.1088/1361-6382/ab0587 [4] DANZMANN K, RUDIGER A. LISA technology-concept, status, prospects[J]. Classical and Quantum Gravity, 2003, 20(10): S1-S9. doi: 10.1088/0264-9381/20/10/301 [5] WANNER G. Space-based gravitational wave detection and how LISA Pathfinder successfully paved the way[J]. Nature Physics, 2019, 15(3): 200-202. doi: 10.1038/s41567-019-0462-3 [6] ARMANO M, AUDLEY H, BAIRD J, et al. LISA pathfinder platform stability and drag-free performance[J]. Physical Review D, 2019, 99(8): 082001. doi: 10.1103/PhysRevD.99.082001 [7] ABICH K, BRAXMAIER C, GOHLKE M, et al. In-orbit performance of the GRACE follow-on laser ranging interferometer[J]. Physical Review Letters, 2019, 123(3): 031101. doi: 10.1103/PhysRevLett.123.031101 [8] 王智, 沙巍, 陈哲, 等. 空间引力波探测望远镜初步设计与分析[J]. 中国光学,2018,11(1):131-151. doi: 10.3788/co.20181101.0131WANG ZH, SHA W, CHEN ZH, et al. Preliminary design and analysis of telescope for space gravitational wave detection[J]. Chinese Optics, 2018, 11(1): 131-151. (in Chinese) doi: 10.3788/co.20181101.0131 [9] LUO Z R, LIU H SH, JIN G. The recent development of interferometer prototype for Chinese gravitational wave detection pathfinder mission[J]. Optics &Laser Technology, 2018, 105: 146-151. [10] 刘河山, 高瑞弘, 罗子人, 等. 空间引力波探测中的绝对距离测量及通信技术[J]. 中国光学,2019,12(3):486-492. doi: 10.3788/co.20191203.0486LIU H SH, GAO R H, LUO Z R, et al. Laser ranging and data communication for space gravitational wave detection[J]. Chinese Optics, 2019, 12(3): 486-492. (in Chinese) doi: 10.3788/co.20191203.0486 [11] LI Y P, LIU H SH, ZHAO Y, et al. Demonstration of an ultraprecise optical bench for the Taiji space gravitational wave detection pathfinder mission[J]. Applied Sciences, 2019, 9(10): 2087. doi: 10.3390/app9102087 [12] 罗子人, 张敏, 靳刚, 等. 中国空间引力波探测“太极计划”及“太极1号”在轨测试[J]. 深空探测学报,2020,7(1):3-10.LUO Z R, ZHANG M, JIN G, et al. Introduction of Chinese space-borne gravitational wave detection program “Taiji” and “Taiji-1” satellite mission[J]. Journal of Deep Space Exploration, 2020, 7(1): 3-10. (in Chinese) [13] LUO J, CHEN L SH, DUAN H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Classical and Quantum Gravity, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010 [14] SHI CH F, BAO J H, WANG H T, et al. Science with the TianQin observatory: preliminary results on testing the no-hair theorem with ringdown signals[J]. Physical Review D, 2019, 100(4): 044036. doi: 10.1103/PhysRevD.100.044036 [15] ZHANG J Y, MING M, JIANG Y Z, et al. Inter-satellite laser link acquisition with dual-way scanning for Space Advanced Gravity Measurements mission[J]. Review of Scientific Instruments, 2018, 89(6): 064501. doi: 10.1063/1.5019433 [16] FALLER J E, BENDER P L. A possible laser gravitational wave experiment in space[C]. Program and Abstracts of Second International Conference on Precision Measurement and Fundamental Constants (PMFC-II), National Bureau of Standards, 1981: 689-690. [17] TINTO M, DHURANDHAR S V. Time-delay interferometry[J]. Living Reviews in Relativity, 2014, 17: 6. doi: 10.12942/lrr-2014-6 [18] ESTABROOK F B, TINTO M, ARMSTRONG J W. Time-delay analysis of LISA gravitational wave data: elimination of spacecraft motion effects[J]. Physical Review D, 2000, 62(4): 042002. doi: 10.1103/PhysRevD.62.042002 [19] TINTO M, ESTABROOK F B, ARMSTRONG J W. Time-delay interferometry for LISA[J]. Physical Review D, 2002, 65(8): 082003. doi: 10.1103/PhysRevD.65.082003 [20] TINTO M, HARTWIG O. Time-delay interferometry and clock-noise calibration[J]. Physical Review D, 2018, 98(4): 042003. doi: 10.1103/PhysRevD.98.042003 [21] DE VINE G, RABELING D S, SLAGMOLEN B J J, et al. Picometer level displacement metrology with digitally enhanced heterodyne interferometry[J]. Optics Express, 2009, 17(2): 828-837. doi: 10.1364/OE.17.000828 [22] DE VINE G, WARE B, MCKENZIE K, et al. Experimental demonstration of time-delay interferometry for the laser interferometer space antenna[J]. Physical Review Letters, 2010, 104(21): 211103. doi: 10.1103/PhysRevLett.104.211103 [23] SPERO R, BACHMAN B, DE VINE G, et al. Progress in interferometry for LISA at JPL[J]. Classical and Quantum Gravity, 2011, 28(9): 094007. doi: 10.1088/0264-9381/28/9/094007 [24] ESTEBAN J J, GARCÍA A F, BARKE S, et al. Experimental demonstration of weak-light laser ranging and data communication for LISA[J]. Optics Express, 2011, 19(17): 15937-15946. doi: 10.1364/OE.19.015937 [25] HEINZEL G, ESTEBAN J J, BARKE S, et al. Auxiliary functions of the LISA laser link: ranging, clock noise transfer and data communication[J]. Classical and Quantum Gravity, 2011, 28(9): 094008. doi: 10.1088/0264-9381/28/9/094008 [26] BRAUSE N C. Auxiliary function development for the LISA metrology system[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2018. [27] ISLEIF K S. Laser interferometry for LISA and satellite geodesy missions[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2018. [28] SCHWARZE T S, BARRANCO G F, PENKERT D, et al. Picometer-stable hexagonal optical bench to verify LISA phase extraction linearity and precision[J]. Physical Review Letters, 2019, 122(8): 081104. doi: 10.1103/PhysRevLett.122.081104 [29] SHEARD B S, GRAY M B, MCCLELLAND D E, et al. Laser frequency stabilization by locking to a LISA arm[J]. Physics Letters A, 2003, 320(1): 9-21. doi: 10.1016/j.physleta.2003.10.076 [30] SHADDOCK D, MCKENZIE K, SPERO R, et al.. LISA frequency control white paper[R]. 2009. https://atrium.in2p3.fr/nuxeo/nxfile/default/f6aa40dc-d83b-44b2-9bd7-ee4e93d88c82/file:content/FCSTWhitePaper.pdf. [31] KARLEN L, KUNDERMANN S, TORCHEBOEUF N, et al.. Laser system for the LISA mission[C]. 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum, IEEE, 2019: 1-2. [32] CORNISH N J, HELLINGS R W. The effects of orbital motion on LISA time delay interferometry[J]. Classical and Quantum Gravity, 2003, 20(22): 4851-4860. doi: 10.1088/0264-9381/20/22/009 [33] KULLMANN J. Development of a digital phase measuring system with microradian precision for LISA[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2012. [34] GERBERDING O. Phase readout for satellite interferometry[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2014. [35] POLLACK S E, STEBBINS R T. Demonstration of the zero-crossing phasemeter with a LISA test-bed interferometer[J]. Classical and Quantum Gravity, 2006, 23(12): 4189-4200. doi: 10.1088/0264-9381/23/12/014 [36] POLLACK S E, STEBBINS R T. A demonstration of LISA laser communication[J]. Classical and Quantum Gravity, 2006, 23(12): 4201-4213. doi: 10.1088/0264-9381/23/12/015 [37] GRÜNING P, HALLOIN H, PRAT P, et al. Status of the eLISA on table (LOT) electro-optical simulator for space based, long arms interferometers[J]. Experimental Astronomy, 2015, 39(2): 281-302. doi: 10.1007/s10686-015-9448-z [38] LAPORTE B M, HALLOIN H, BRÉELLE E, et al. Status of the LISA On table experiment: a electro-optical simulator for LISA[J]. Journal of Physics:Conference Series, 2017, 840: 012014. doi: 10.1088/1742-6596/840/1/012014 [39] FRANCIS S P, SHADDOCK D A, SUTTON A J, et al. Tone-assisted time delay interferometry on GRACE Follow-On[J]. Physical Review D, 2015, 92(1): 012005. doi: 10.1103/PhysRevD.92.012005 -
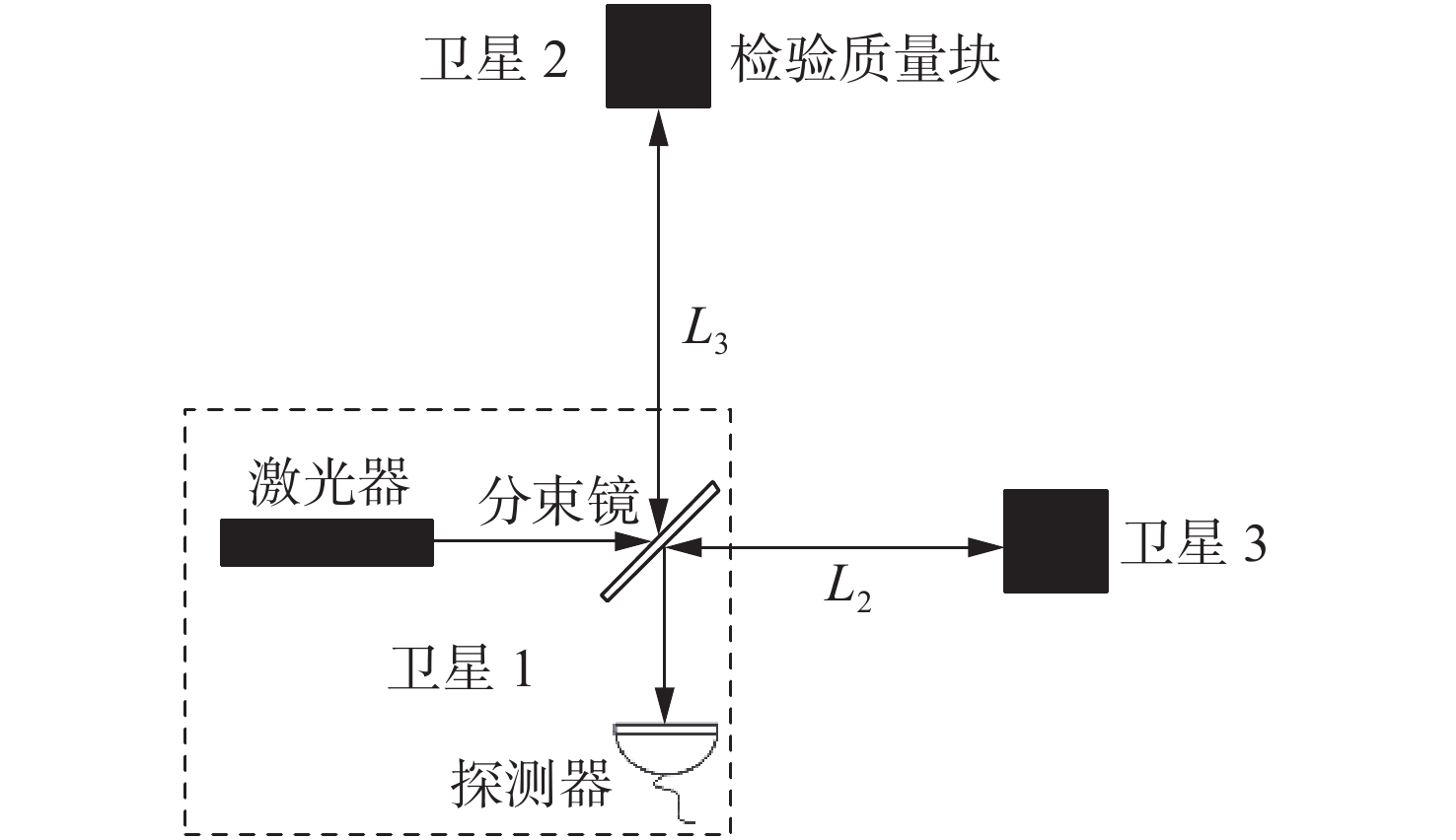
下载:
图(11)
计量
- 文章访问数: 3122
- HTML全文浏览量: 835
- PDF下载量: 360
- 被引次数: 0
