Establishment and analysis of the diffraction bidirectional reflection distribution function model for surface defects
-
摘要: 建立了包括划痕和坑点在内的表面损伤的衍射双向反射分布函数（BRDF）模型，并分析了模型在各领域中的应用。通过使用非傍轴标量衍射理论，提出了采用相干窗口函数滤波的方法得到非相干光条件下的表面损伤衍射BRDF模型，得到了表面划痕和坑点的散射特性。该方法在表面损伤检测、表面损伤杂光分析以及图像渲染技术等领域都有重要的应用价值。Abstract: The purpose of this paper is to establish a diffraction Bidirectional Reflection Distribution Function (BRDF) model of surface defects including scratches and pits, and to analyze the model being applied in various fields. By using nonparaxial scalar diffraction theory, a coherent window function filtering method is proposed, which can obtain the BRDF model of surface defect diffraction under incoherent light conditions. The effectiveness of the model is verified in related work, and the scattering characteristics of surface scratches and pits are obtained. The method and the results obtained by the model have high value in surface defect detection, surface defect stray light analysis and image rendering technology.
-
图 2 波长为（a） 0.3 μm，（b） 0.5 μm及（c） 0.8 μm的划痕仿真结果
Figure 2. Simulation results of scratches with a wavelength of (a) 0.3 μm, (b) 0.5 μm and (c) 0.8 μm
-
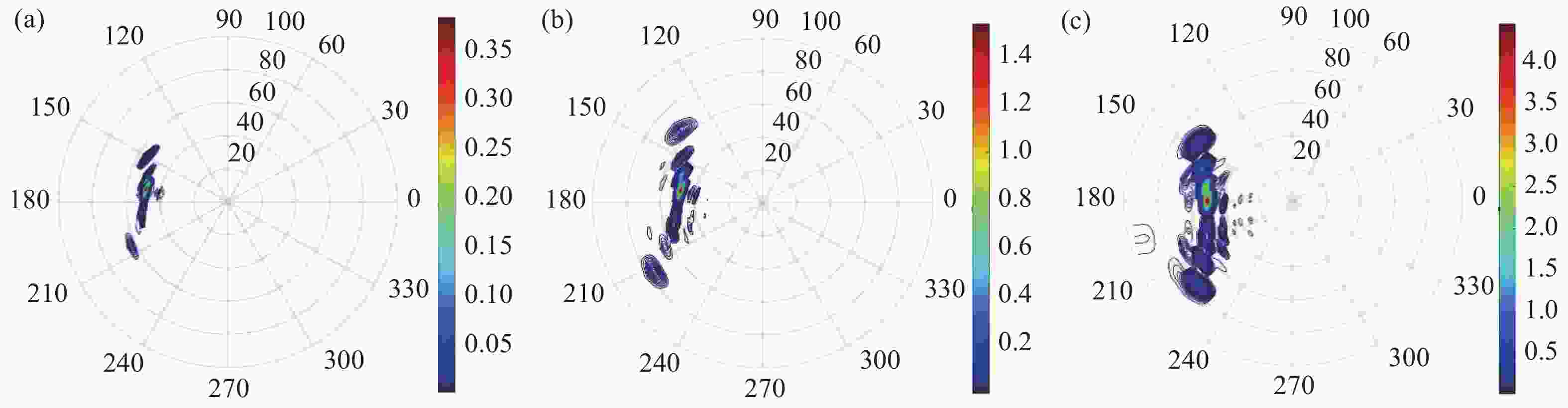
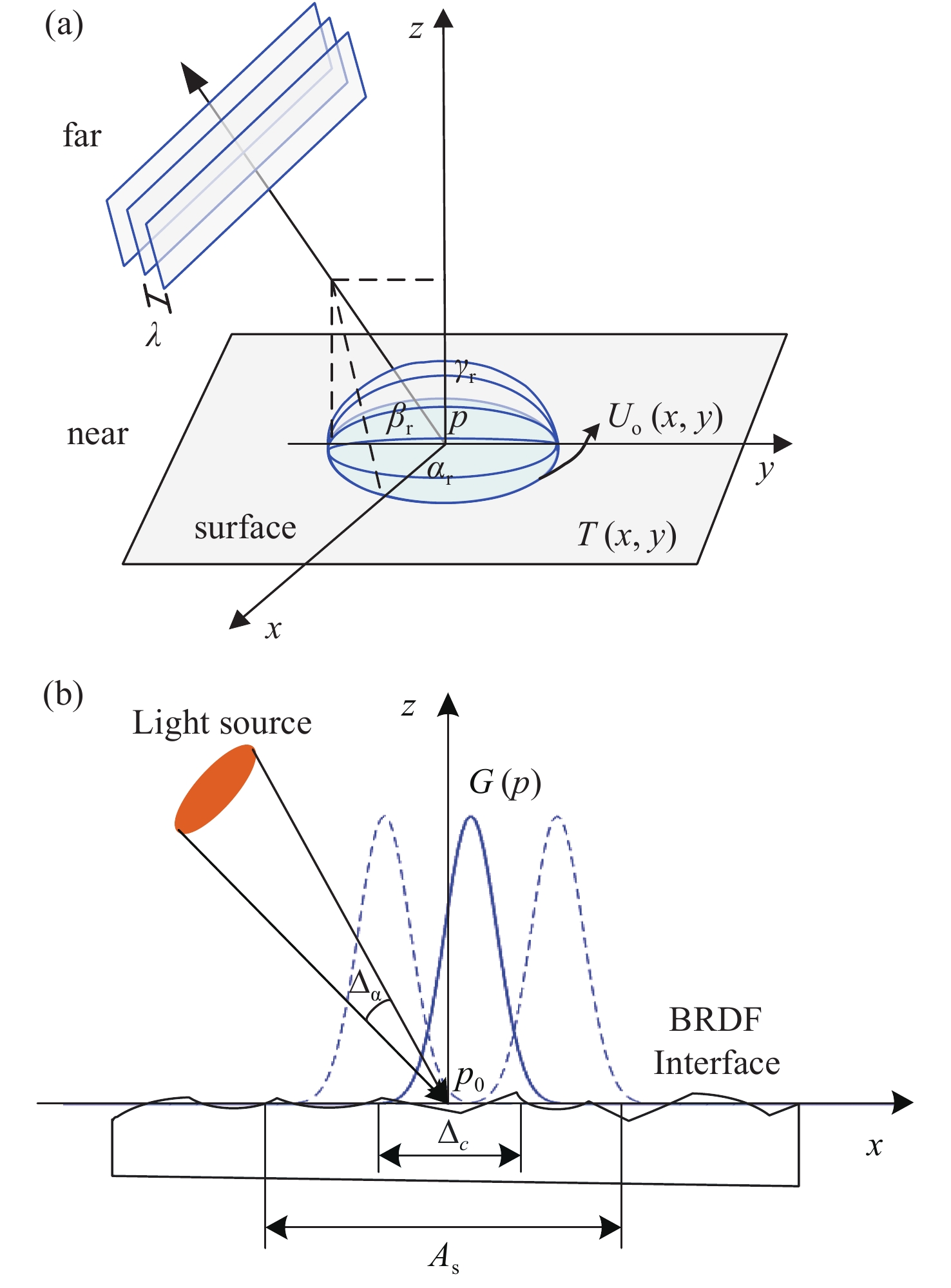
[1] LU M, WANG ZH L, WANG H L, et al. Defects scattering imaging system of 20 inch PMTs’ glass shell suitable for digital image processing[J]. Proceedings of SPIE, 2018, 10847: 108470C. [2] 陆敏, 王治乐, 高萍萍, 等. 光学元件的疵病检测及现状[J]. 光学仪器,2020,42(3):88-94.LU M, WANG ZH L, GAO P P, et al. Defect detection and current situation of optical components[J]. Optical Instruments, 2020, 42(3): 88-94. (in Chinese) [3] 王拯洲, 段亚轩, 王力, 等. 基于邻域向量内积局部对比度图像增强的光学元件损伤检测[J]. 光学 精密工程,2019,27(12):2668-2682. doi: 10.3788/OPE.20192712.2668WANG ZH ZH, DUAN Y X, WANG L, et al. Detecting optical component damage based on neighborhood vector dot contrast image enhancement[J]. Optics and Precision Engineering, 2019, 27(12): 2668-2682. (in Chinese) doi: 10.3788/OPE.20192712.2668 [4] GERMER T A. Angular dependence and polarization of out-of-plane optical scattering from particulate contamination, subsurface defects, and surface microroughness[J]. Applied Optics, 1997, 36(33): 8798-8805. doi: 10.1364/AO.36.008798 [5] PETERSON G L. A BRDF model for scratches and digs[J]. Proceedings of SPIE, 2012, 8495: 84950G. [6] HARVEY J E, VERNOLD C L, KRYWONOS A, et al. Diffracted radiance: a fundamental quantity in nonparaxial scalar diffraction theory[J]. Applied Optics, 1999, 38(31): 6469-6481. doi: 10.1364/AO.38.006469 [7] 夏志林, 曾翔, 刘世杰, 等. 基于波面面形的滤波计算[J]. 光学 精密工程,2016,24(12):3033-3040. doi: 10.3788/OPE.20162412.3033XIA ZH L, ZENG X, LIU SH J, et al. Filter calculation based on wavefront figures[J]. Optics and Precision Engineering, 2016, 24(12): 3033-3040. (in Chinese) doi: 10.3788/OPE.20162412.3033 [8] WERNER S, VELINOV Z, JAKOB W, et al. Scratch iridescence: wave-optical rendering of diffractive surface structure[J]. ACM Transactions on Graphics, 2017, 36(6): 207. [9] RAYMOND B, GUENNEBAUD G, BARLA P. Multi-scale rendering of scratched materials using a structured SV-BRDF model[J]. ACM Transactions on Graphics, 2016, 35(4): 57. [10] WEIN S J. Small-angle scatter measurement[D]. Tucson: University of Arizona, 1989. [11] 黄聪, 张科鹏, 王翔, 等. 基于总散射测量的表面质量检测新方法[J]. 光学学报,2019,39(7):0712005. doi: 10.3788/AOS201939.0712005HUANG C, ZHANG K P, WANG X, et al. Method for surface quality inspection based on total scattering measurement[J]. Acta Optica Sinica, 2019, 39(7): 0712005. (in Chinese) doi: 10.3788/AOS201939.0712005 [12] KRYWONOS A. Predicting surface scatter using a linear systems formulation of non-paraxial scalar diffraction[D]. Central Florida: University of Central Florida, 2006. [13] 高春甫, 邬敏. 粗糙表面精度测量系统的研究[J]. 光学 精密工程,2005,13(6):697-702.GAO CH P, WU M. Study of measurement system for rough surface accuracy[J]. Optics and Precision Engineering, 2005, 13(6): 697-702. (in Chinese) [14] 陆敏, 王治乐, 高萍萍, 等. 用于快速BRDF测量的子孔径扫描傅立叶变换系统[J]. 光学学报,2020,40(13):1329001. doi: 10.3788/AOS202040.1329001LU M, WANG ZH L, GAO P P, et al. A sub-aperture scanning Fourier transform system for fast BRDF measurements[J]. Acta Optica Sinica, 2020, 40(13): 1329001. (in Chinese) doi: 10.3788/AOS202040.1329001 -
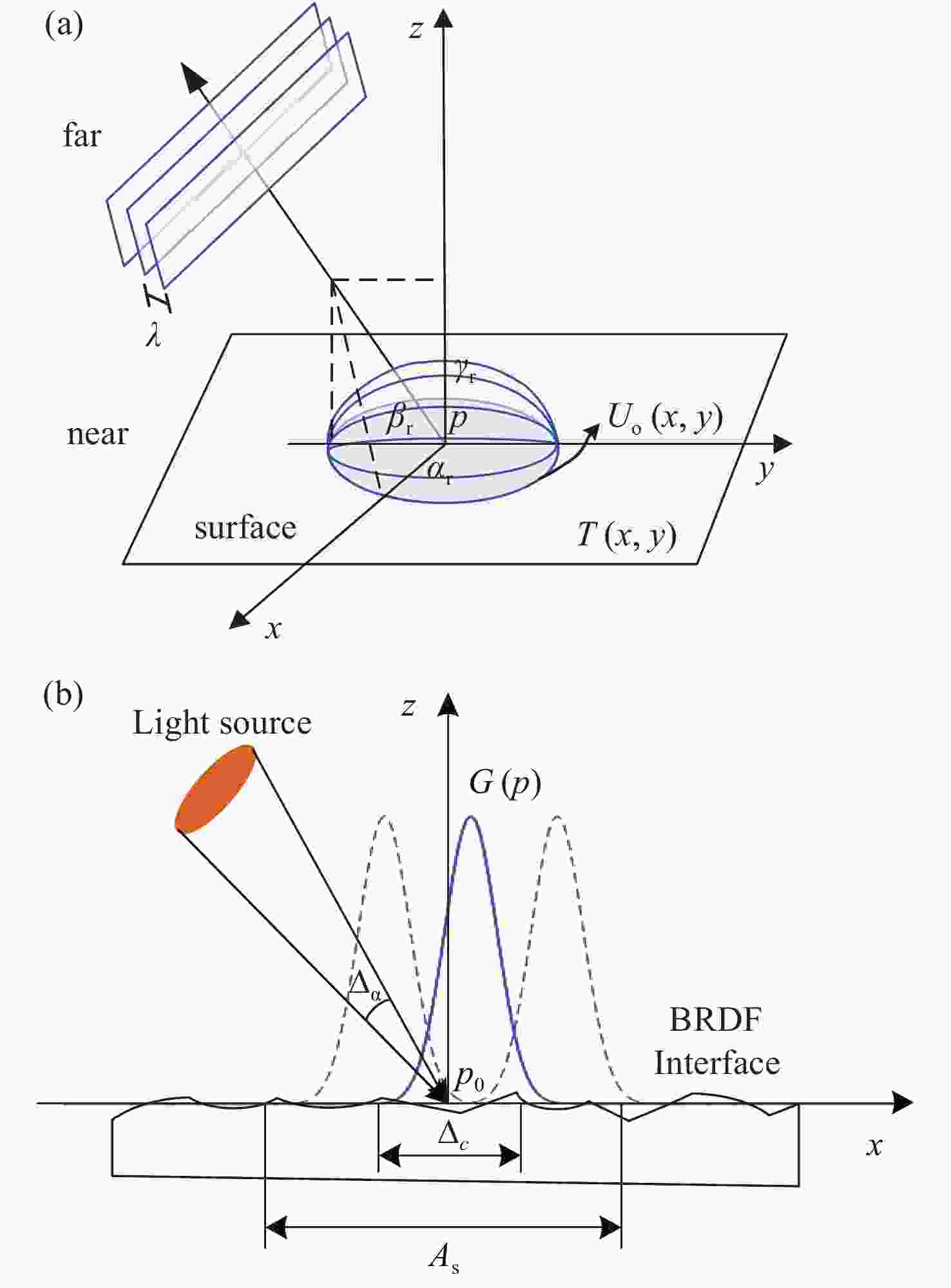
下载:
图(4)
计量
- 文章访问数: 1577
- HTML全文浏览量: 394
- PDF下载量: 77
- 被引次数: 0
