-
摘要: 激光散斑被广泛应用于生物医学，成像探测以及无损检测等应用中，为了提升目标在环系统中基于散斑统计特性反馈远场激光聚焦光斑质量的评价效率和精度。提出了多通道协同探测的方法获得回波散斑信号的时间空间融合评价因子，并对散斑场统计理论、多点协同探测系统模型和散斑时间与空间频谱融合统计特性展开深入研究。首先，利用单点探测器探测动态散斑的强度波动信号，对其进行滤波、自相关和傅立叶变换后获得散斑场的功率谱，再乘以权重获得散斑评价因子，探究该评价因子监视远场光斑的可行性。然后，提出对探测面不同空间位点获得的时间信号进行拼接的方法，并列举实现该方法的先决条件。最后，通过仿真与实验验证利用散斑场融合频谱获得评价因子的有效性。结果表明，动态散斑评价因子随目标光斑尺寸的增加而减小，当探测面上4通道协同获取的信号不相关时，评价因子取平均可使精度提高2倍，而时间空间融合频谱获得的评价因子可保证精度的同时使系统带宽提高4倍。综上所述，多点协同获取的散斑评价因子可以更快速的监视远距离运动目标的光斑变化。Abstract: To improve the accuracy and efficiency of the dynamic speckle metric for non-destructively detecting far-field target hit-spot intensity in a Target-In-the-Loop (TIL) system, a multi-channel cooperative detection system for acquiring speckle signals is established. The theory of dynamic speckles, the simulation model of this system and the spatial-temporal spectral fusion characteristics are also investigated. As a first step, the power spectrum is obtained by filtering, auto-correlating and Fourier transforming the intensity fluctuations of dynamic speckle detected by the point detector. Then, the feasibility of speckle-metric, obtained by multiplying the spectrum with weights, is explored to monitor the target-focused spot. As a second step, the approach of splicing the temporal signals obtained from different spatial locations on the receiving plane is proposed. Moreover, the prerequisites of this approach are listed. Finally, the effectiveness of the proposed speckle metric obtained by fusing the spectrum is verified through simulations and experiments. The results show that the speckle metric decreases with an increase in the hit-spot size, and the four-channel space-averaging metric can improve the accuracy by a factor of 2 when each group of signals is uncorrelated. Moreover, the metric obtained by spatial-temporal fusion spectrum not only guarantees accuracy but also quadruples the system’s bandwidth. Therefore, the multi-channel cooperative acquisition of the speckle metric can monitor the hit-spot change of far-field moving targets more rapidly than current solutions.
-
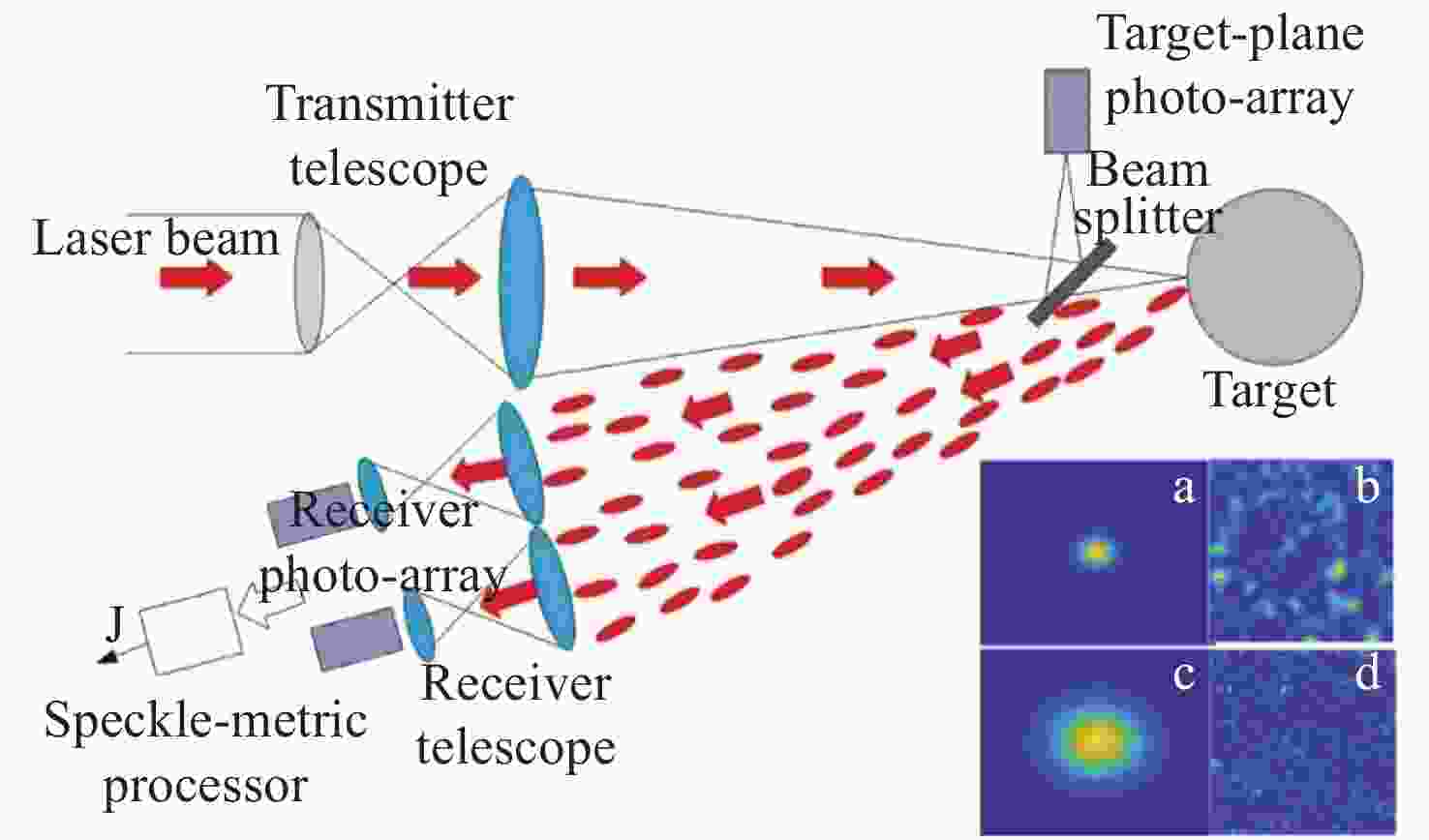
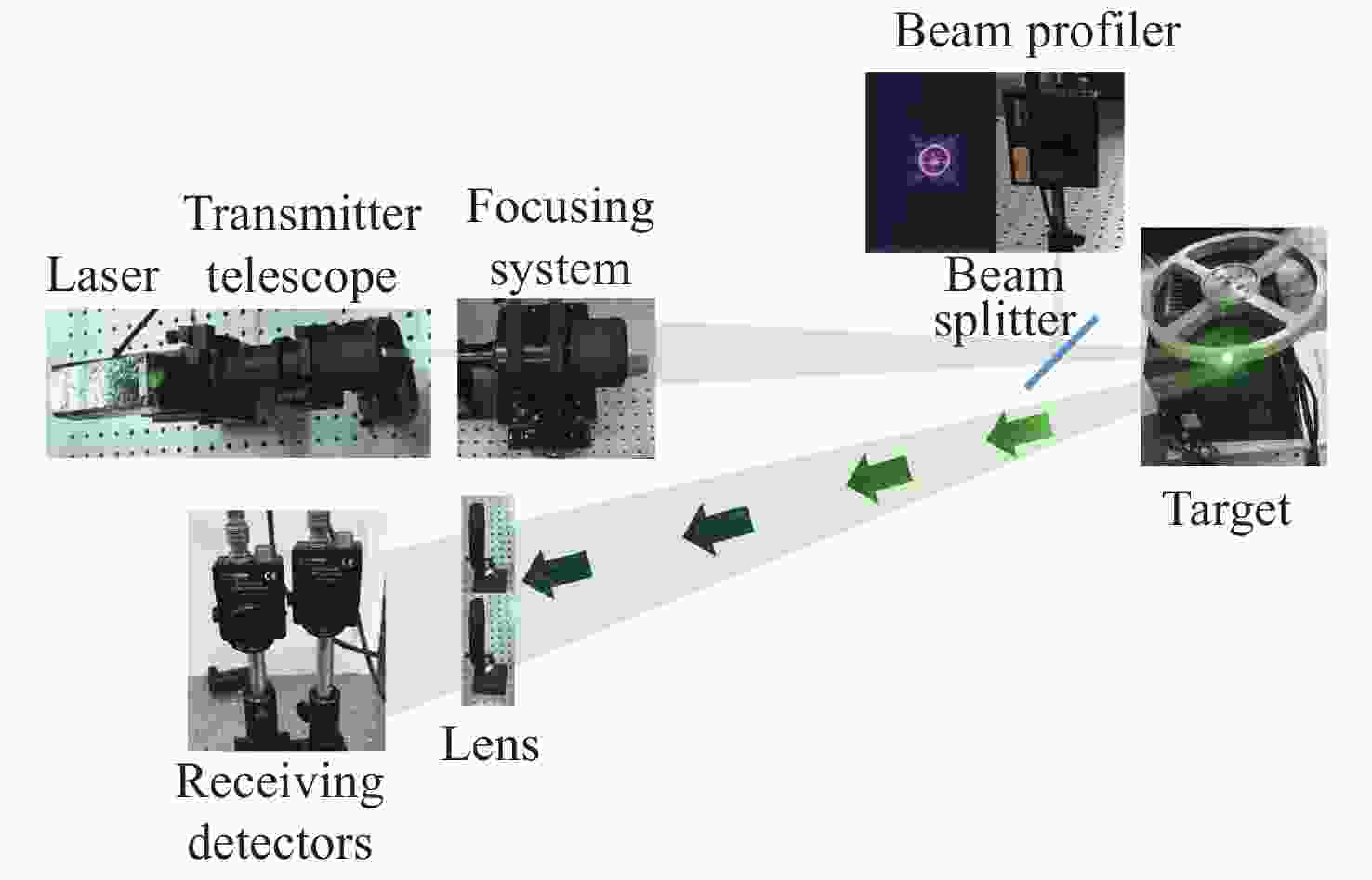
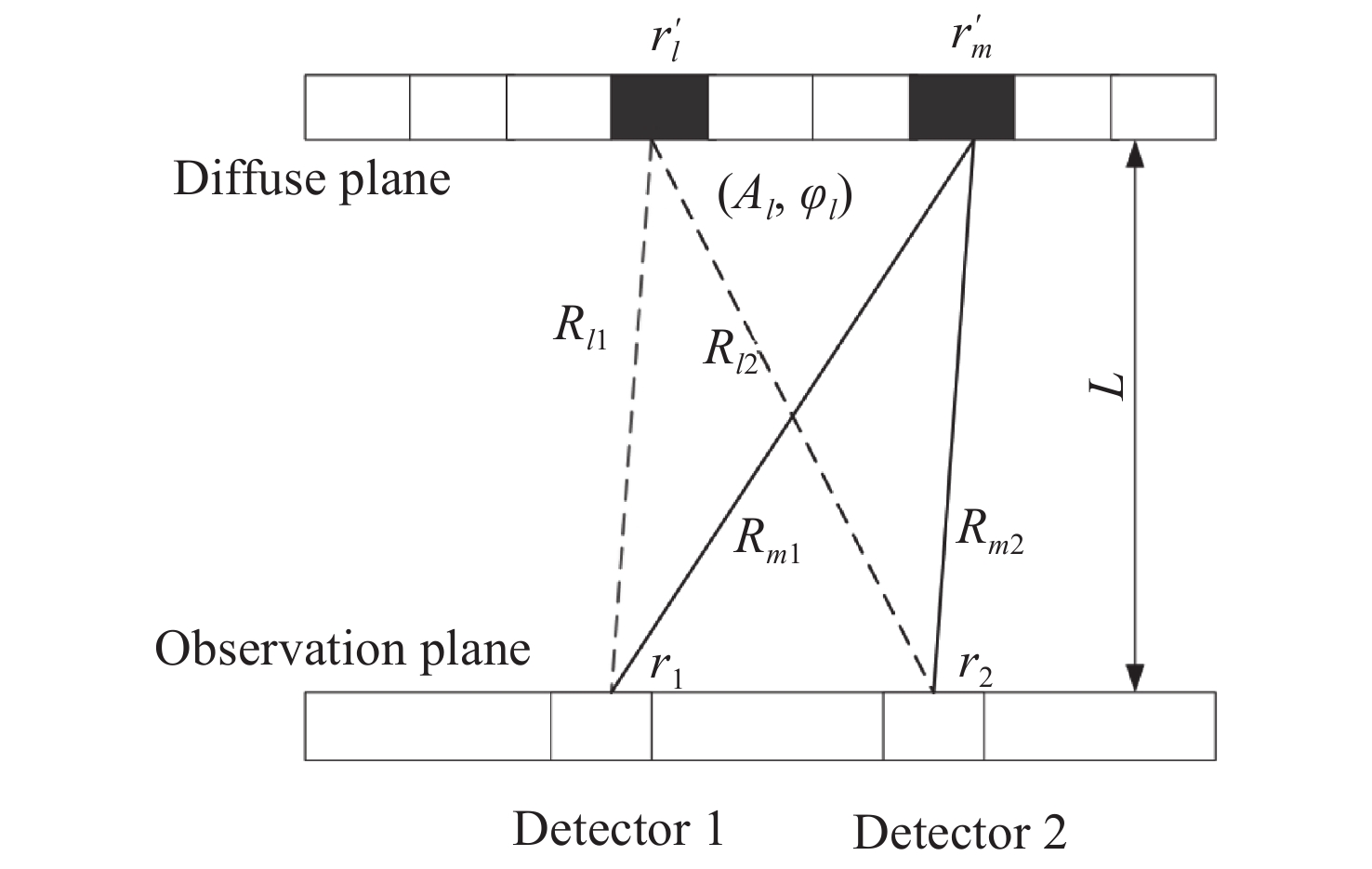
图 2 TIL系统的光学布局图。出射激光复振幅A(r')通过均匀介质聚焦到目标靶面上，经粗糙表面散射后，回波由多个信号不相关的探测器接收。（a）目标粗糙表面直径为1.5 mm的聚焦光斑；（b）1.5 mm目标光斑对应的散斑光强；（c）目标粗糙表面直径为4 mm的聚焦光斑；（d）4 mm目标光斑对应的散斑光强。
Figure 2. TIL wave propagation configurations. Transmitted wave with complex amplitude A(r') propagates in an optically homogeneous medium toward a target, and after scattering off the target surface at the plane (r', z=L), the return wave propagates back to the multi-channel detectors. (a) Spot with a diameter of 1.5 mm focused on the target. (b) The speckle pattern corresponds to (a). (c) Spot with a diameter of 4 mm focused on the target, and (d) shows the speckle pattern corresponding to (c).
图 3 动态散斑强度波动归一化互相关函数仿真结果。（a）ρ=3 m；（b）ρ=6 m
Figure 3. The simulation results of the dynamic speckles normalized cross-correlation function. (a) ρ=3 m; (b) ρ=6 m
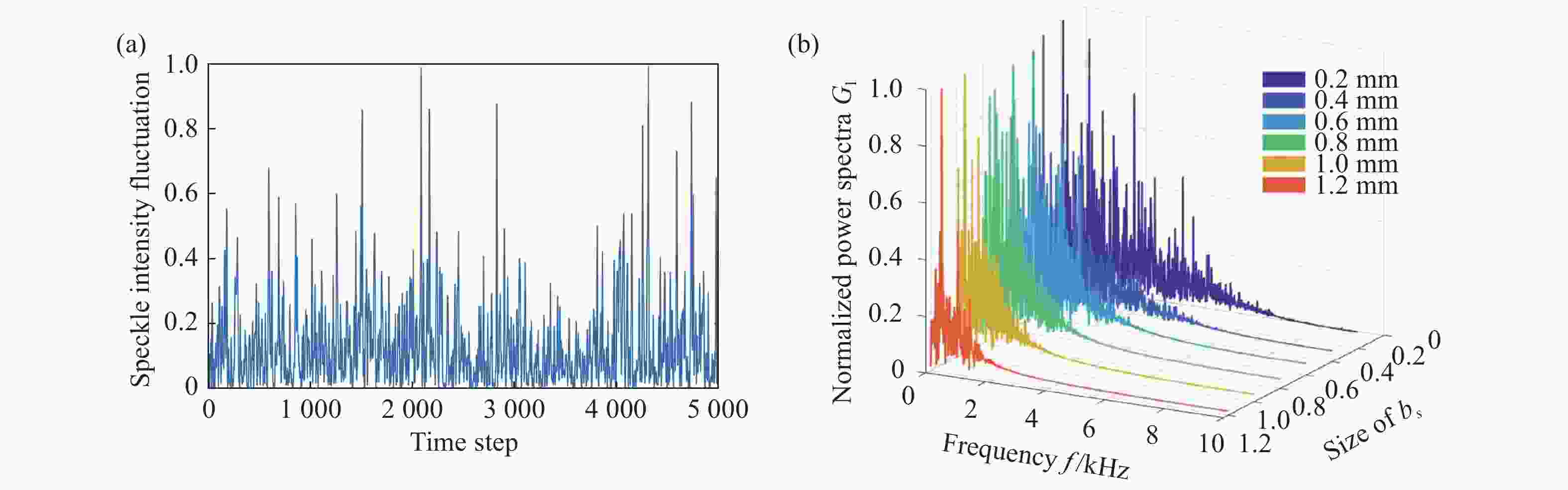
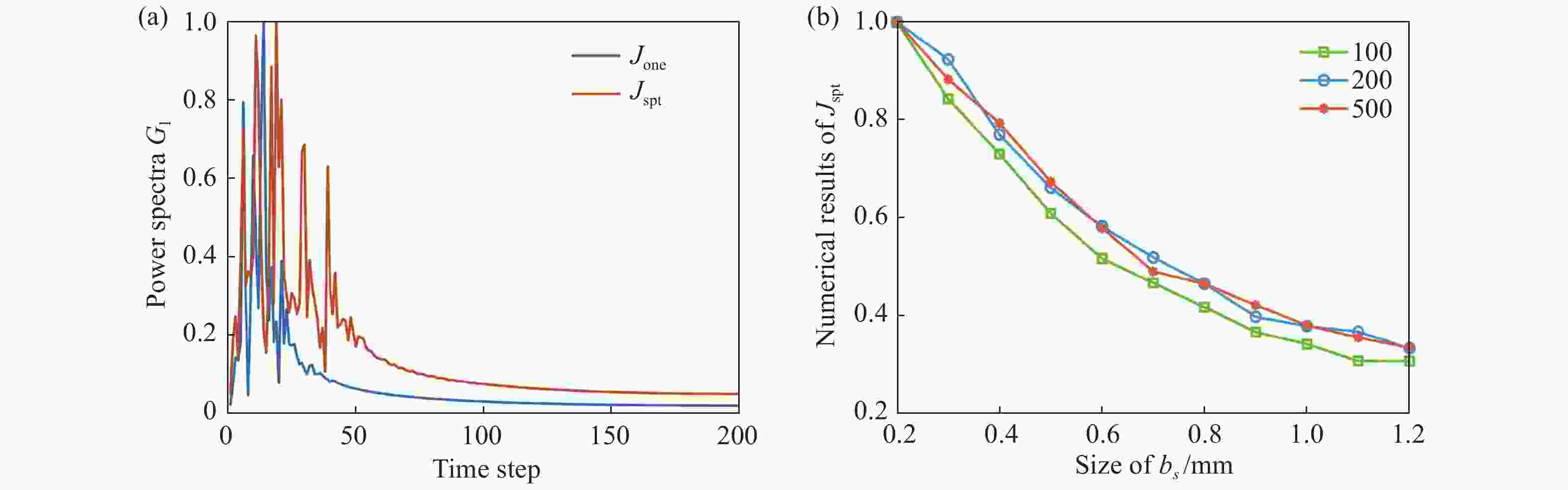
图 4 根据点运动模型探测的动态散斑信号。（a）探测面一定孔径内的散斑强度波动信号；(b)目标光斑半径由0.2 mm逐步变为1.2 mm时，对应的散斑功率谱带宽逐渐缩短。
Figure 4. The dynamic speckle signals according to the model of the movement of Scatters. (a) Speckle signal fluctuations. (b) The frequency bandwidth of the power spectra decreases as the target spot size changes from 0.2 mm to 1.2 mm
图 5 评价因子随目标光斑尺寸变化的仿真结果。目标光斑半径从0.2 mm变为1.2 mm，间隔为0.01 mm
Figure 5. Simulation results of the speckle-metric varying with the target spot size from 0.2 mm to 1.2 mm, with an interval of 0.01 mm
图 6 （a）单通道获得的时间频谱和4通道获得的时间空间频谱。（b）四通道获得的归一化评价因子随目标光斑尺寸的变化
Figure 6. (a) Temporal spectrum obtained by a single-channel, and the spatio-temporal spectrum obtained by a four-channel. (b) The normalized speckle-metric obtained by the four-channel varying with the target spot size
图 7 两个单点探测器采集激光回波散斑的实验平台
Figure 7. Experimental platform for collecting laser echo speckle with two single-point detectors
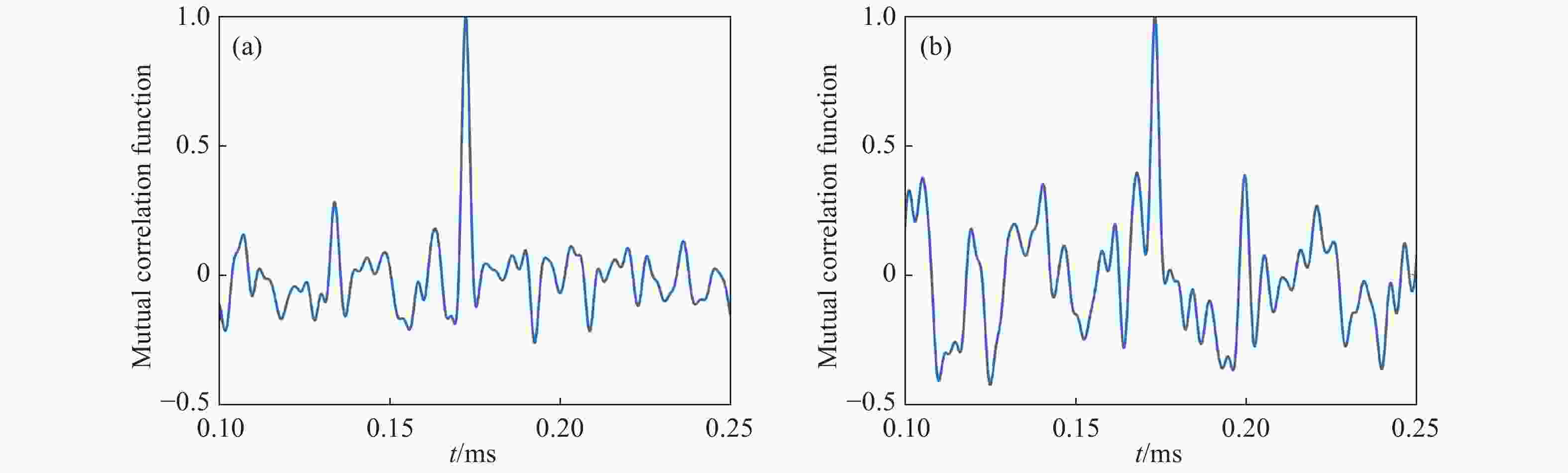
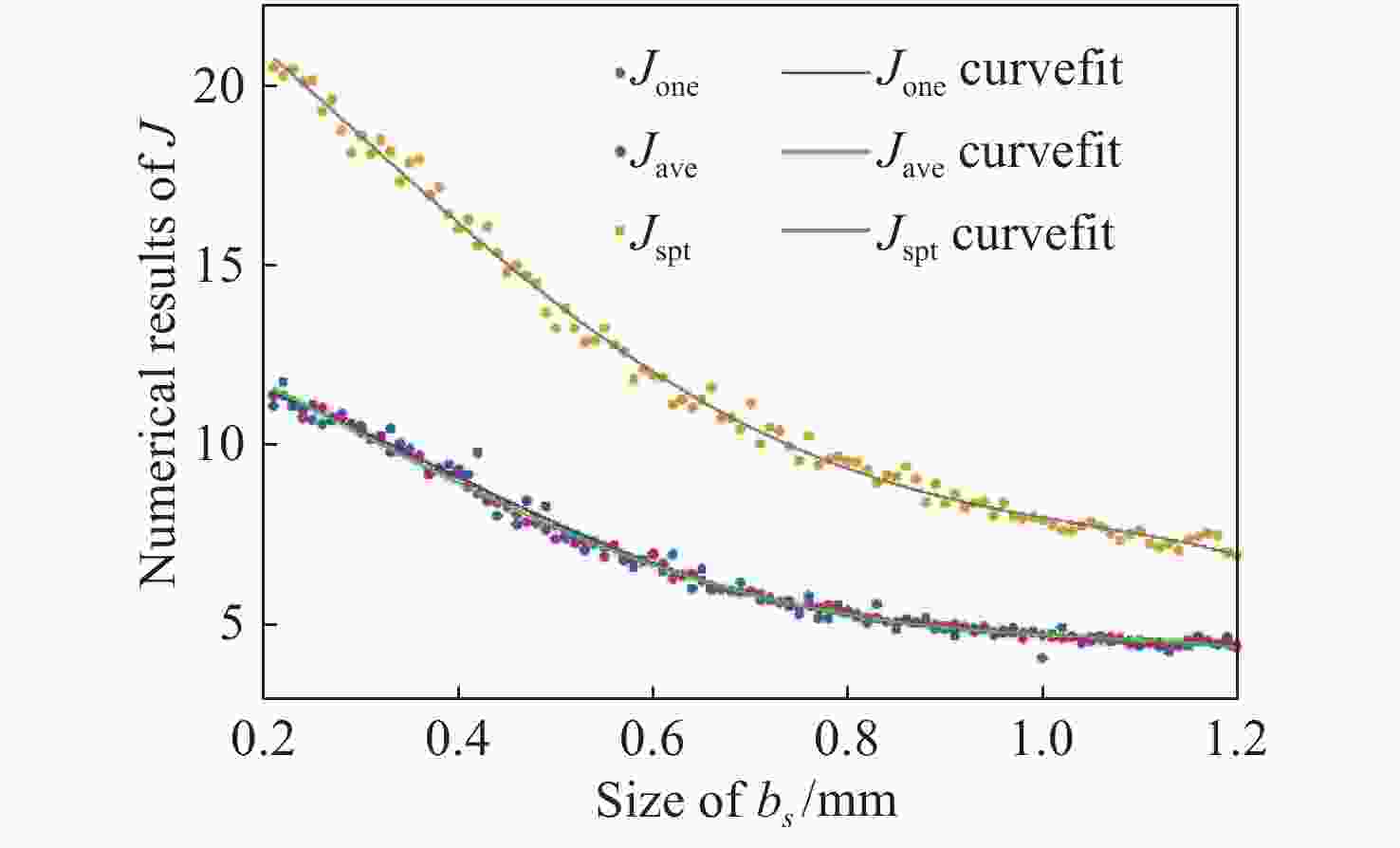
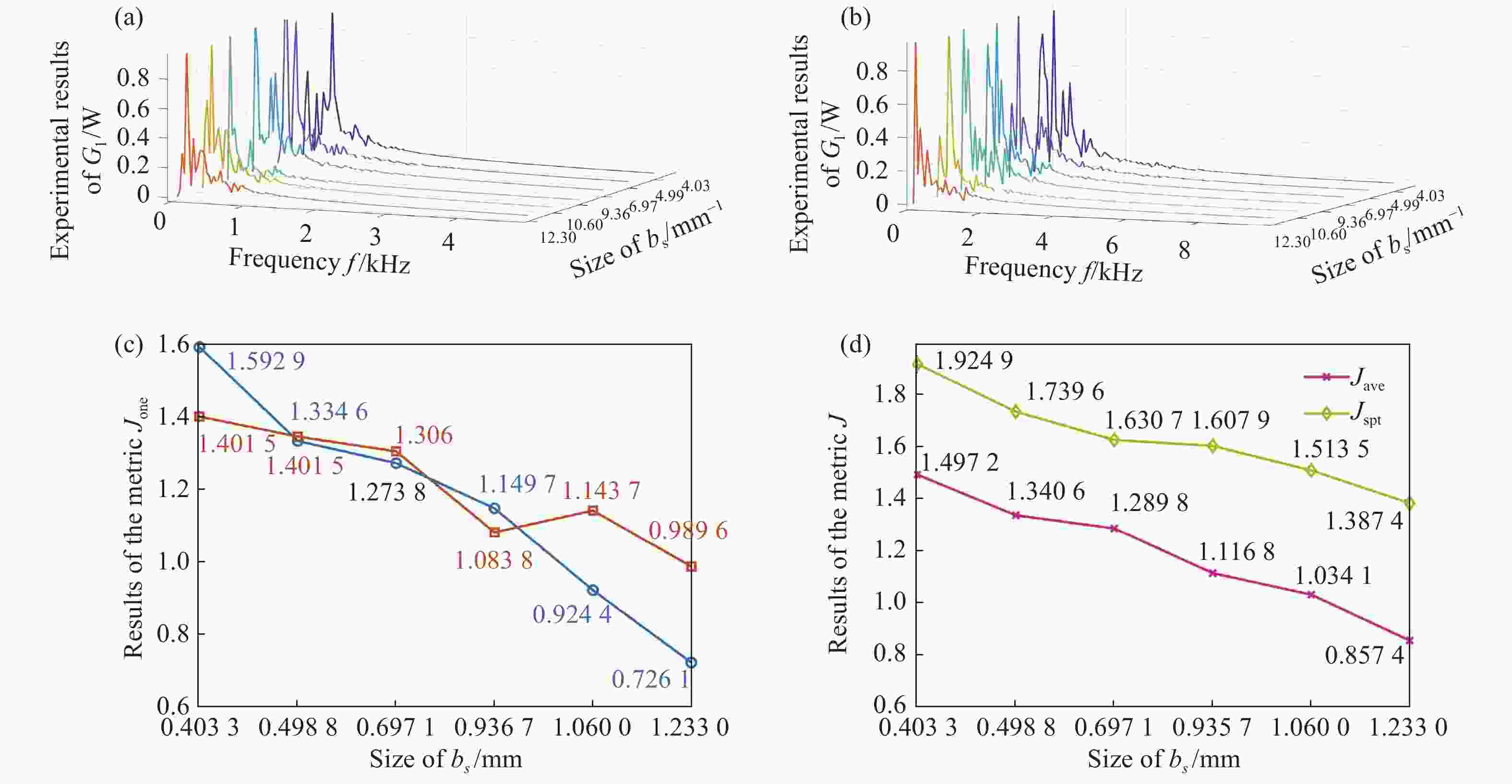
图 8 散斑强度频谱法实验结果，（a）和（b）中横坐标表示强度波动的频率，纵坐标为两个探测器获得的归一化时间频谱。（c）两个单点探测器获得的评价因子Jone实验结果，（d）对应两通道的实验结果取平均获得评价因子Jave和融合空间时间频谱的评价因子Jspt.
Figure 8. Experimental results of the speckle spectroscopy method. The horizontal coordinates in (a) and (b) indicate the frequency of intensity fluctuations, and the vertical coordinates are the normalized temporal spectra obtained from the two detectors. (c) Results of the speckle-metric Jone obtained by two point detectors, and (d) shows the speckle-metrics obtained by averaging the two-channel results (Jave) and the spatial-temporal spectrum (Jspt).
表 1 拟合信息
Table 1. Fitting results
curve R2 RMSE Jone 0.9888 2.311 Jave 0.9972 1.123 Jspt 0.9949 2.909 
下载: 导出CSV
-
[1] Stoykova E, Kang H, Kim Y, et al. Evaluation of activity from binary patterns in dynamic speckle analysis[J]. Optics and Lasers in Engineering, 2018, 111: 50-57. doi: 10.1016/j.optlaseng.2018.07.020 [2] Zhang Y, Ceylan Koydemir H, Shimogawa M M, et al. Motility-based label-free detection of parasites in bodily fluids using holographic speckle analysis and deep learning[J]. Light: Science & Applications, 2018, 7(1). [3] Wan Y, Fan X, Wang S, et al. Wavemeter capable of simultaneously achieving ultra-high resolution and broad bandwidth by using Rayleigh speckle from single mode fiber[J]. Journal of Lightwave Technology, 2021, 39(7): 2223-2229. doi: 10.1109/JLT.2020.3046022 [4] Mendoza-Herrera L J, Schinca D C, Scaffardi L B, et al. Measurement of latex microparticle size by dynamic speckle technique[J]. Optics and Lasers in Engineering, 2021, 140: 106528. doi: 10.1016/j.optlaseng.2020.106528 [5] 胡慧然, 但西佐, 赵琪涵, 等. 数字图像相关中的散斑区域自动提取研究[J]. 中国光学,2019,12(6):1329-1337. doi: 10.3788/co.20191206.1329Hu H R, Dan X Z, Zhao Q H. et al. Automatic extraction of speckle area in digital image correlation[J]. Chinese Optics, 2019, 12(6): 1329-1337. (in Chinese) doi: 10.3788/co.20191206.1329 [6] Salter P S, Booth M J. Adaptive optics in laser processing[J]. Light: Science & Applications, 2019, 8(1). [7] Piatrou P, Roggemann M. Beaconless stochastic parallel gradient descent laser beam control: numerical experiments[J]. Applied optics, 2007, 46(27): 6831-6842. doi: 10.1364/AO.46.006831 [8] Che D, Li Y, Wu Y, et al. Theory of AdmSPGD algorithm in fiber laser coherent synthesis[J]. Optics Communications, 2021, 492: 126953. doi: 10.1016/j.optcom.2021.126953 [9] Wan Y, Wang S, Fan X, et al. High-resolution wavemeter using Rayleigh speckle obtained by optical time domain reflectometry[J]. Optics letters, 2020, 45(4): 799-802. doi: 10.1364/OL.384248 [10] Budini, Nicolas, Balducci N, Mulone C, et al. Extraction of dynamic speckle activity information from digital holograms[J]. Optical Engineering, 2016, 55.12: 121716. [11] Davila A, Rayas J A. Single-shot phase detection in a speckle wavemeter for the measurement of femtometric wavelength change[J]. Optics and Lasers in Engineering, 2020, 125(Feb.): 105856.1-105856.5. [12] Kulkarni R, Pal P, Banoth E. Spatio-temporal analysis of dynamic speckle patterns using singular value decomposition[J]. Optics and Lasers in Engineering, 2021, 142: 106588. doi: 10.1016/j.optlaseng.2021.106588 [13] 邵珩, 周勇, 祁俊峰, 等. GPU加速电子剪切散斑干涉图像处理[J]. 液晶与显示,2019,34(10):1021-1029. doi: 10.3788/YJYXS20193410.1021Shao H, Zhou Y, Qi J F. et al. GPU accelerated image processing for electronic speckle pattern shearing interferometry[J]. Chinese Journal of Liquid Crystals and Displays., 2019, 34(10): 1021-1029. (in Chinese) doi: 10.3788/YJYXS20193410.1021 [14] Sawatari T, Elek A C. Image plane detection using laser speckle patterns[J]. Applied optics, 1973, 12(4): 881-883. doi: 10.1364/AO.12.000881 [15] 阳志强, 吴振森, 张耿. 旋转圆锥目标动态散斑的时间相关函数[J]. 光学学报,2013,33(10):1029001. doi: 10.3788/AOS201333.1029001Yang Z Q, Wu Z S, Zhang Q, et al. Time correlation function of dynamic speckle of rotating cone target[J]. Acta Optica Sinica, 2013, 33(10): 1029001. (in Chinese) doi: 10.3788/AOS201333.1029001 [16] Xu X, Ren X, Zhong F, et al. Optimization of speckle pattern based on integer programming method[J]. Optics and Lasers in Engineering, 2020, 133: 106100. doi: 10.1016/j.optlaseng.2020.106100 [17] Skipetrov S E, Peuser J, Cerbino R, et al. Noise in laser speckle correlation and imaging techniques[J]. Optics express, 2010, 18(14): 14519-14534. doi: 10.1364/OE.18.014519 [18] Stoykova E, Berberova N, Kim Y, et al. Dynamic speckle analysis with smoothed intensity-based activity maps[J]. Optics &Lasers in Engineering, 2017, 93: 55-65. [19] Semenov D V, Miridonov S V, Nippolainen E, et al. Statistical properties of dynamic speckles formed by a deflecting laser beam[J]. Optics express, 2008, 16(2): 1238-1249. doi: 10.1364/OE.16.001238 [20] Miridonov S V, Sidorov I, Nippolainen E, et al. Accuracy of measuring systems using dynamic speckles[J]. JOSA A, 2009, 26(4): 745-753. doi: 10.1364/JOSAA.26.000745 [21] Vorontsov M A, Kolosov V V, Polnau E. Target-in-the-loop wavefront sensing and control with a Collett-Wolf beacon: speckle-average phase conjugation[J]. Applied optics, 2009, 48(1): A13-A29. doi: 10.1364/AO.48.000A13 [22] Vorontsov M, Weyrauch T, Lachinova S, et al. Speckle-metric-optimization-based adaptive optics for laser beam projection and coherent beam combining[J]. Optics letters, 2012, 37(14): 2802-2804. doi: 10.1364/OL.37.002802 [23] Yin W, Zhong J, Feng S, et al. Composite deep learning framework for absolute 3D shape measurement based on single fringe phase retrieval and speckle correlation[J]. Journal of Physics Photonics, 2020, 2: 45009. doi: 10.1088/2515-7647/abbcd9 [24] 张亚超, 刘鹏, 王晓光, 等. X射线散射法测量Wolter-I型掠入射望远镜的表面粗糙度[J]. 中国光学,2019,12(003):587-595. doi: 10.3788/co.20191203.0587Zhang Y C, Liu P, Wang X G. et al. Characterizing curved surface roughness of Wolter-ⅠX-ray grazing incidence telescope[J]. Chinese Optics, 2019, 12(003): 587-595. (in Chinese) doi: 10.3788/co.20191203.0587 [25] Rytov S M, Kravtsov Y A, Tatarskii V I. Principles of statistical radiophysics. 4. Wave propagation through random media[M]. 1989. [26] Vorontsov M A. Speckle effects in target-in-the-loop laser beam projection systems[J]. Advanced Optical Technologies, 2013, 2(5-6): 369-395. [27] Yu, Z. , Guo, J., Liu, L., Wang, et al. Statistical properties of dynamic speckles in application to laser focusing systems[J]. Applied Optics, 2019, 58(12): 3310-3316. doi: 10.1364/AO.58.003310 [28] Dainty J C, Ennos A E, Françon M, et al. Laser Speckle and Related Phenomena[J]. Optica Acta International Journal of Optics, 1976, 23(10): 842-843. [29] Rabal H J, Arizaga R, Cap N L, et al. Numerical model for dynamic speckle: an approach using the movement of the scatterers[J]. Journal of Optics A:Pure and Applied Optics, 2003, 5(5): S381. doi: 10.1088/1464-4258/5/5/396 [30] 钱伟, 蒋明. 数字图像相关方法中数字散斑场的制作与应用研究[J]. 液晶与显示,2020(8):861-869. doi: 10.37188/YJYXS20203508.0861Qian W, Jiang M. Design and application of digital speckle patterns in digital image correlation method[J]. Chinese Journal of Liquid Crystals and Displays, 2020(8): 861-869. (in Chinese) doi: 10.37188/YJYXS20203508.0861 [31] S. A. Akhmanov, Y. E. D’yakov and A. S. Chirkin, Introduction to Statistical Radiophisics and Optics[M]. 1981 -
下载:
计量
- 文章访问数: 965
- HTML全文浏览量: 533
- PDF下载量: 130
- 被引次数: 0
