Polarization aberration analysis of catadioptric anamorphic optical systems and its effect on the point spread function
-
摘要:
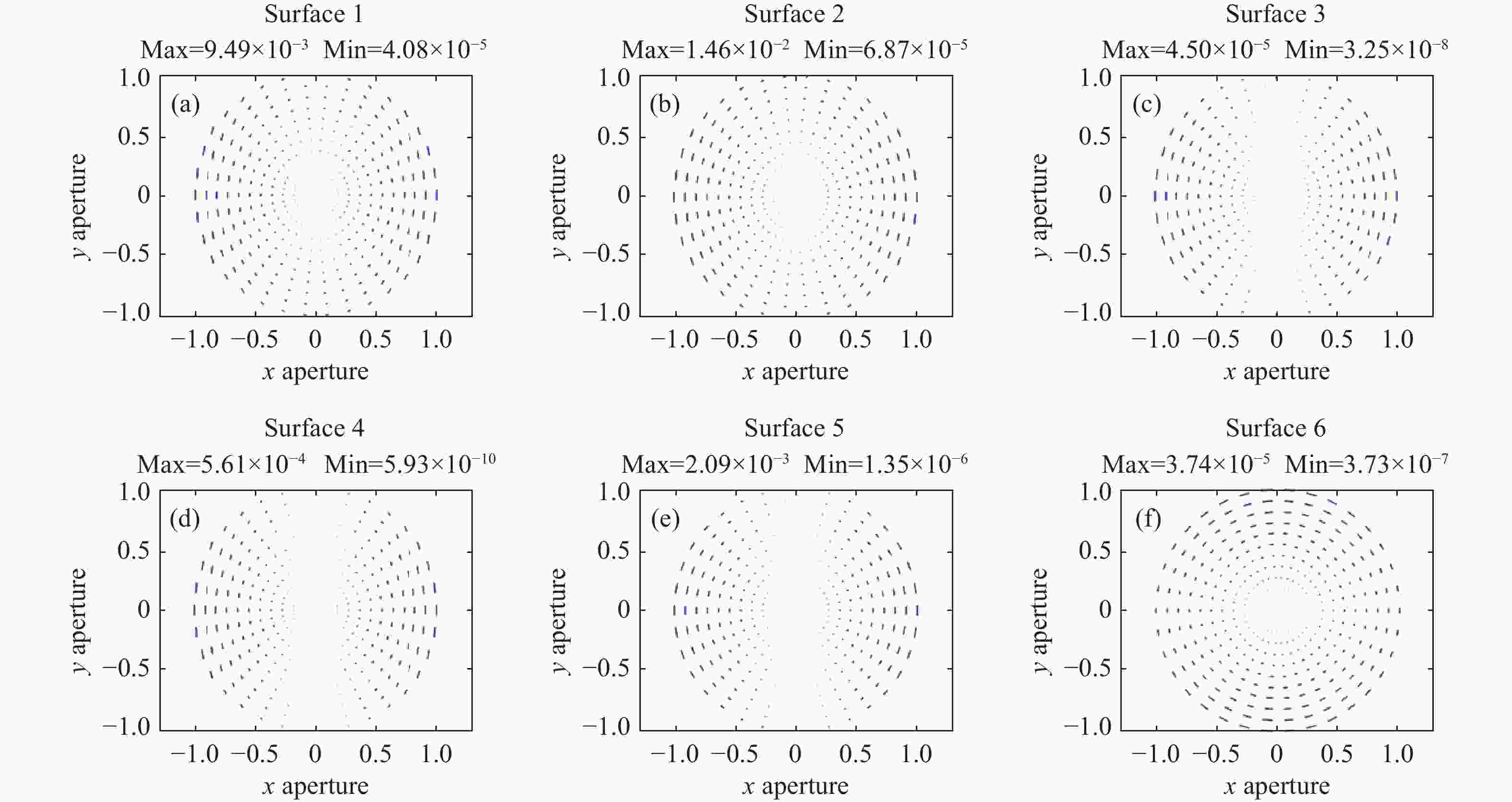
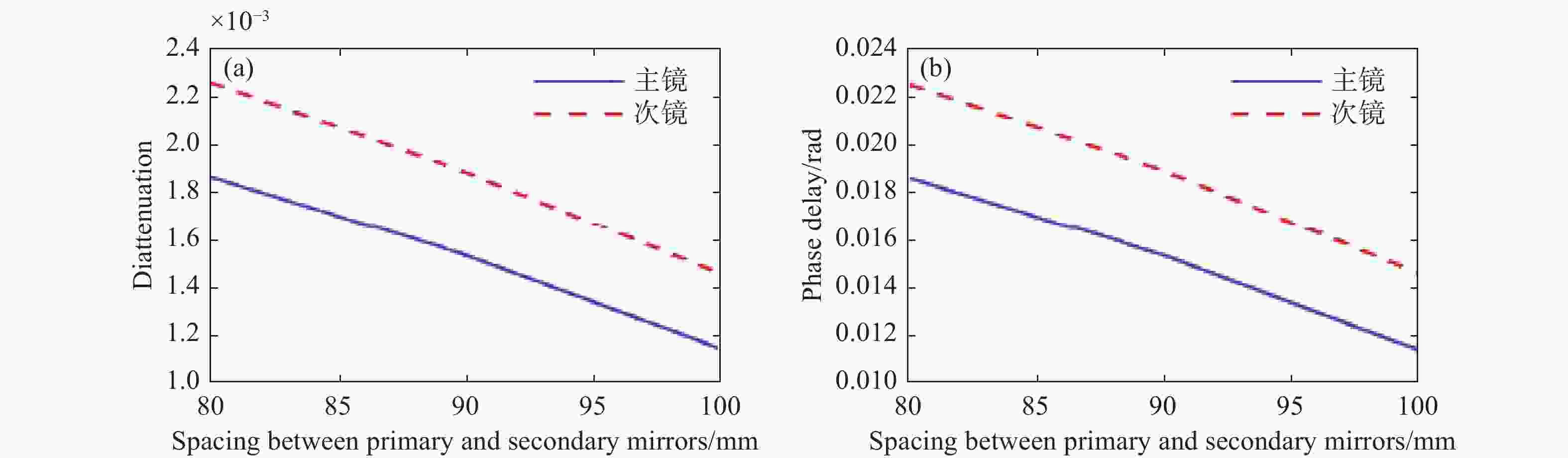
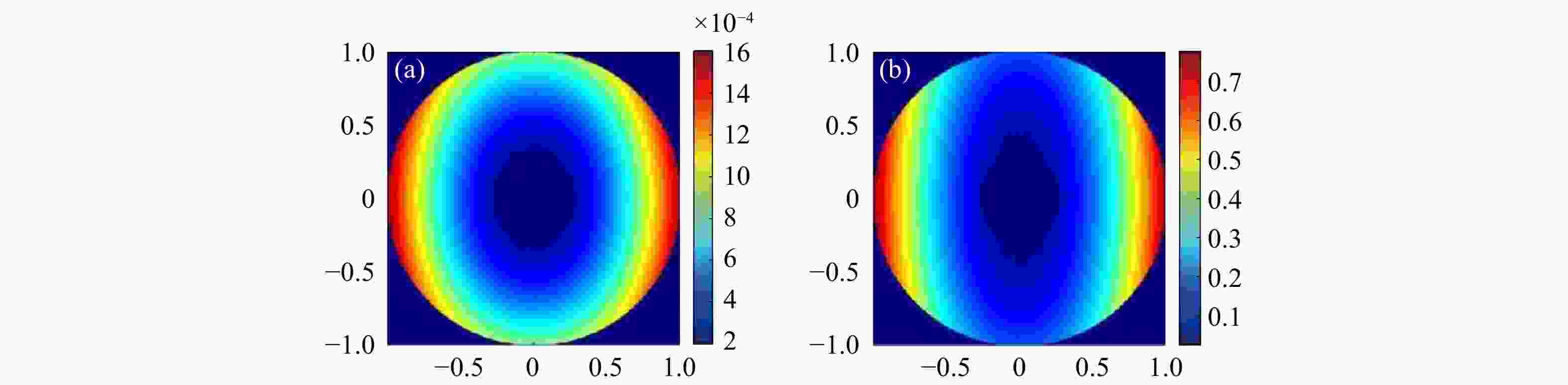
变形光学系统是一种具有双平面对称性的相对特殊的光学系统，其结构会引入非旋转对称的偏振像差。针对这一问题，本文构建一个折反式变形光学系统，并对该系统的偏振像差及其对点扩散函数的影响进行系统分析。基于三维偏振光线追迹对折反式变形光学系统进行仿真计算，获得偏振像差的详细数据，并计算各个表面的二向衰减、相位延迟分布特性以及系统的琼斯瞳、振幅响应矩阵、点扩散函数和偏振串扰对比度。结果表明：最大二向衰减为0.145，最大相位延迟为1.46×10−2 rad，均出现在次镜位置。2∶1变形比的光学系统的振幅响应函数在长焦端和短焦端方向的偏振串扰项存在40.6%的差异，偏振串扰将该变形光学系统的对比度限制在10−6量级。高精度变形光学系统中的偏振像差不可忽略，可采用膜层设计和折反式结构等方法降低偏振像差影响。该研究结论可为变形光学系统在深空探测、相干通信系统等领域的设计提供参考。
Abstract:The anamorphic optical system is a relatively special optical system with bi-planar symmetry, whose structure gives rise to non-rotationally symmetric polarization aberrations. Aiming at the problem, we construct a catadioptric anamorphic optical system. Furthermore, we also systematically analyzes the polarization aberration of this system and its effect on the point spread function. Simulations of a catadioptric anamorphic optical system based on a three-dimensional polarized light trace are performed to obtain detailed data on the polarization aberration and to compute the diattenuation and retardance distribution characteristics of individual surfaces, as well as the Jones pupil, the amplitude response matrix, the point spread function, and the polarization crosstalk contrast of the system. The maximum diattenuation is 0.145, and the maximum retardance is 1.46×10−2 rad, both occurring at the secondary mirror position. The amplitude response function of the optical system with a 2∶1 anamorphic ratio has a 40.6% difference between the polarization crosstalk term in the long and short focal end directions, and the anamorphic optical systems contrast is limited by an order of magnitude of 10−6 by polarization crosstalk. Polarization aberration in high-precision anamorphic optical systems is not negligible. The effects of polarization aberration can be reduced by film layer design and catadioptric structure. The conclusions of this study can serve as a reference for designing anamorphic optical systems in deep space exploration and coherent communication systems.
-
图 1 铝反射膜的 (a)反射系数及(b)相位随入射角变化曲线
Figure 1. Variations of (a) reflection coefficients and (b) phase with incident angle of aluminum reflection film
图 2 增透膜的 (a)透射系数 ts、tp 及(b)相位
$\phi_{\mathrm{s}} $ 、$\phi_{\mathrm{p}} $ 随入射角的变化曲线Figure 2. Variations of (a) transmission coefficients ts, tp and (b) phase transmission
$\phi_{\mathrm{s}} $ ,$\phi_{\mathrm{p}} $ with incident angle of AR coating
图 5 折返式变形光学系统各个光学表面的中心二向衰减分布图。(a) M1；(b) M2；(c) L1前表面；(d) L1后表面；(e) L2前表面；(f) L2后表面
Figure 5. Diattenuation maps for each mirror and lens element in the designed catadioptric anamorphic optical system. (a) M1; (2) M2; (c) L1 front; (d) L1 rear; (e) L2 front; (f) L2 rear
图 6 折反式变形光学系统各个光学表面的中心视场相位延迟分布图。(a) M1；(b) M2；(c) L1前表面；(d) L1后表面；(e) L2前表面；(f) L2后表面
Figure 6. Retardance maps for each mirror and lens element in the designed catadioptric anamorphic optical system. (a) M1; (2) M2; (c) L1 front; (d) L1 rear; (e) L2 front; (f) L2 rear
图 7 不同主、次镜间距变形系统示意图。（a）间距为80 mm；（b）间距为90 mm；（c）间距为100 mm
Figure 7. Schematic diagram of system with different spacings between the primary and secondary mirrors. Spacing is (a) 80 mm; (b) 90 mm; (c) 100 mm
图 8 不同主镜与次镜间距长度对应的（a）最大二向衰减及（b）最大相位延迟
Figure 8. (a) Maximum diattenuation and (b) maximum retardance corresponding to the spacing of the primary and secondary mirrors
图 9 出瞳面零视场的（a）二向衰减图及（b）相位延迟图（单位为度）
Figure 9. (a) Diattenuation map and (b) retardance at the exit pupil plane with zero field of view (the unit is degree)
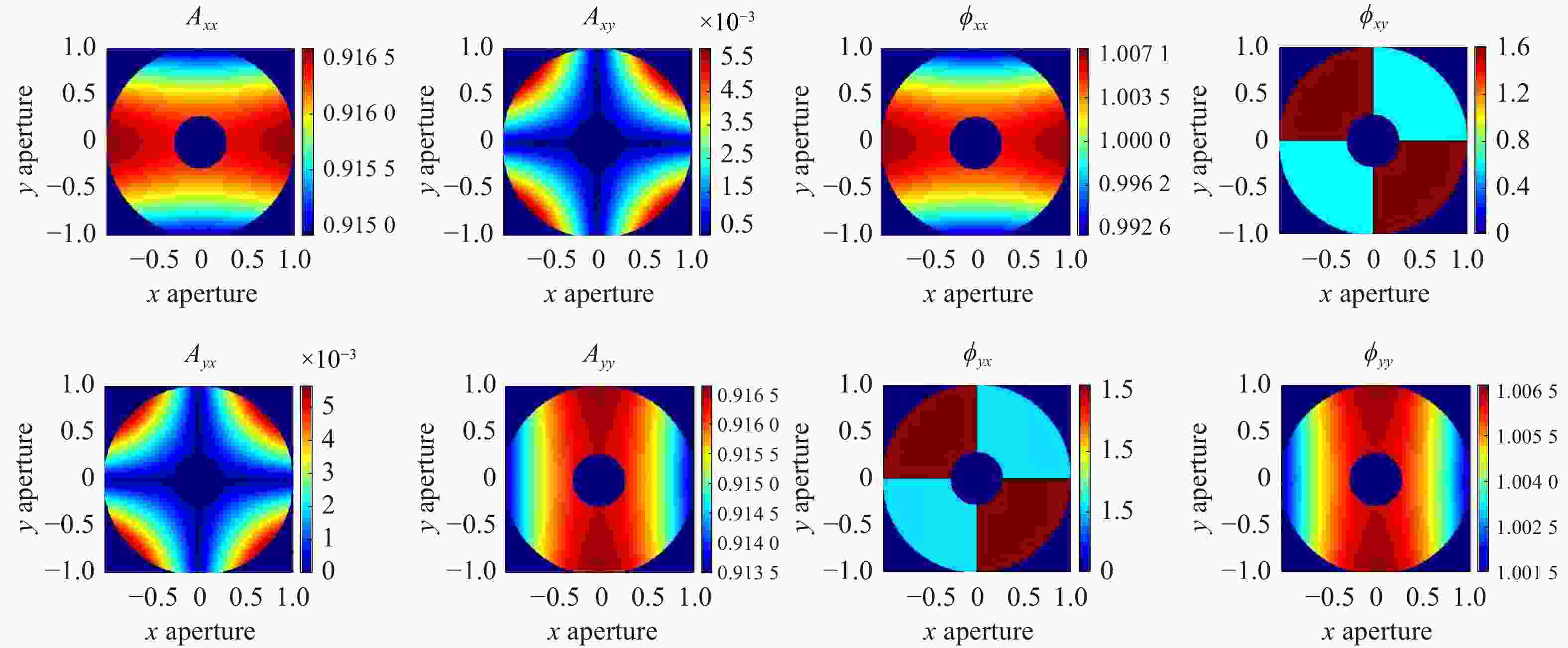
图 10 琼斯光瞳图。 Axx 、Axy、Ayx、Ayy伪色图的值表示透过率；
$\phi_{xx} $ 、$\phi_{xy} $ 、$\phi_{yx} $ 、$\phi_{yy} $ 伪色图的值表示相位变化量，单位为π radFigure 10. Jones pupil. The values of Axx, Axy, Ayx, Ayy denote the transmittance; the values of
$\phi_{xx} $ ,$\phi_{xy} $ ,$\phi_{yx} $ ,$\phi_{yy} $ denote the phase change in units of π rad
图 12 偏振像差影响下的变形光学系统点扩散函数。（a）Ixx点扩散函数；（b）Iyx点扩散函数；（c）Iyy点扩散函数；（d）Iyx点扩散函数
Figure 12. PSF of a anamorphic optical system under the influence of polarization. (a) Ixx PSF; (b) Iyx PSF; (c) Iyy PSF; (d) Iyx PSF
图 13 （a）沿着Ixx和Iyx的PSF图像对角线方向做截面上的归一化能量图；（b）沿着Iyy和Ixy的PSF图像对角线方向做截面上的归一化能量图
Figure 13. Normalized energy on the (a) cross-sections along the diagonal direction of the PSF images for Ixx and Iyx; (b) cross-sections along the diagonal direction of the PSF images for Iyy and Ixy
图 14 沿着Ixy和Iyx的PSF图像对角线方向做截面Ixy和Iyx归一化能量图
Figure 14. Normalized energy on the cross-sections along the diagonal direction of the PSF images for Ixy and Iyx
表 1 光学系统参数
Table 1. Parameters of optical system
参数 数值 波长/μm 0.48~0.65 F数 10 X方向视场角/(°) 1 Y方向视场角/(°) 0.5 X方向焦距/mm 1000 Y方向焦距/mm 500 X方向系统孔径/mm 50 Y方向系统孔径/mm 100 探测器阵列像素数 /pixel 2160 ×2160 探测器阵列尺寸/μm 6.61 
下载: 导出CSV
-
[1] CHIPMAN R, LAM W S T, YOUNG G. Polarized Light and Optical Systems[M]. Boca Raton: CRC Press, 2018. [2] CHIPMAN R A, LAM W S T, BRECKINRIDGE J. Polarization aberration in astronomical telescopes[J]. Proceedings of SPIE, 2015, 9613: 96130H. [3] BRECKINRIDGE J B, LAM W S T, CHIPMAN R A. Polarization aberrations in astronomical telescopes: the point spread function[J]. Publications of the Astronomical Society of the Pacific, 2015, 127(951): 445-468. doi: 10.1086/681280 [4] HE W J, FU Y G, LIU ZH Y, et al. Three-dimensional polarization aberration functions in optical system based on three-dimensional polarization ray-tracing calculus[J]. Optics Communications, 2017, 387: 128-134. doi: 10.1016/j.optcom.2016.11.046 [5] 罗敬, 何煦, 范阔, 等. 无遮拦离轴天文望远镜偏振像差分析及其对光学椭率的影响[J]. 光学学报,2020,40(8):0811001. doi: 10.3788/AOS202040.0811001LUO J, HE X, FAN K, et al. Polarization aberrations in an unobscured off-axis astronomical telescope and their effects on optics ellipticity[J]. Acta Optica Sinica, 2020, 40(8): 0811001. (in Chinese). doi: 10.3788/AOS202040.0811001 [6] 张艺蓝, 史浩东, 王超, 等. 离轴自由曲面光学系统偏振像差特性研究[J]. 光学学报,2021,41(18):1822002. doi: 10.3788/AOS202141.1822002ZHANG Y L, SHI H D, WANG CH, et al. Research on polarization aberration characteristics of off-axis freeform surface optical system[J]. Acta Optica Sinica, 2021, 41(18): 1822002. (in Chinese). doi: 10.3788/AOS202141.1822002 [7] LIU Y, LI Y Q, CAO ZH. Design of anamorphic magnification high-numerical aperture objective for extreme ultraviolet lithography by curvatures combination method[J]. Applied Optics, 2016, 55(18): 4917-4923. doi: 10.1364/AO.55.004917 [8] CHIPMAN R A. Polarization aberrations[D]. Tucson: The University of Arizona, 1987. [9] MCGUIRE J P, CHIPMAN R A. Polarization aberrations. Rotationally symmetric optical systems[J]. Applied Optics, 1994, 33(22): 5080-5100. doi: 10.1364/AO.33.005080 [10] SASIÁN J. Polarization fields and wavefronts of two sheets for understanding polarization aberrations in optical imaging systems[J]. Optical Engineering, 2014, 53(3): 035102. doi: 10.1117/1.OE.53.3.035102 [11] 杨宇飞, 颜昌翔, 胡春晖, 等. 相干激光通信光学系统偏振像差研究[J]. 光学学报,2016,36(11):1106003. doi: 10.3788/AOS201636.1106003YANG Y F, YAN CH X, HU CH H, et al. Polarization aberration analysis of coherent laser communication system[J]. Acta Optica Sinica, 2016, 36(11): 1106003. doi: 10.3788/AOS201636.1106003 [12] 王凯凯, 王超, 史浩东, 等. 含数字微镜器件的离轴光学系统偏振像差分析及补偿[J]. 光学学报,2022,42(16):1611001. doi: 10.3788/AOS202242.1611001WANG K K, WANG CH, SHI H D, et al. Polarization aberration analysis and compensation of off-axis optical system with digital micro-mirror device[J]. Acta Optica Sinica, 2022, 42(16): 1611001. doi: 10.3788/AOS202242.1611001 [13] 吴庆, 史广维, 张建萍, 等. 折反式变形光学系统设计[J]. 中国光学(中英文),2023,16(6):1376-1383. doi: 10.37188/CO.2023-0035WU Q, SHI G W, ZHANG J P, et al. Design of catadioptric anamorphic optical system[J]. Chinese Optics, 2023, 16(6): 1376-1383. (in Chinese). doi: 10.37188/CO.2023-0035 [14] 马迎军, 王晶, 洪永丰, 等. 道威棱镜的偏振特性及偏振补偿研究[J]. 中国光学,2016,9(1):137-143. doi: 10.3788/CO.20160901.0137MA Y J, WANG J, HONG Y F, et al. Polarization properties and polarization compensation of dove prism[J]. Chinese Optics, 2016, 9(1): 137-143. doi: 10.3788/CO.20160901.0137 [15] YUN G, CRABTREE K, CHIPMAN R A. Three-dimensional polarization ray-tracing calculus I: definition and diattenuation[J]. Applied Optics, 2011, 50(18): 2855-2865. doi: 10.1364/AO.50.002855 [16] BERNING P H. Theory and Calculation of Optical Thin Films[M]//HASS G. Physics of Thin Films. New York: Academic Press, 1963. [17] GEH B, RUOFF J, ZIMMERMANN J, et al. The impact of projection lens polarization properties on lithographic process at hyper-NA[J]. Proceedings of SPIE, 2007, 6520: 65200F. -
下载:
计量
- 文章访问数: 248
- HTML全文浏览量: 109
- PDF下载量: 50
- 被引次数: 0
