Orbital-angular-momentum spectra in coherent optical vortex beam arrays with hybrid states of polarization
doi: 10.37188/CO.EN-2023-0010
-
摘要:
轨道角动量(OAM)是高容量光通信和超分辨成像技术的重要参数。利用惠更斯-菲涅尔原理和相干合成理论,提出了杂化偏振涡旋合成光束阵列。详细研究了涡旋、偏振、附加拓扑电荷及子光束数对输入和输出平面光束的OAM谱的影响。结果表明:子光束的数量和杂化偏振共同影响了OAM模式的最大权重,子光束数量增加会显著提升OAM谱的最大权重,但杂化偏振却不能显著提升OAM谱的最大权重。OAM谱的最大模式位置总是等于光束中心光涡旋的总拓扑数,与子光束数无关。OAM谱所有非零权重模式的位置由涡旋、偏振、附加拓扑电荷和子光束数目共同决定。本文结果对光通信与偏振成像技术有着潜在的应用价值。
Abstract:Orbital-Angular-Momentum (OAM) is one of the most important parameters in high-capacity optical communication or super-resolution imaging. Based on the Huygens-Fresnel principle and the theory of coherent combination, we propose hybridly polarized vortex beam arrays in coherent combinations of radial off-axis Gaussian beamlets with vortex and polarization Topological Charges (TC). The effect of vortex, polarization and addition TC and the number of beamlets on OAM spectra of the proposed beam arrays at input and output plane are both stressed. The results show the number of beamlet and hybrid polarization present joint effect on maximal weight of OAM-modes. An increase of maximal weight value at OAM-mode is accompanied by the growing number of the beamlet, while the hybrid polarization can not significantly increase the maximum weight of OAM spectra. As the number of beamlets increases, hybrid polarization can't significantly improve the maximal weight value in OAM spectra. Furthermore, the maximal mode equals the total TC at central Optical Vortex (OV) and it is irrelevant to the number of beamlets. Whereas for other modes for non-zero weight, their locations are jointly determined by vortex, polarization and addition TCs and the number of beamlets. This work may provide potential applications in the OAM-based communication and polarization imaging technologies.
-
Key words:
- orbital angular momentum spectrum /
- polarization /
- vortex
-
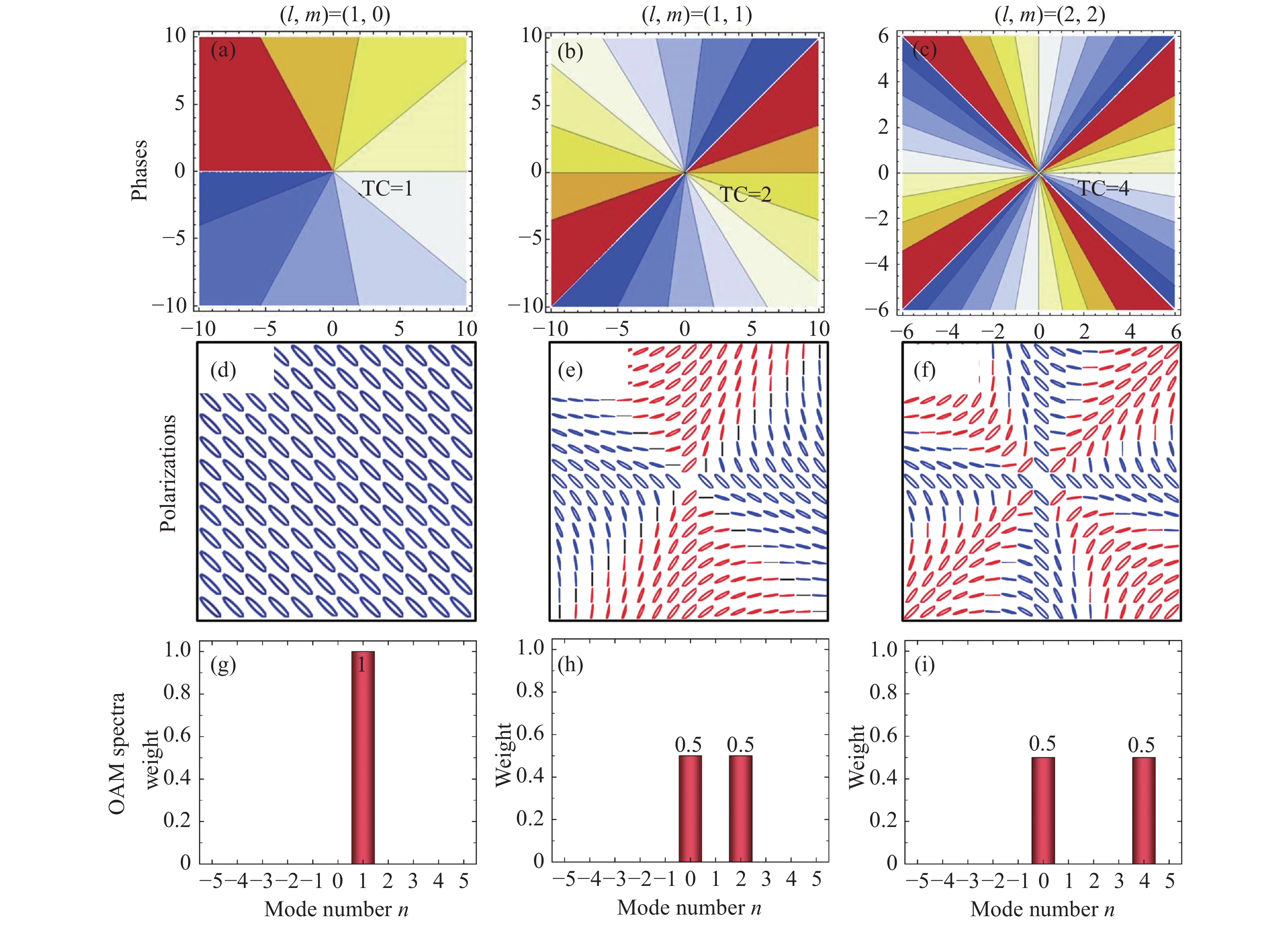
Figure 2. The OAM spectra (d)−(f) and OAM densities (g)−(i) of beam arrays in coherent combinations with radial, rectangular and linear symmetries at z=0. (a), (d), (g): radial symmetry; (b), (e), (h): rectangular symmetry; (c), (f), (i): linear symmetry. The parameters are (l, m)=(1, 1), η=0, N=6 and ρ=5w0
Table 1. The maximal weights of OAM spectra of the proposed beam arrays for different symmetry and beamlet numbers, the other parameters are the same as in Fig. 2
Symmetry N=4 N=6 N=8 Radial 0.221 0.333 0.432 Rectangular 0.198 0.201 0.174 Linear 0.119 0.106 0.065 -
[1] SHEN Y J, WANG X J, XIE ZH W, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities[J]. Light:Science & Applications, 2019, 8(1): 90. [2] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. doi: 10.1103/PhysRevA.45.8185 [3] BARREIRO J T, WEI T C, KWIAT P G. Beating the channel capacity limit for linear photonic superdense coding[J]. Nature Physics, 2008, 4(4): 282-286. doi: 10.1038/nphys919 [4] WILLNER A E, PANG K, SONG H, et al. Orbital angular momentum of light for communications[J]. Applied Physics Reviews, 2021, 8(4): 041312. doi: 10.1063/5.0054885 [5] EYYUBOĞLU H T. Mutual coherence function based topological charge detection in a Gaussian vortex beam optical communication system[J]. Physica Scripta, 2022, 97(9): 095507. doi: 10.1088/1402-4896/ac8956 [6] GRIER D G. A revolution in optical manipulation[J]. Nature, 2003, 424(6950): 810-816. doi: 10.1038/nature01935 [7] XIE G D, SONG H Q, ZHAO ZH, et al. Using a complex optical orbital-angular-momentum spectrum to measure object parameters[J]. Optics Letters, 2017, 42(21): 4482-4485. doi: 10.1364/OL.42.004482 [8] WANG Y L, WANG Y ZH, GUO ZH Y. OAM radar based fast super-resolution imaging[J]. Measurement, 2022, 189: 110600. doi: 10.1016/j.measurement.2021.110600 [9] MILIONE G, SZTUL H I, ALFANO R R. Propagation of a hybrid vector polarization beam in a uniaxial crystal[J]. Proceedings of SPIE, 2010, 7613: 76130I. doi: 10.1117/12.840769 [10] GU B, PAN Y, RUI G H, et al. Polarization evolution characteristics of focused hybridly polarized vector fields[J]. Applied Physics B, 2014, 117(3): 915-926. doi: 10.1007/s00340-014-5909-8 [11] LIAN M, GU B, ZHANG Y D, et al. Polarization rotation of hybridly polarized beams in a uniaxial crystal orthogonal to the optical axis: theory and experiment[J]. Journal of the Optical Society of America A, 2017, 34(1): 1-6. doi: 10.1364/JOSAA.34.000001 [12] CHEN R P, CHEW K H, DAI CH Q, et al. Optical spin-to-orbital angular momentum conversion in the near field of a highly nonparaxial optical field with hybrid states of polarization[J]. Physical Review A, 2017, 96(5): 053862. doi: 10.1103/PhysRevA.96.053862 [13] PENG Y M, XUE Y, XIAO G Z, et al. Spiral spectrum analysis and application of coherent synthetic vortex beams[J]. Acta Physica Sinica, 2019, 68(21): 214206. (in Chinese). doi: 10.7498/aps.68.20190880 [14] YANG Y J, ZHAO Q, LIU L L, et al. Manipulation of orbital-angular-momentum spectrum using pinhole plates[J]. Physical Review Applied, 2019, 12(6): 064007. doi: 10.1103/PhysRevApplied.12.064007 [15] ZHAO Q, DONG M, BAI Y H, et al. Measuring high orbital angular momentum of vortex beams with an improved multipoint interferometer[J]. Photonics Research, 2020, 8(5): 745-749. doi: 10.1364/PRJ.384925 [16] YANG L J, SUN SH, SHA W E I. Manipulation of orbital angular momentum spectrum using shape-tailored metasurface[J]. Advanced Optical Materials, 2021, 9(2): 2001711. doi: 10.1002/adom.202001711 [17] JIN ZH W, JANOSCHKA D, DENG J H, et al. Phyllotaxis-inspired nanosieves with multiplexed orbital angular momentum[J]. eLight, 2021, 1(1): 5. doi: 10.1186/s43593-021-00005-9 [18] BAI Y H, LV H R, FU X, et al. Vortex beam: generation and detection of orbital angular momentum [Invited][J]. Chinese Optics Letters, 2022, 20(1): 012601. doi: 10.3788/COL202220.012601 [19] SHU L Y, CHENG K, LIAO S, et al. Asymmetrical spiral spectra and orbital angular momentum density of non-uniformly polarized vortex beams in uniaxial crystals[J]. Chinese Physics B, 2023, 32(2): 024211. doi: 10.1088/1674-1056/ac7860 [20] WANG L G, WANG L Q, ZHU SH Y. Formation of optical vortices using coherent laser beam arrays[J]. Optics Communications, 2009, 282(6): 1088-1094. doi: 10.1016/j.optcom.2008.12.004 [21] KOTLYAR V V, KOVALEV A A. Optical vortex beams with a symmetric and almost symmetric OAM spectrum[J]. Journal of the Optical Society of America A, 2021, 38(9): 1276-1283. doi: 10.1364/JOSAA.432623 [22] TORNER L, TORRES J P, CARRASCO S. Digital spiral imaging[J]. Optics Express, 2005, 13(3): 873-881. doi: 10.1364/OPEX.13.000873 -






 下载:
下载: