基于纹理特征的图像复杂度研究

陈燕芹; 段锦; 祝勇; 钱小飞; 肖博

doi:10.3788/CO.20150803.0407

基于纹理特征的图像复杂度研究

doi: 10.3788/CO.20150803.0407

陈燕芹^{1, 3, ,},
段锦^{1, 3, ,},
祝勇^2, ,,
钱小飞^1, ,,
肖博^1, ,

1.
长春理工大学电子信息工程学院, 吉林长春 130022;
2.
长春理工大学计算机科学技术学院, 吉林长春 130022;
3.
长春理工大学空间光电技术研究所, 吉林长春 130022

基金项目: 国家高技术研究发展计划(863项目)资助项目(No.2013AA7XX10XX)

详细信息

通讯作者:
陈燕芹(1987-)，女，山东菏泽人，硕士研究生，2012年于滨州学院获得学士学位，主要从事模式识别和图像复杂度方面的研究。E-mail:chenyanqin101329@sina.com

段锦(1971-)，男，吉林长春人，教授，博士生导师，1993年于北京理工大学获得学士学位,1998年于沈阳工业学院获得硕士学位，2004年于吉林大学获得博士学位，主要从事图像处理、模式识别、光电检测等方面的研究。E-mail:duanjin@vip.sina.com

祝勇(1980-)，男，四川眉山人，讲师，主要从事计算机仿真、图像处理、模式识别方面的研究。E-mail:zhy991112@sina.com

钱小飞(1987-)，男，内蒙古人，硕士研究生，主要从事图像目标检测与识别方面的研究。E-mail:qjf0805@163.com

肖博(1987-)，男，新疆乌鲁木齐人，博士研究生，2009年于吉林大学获得学士学位，2013年于长春理工大学获得硕士学位，主要从事图像目标识别和图像复杂度方面的研究。E-mail:706992535@qq.com

中图分类号: TP391.4
计量
- 文章访问数: 2295
- HTML全文浏览量: 407
- PDF下载量: 1144
- 被引次数: 0
出版历程
- 收稿日期: 2014-11-15
- 录用日期: 2015-01-17
- 刊出日期: 2015-01-25

Research on the image complexity based on texture features

CHEN Yan-qin^{1, 3
, ,},
DUAN Jin^{1, 3
, ,},
ZHU Yong^{2
, ,},
QIAN Xiao-fei^{1
, ,},
XIAO Bo^{1
, ,}

1.
School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China;
2.
School of Computer Science and Technology, Changchun University of Science and Technology, Changchun 130022, China;
3.
Institute of Space Optoelectronics Technology, Changchun University of Science and Technology, Changchun 130022, China

摘要

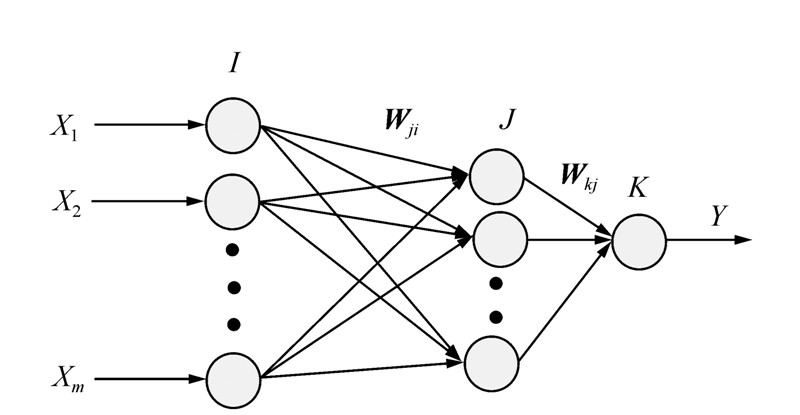
摘要: 为了更好地描述图像内部的复杂程度,建立图像复杂度与各指标之间的数学模型是研究图像复杂度最关键的一步。首先从图像纹理出发,试图建立图像复杂度与各指标之间定量、精确的数学关系描述。针对目前图像复杂度与各衡量指标之间没有明确的数学关系的特点,文中采用灰度共生矩阵对纹理的主要特征参数进行分析,提出了基于BP神经网络的图像复杂度评价方法,建立了图像复杂度与各个指标之间非线性的数学评价模型。通过大量的图片对神经网络进行训练学习,得到各指标的权重值。验证结果表明,所建评价模型能够真实地反映图像内部的复杂程度,获得的实验结果与人类视觉感知的结果基本一致。对于将BP神经网络应用于图像复杂度的研究具有一定的参考价值。
- 图像复杂度 /
- 纹理特征 /
- 灰度共生矩阵 /
- BP神经网络 /
- 权重系数
Abstract: In order to better describe the internal complexity of image, the establishment of the mathematic model between the image complexity and each index is the key step to study the complexity of image. Firstly, starting from the image texture, we try to establish a quantitative and precise mathematical description of the relationship between the image and the complexity of various indicators. There is no clear mathematical relationship between the image complexity and the measurable indicators, so gray level co-occurrence matrix(GLCM) is used to analyze the main characteristic parameters of the texture. The image complexity evaluation method is proposed based on BP neural network. Then a nonlinear mathematical evaluation model between image complexity and each index is established. And the weight values and index are obtained by the training for the neural network and learning through numbers of pictures. The verification results show that the evaluation model is able to reflect the internal complexity of the image truly, and the experimental results obtained are consistent with human visual perception. It is of a certain reference value for the application of BP neural network to study the image complexity.
- image complexity /
- texture feature /
- Gray Level Co-occurrence Matrix /
- BP neural network /
- weight value

HTML全文

图 1 BP网络模型

Figure 1. BP network model

下载: 全尺寸图片幻灯片

图 2 不同等级复杂度的测试图片

Figure 2. Test images of different levels of complexity

下载: 全尺寸图片幻灯片

图 3 图像复杂度3种结果比较

Figure 3. Comparison of three image complexity results

下载: 全尺寸图片幻灯片

表 1 图像复杂度等级划分

Table 1. Image complexity classification

下载: 导出CSV

表 2 图像纹理评价各神经网络参数表

Table 2. Image texture evaluation of the neural network parameter table

下载: 导出CSV

表 3 图像纹理BP神经网络训练的样本数据

Table 3. Sample data of image texture and the training of BP neural network

下载: 导出CSV

表 4 图像复杂度评价指标权重

Table 4. Weights of image complexity evaluation index

下载: 导出CSV

表 5 本文方法与文献^[4]方法对比表

Table 5. Comparison of the method proposed in this paper with the method in literature^[4] proposed in this paper

下载: 导出CSV