Femtosecond pulse compression using negative-curvature hollow-core fibers
doi: 10.3788/CO.20191201.0075
-
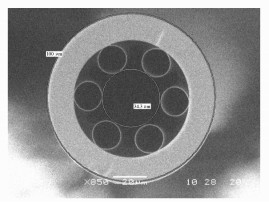
摘要: 为了实现对飞秒激光器产生的超短脉冲的进一步压缩,对近年来出现的一种新型负曲率空芯光纤展开了研究,并基于该光纤对800 nm飞秒激光进行了压缩实验。首先介绍了一种圆形玻璃管包层结构的负曲率空芯光纤,通过有限元方法对光纤的损耗特性进行计算,并与实验测试结果进行对比。然后利用广义非线性薛定谔方程对脉冲在光纤中的传输进行了模拟仿真。最后利用该光纤进行了超短脉冲压缩实验,将脉冲宽度为160 fs的钛宝石飞秒激光耦合进一段充高压氩气的圆形玻璃管包层结构的负曲率空芯光纤,通过光纤内反常色散和自相位调制的共同作用,得到84 fs的输出,实现脉冲的压缩,实验结果与仿真计算一致。这种新型的负曲率空芯光纤损伤阈值高、色散、非线性系数小且灵活可调,非常适用于超快领域研究。Abstract: In order to compress femtosecond ultrashort pulses, a novel fiber called negative-curvature hollow-core fiber, is investigated and is used to compress the output of a Ti:Sapphire laser. Firstly, a hollow-core fiber with circular tubes cladding is introduced, and the loss parameter is calculated with the Finite Element Method and the calculated results are compared with the experimental results. Following this, the evolution of an ultrashort pulse along the fiber is simulated in the General Nonlinear Schrodinger Equation. At last the compression experiment using NC-HCF is conducted. The 160 fs output of a Ti:Sapphire laser is coupled into the fiber with high-pressure Argon. An output of 84 fs is achieved, which is the result of the balance between anomalous dispersion and self-phase modulation in the fiber. The experimental results matched the simulations. This novel fiber, which has the advantages of a high damage threshold, low and adjustable dispersion and nonlinear coefficients, is a promising material in the field of ultrafast optics.
-
Key words:
- negative-curvature /
- hollow-core fiber /
- pulse compression
-
图 5 广义非线性薛定谔方程对脉冲在光纤中演变的计算结果. (a)为z=0.5 m时脉冲的频谱分布; (b)为z=0.5 m时脉冲的时域分布; (c)为脉冲在0.5 m长的负曲率空芯光纤中传输时的频域分布; (d)为脉冲在0.5 m长的负曲率空芯光纤中传输时的时域分布
Figure 5. The calculated evolution of the ultrafast pulse in the NC-HCF with GNLSE. (a)The spectrum output of 0.5 m NC-HCF; (b)The temporary output of the 0.5 m NC-HCF; (c)The spectrum evolution of the 160 fs pulse propagating along the 0.5 m NC-HCF; (d)The temporary evolution of the 160 fs pulse propagating along the 0.5 m NC-HCF
-
[1] PRYAMIKOV A D, BIRIUKOV A S, KOSOLAPOY A F, et al..Demonstration of a waveguide regime for a silica hollow-core microstructured optical fiber with a negative curvature of the core boundary in the spectral region >3.5μm[J].Opt.Express, 2011, 19(2):1441-1448. doi: 10.1364/OE.19.001441 [2] WANG Y Y, COUNY F, ROBOERS P J, et al..Low loss broadband transmission in optimized core-shape Kagome hollow-core PCF[C].2010 Laser Science to Photonic Applications, San Jose, USA: CLEO, 2010: 1-2. [3] JAWORSKI P, YU F, MAIER R R J, et al..Picosecond and nanosecond pulse delivery through a hollow-core negative curvature fiber for micro-machining applications[J].Opt.Express, 2013, 21(19):22742-22753. doi: 10.1364/OE.21.022742 [4] KOLYADIN A.N, ALAGASHEV G K, PRYAMIKOV A D, et al..Negative curvature hollow-core fibers:dispersion properties and femtosecond pulse delivery[J].Physics Procedia, 2015, 73:59-66. doi: 10.1016/j.phpro.2015.09.122 [5] MICHIELETTO M, LYNGSE J K, JAKOBSEN C, et al..Hollow-core fibers for high power pulse delivery[J].Opt.Express, 2016, 24(7):7103-7119. doi: 10.1364/OE.24.007103 [6] POLETTI F.Nested antiresonant nodeless hollow core fiber[J].Opt.Express, 2014, 22(20):23807-23828. doi: 10.1364/OE.22.023807 [7] HABIB M S, BANG O, BACHE M.Low-loss single-mode hollow-core fiber with anisotropic anti-resonant elements[J].Opt.Express, 2016, 24(8):8429-8436. doi: 10.1364/OE.24.008429 [8] MENG F C, LIU B W, LI Y F, et al..Low loss hollow-core antiresonant fiber with nested elliptical cladding elements[J].IEEE Photonics Journal, 2017, 9(1):1-11. [9] 高寿飞, 汪莹莹, 刘小璐, 等.空芯反谐振光纤及其高功率超短脉冲传输[J].中国激光, 2017, 44(2):0201012.GAO SH F, WANG Y Y, LIU X L, et al..Hollow-core anti-resonant fiber and its use for propagation of high power ultrafast pulse[J].Chinese Journal of Lasers, 2017, 44(2):0201012.(in Chinese) [10] GEHBARDT M, GAIDA C, HEUERMANN T, et al..Nonlinear pulse compression to 43 W GW-class few-cycle pulses at 2μm wavelength[J].Optics Lett., 2017, 42(20):4179-4182. doi: 10.1364/OL.42.004179 [11] AZHAR M, WONG G K L, CHANG W, et al..Raman-free nonlinear optical effects in high pressure gas-filled hollow core PCF[J].Opt.Express, 2013, 21(4):4405-4410. doi: 10.1364/OE.21.004405 [12] GEROME F, DUPRIEZ P, CLOWES J, et al..High power tunable femtosecond soliton source using hollow-core photonic bandgap fiber, and its use for frequency doubling[J].Opt.Express, 2008, 16(4):2381-2386. doi: 10.1364/OE.16.002381 [13] LU J, HUANG ZH Y, WANG D, et al..Nonlinear compression of picosecond chirped pulse from thin-disk amplifier system through a gas-filled hollow-core fiber[J].Chinese Physics B, 2016, 25(12):124207. doi: 10.1088/1674-1056/25/12/124207 [14] GEBHARDT M, GAIDA C, STUTZKI F, et al..High average power nonlinear self-compression to few-cycle pulses at 2μm wavelength in antiresonant hollow-core fiber[C].Advanced Solid State Lasers Congress, Nagoya, Japan: ASSL, 2017: ATh3A.6. [15] ZURCH M, SOLLAPUR R, KARTASHOV D, et al..Multi-octave supercontinuum driven by soliton explosion in dispersion-designed antiresonant hollow-core fibers[C].Lasers and Electro-Optics, San Jose, USA: CLEO, 2017: 1-2. [16] GONZALEZ B N, TORRES G I, ARZATE N, et al..Pulse quality analysis on soliton pulse compression and soliton self-frequency shift in a hollow-core photonic bandgap fiber[J].Opt.Express, 2013, 21(7):9132-9143. doi: 10.1364/OE.21.009132 [17] LEGSGAARD J, ROBERTS P J.Dispersive pulse compression in hollow-core photonic bandgap fibers[J].Opt.Express, 2008, 16(13):9628-9644. doi: 10.1364/OE.16.009628 [18] 乔自文, 高炳荣, 陈岐岱, 等.飞秒超快光谱技术及其互补使用[J].中国光学, 2014, 7(4):588-599. http://www.chineseoptics.net.cn/CN/abstract/abstract9168.shtmlQIAO Z W, GAO B R, CHEN Q D, et al..Ultrafast spectroscopy techniques and their complementary usages[J].Chinese Optics, 2014, 7(4):588-599.(in Chinese) http://www.chineseoptics.net.cn/CN/abstract/abstract9168.shtml [19] EMAURY F, DUTIN C F, SARACENO C J, et al..Beam delivery and pulse compression to sub-50 fs of a mode locked thin-disk laser in a gas-filled Kagome-type HC-PCF fiber[J].Opt.Express, 2013, 21(4):4986-4994. doi: 10.1364/OE.21.004986 [20] MAK K F, SEIDEL M, PRONIN O, et al..Compressing μJ-level pulses from 250 fs to sub-10 fs at 38-MHz repetition rate using two gas-filled hollow-core photonic crystal fiber stages[J].Opt.Lett., 2015, 40(7):1238-1241. doi: 10.1364/OL.40.001238 [21] AGRAWAL G P.Nonlinear Fiber Optics[M].Heidelberg:Springer Berlin Heidelberg, 2000. [22] DUGUAY M A, KOKUBUN Y, KOCH T L, et al..Antiresonant reflecting optical waveguides in SiO2-Si multilayer structures[J].Appl.Phys.Lett., 2002, 49(18):1592-1594. [23] JOHN L.光导在折射率引导光纤、多孔光纤、光子带隙光纤和纳米线中的简要定性解释[J].中国光学, 2014, 7(3):499-508.(in English) http://www.chineseoptics.net.cn/CN/abstract/abstract9155.shtmlJOHN L.Simple qualitative explanations for light guidance in index-guiding fibres, holey fibres, photonic band-gap fibres and nanowires[J].Chinese Optics, 2014, 7(3):499-508. http://www.chineseoptics.net.cn/CN/abstract/abstract9155.shtml [24] POLYANSKIY M N.Refractive index database.https://refractiveindex.info[OL]. [25] SMITH A V, DO B T.Bulk and surface laser damage of silica by picosecond and nanosecond pulses at 1064 nm[J].Appl.Opt., 2008, 47(26):4812-4832. doi: 10.1364/AO.47.004812 [26] 王竞, 李健中, 温伟峰, 等.利用自相关方法实现光脉冲时间延迟精确测量[J].中国光学, 2015, 8(2):270-276. http://html.rhhz.net/ZGGX/html/gx20150214.htmWANG J, LI J ZH, WEN W F, et al..Precisely measuring for optical pulse time delay using autocorrelation[J].Chinese Optics, 2015, 8(2):270-276.(in Chinese) http://html.rhhz.net/ZGGX/html/gx20150214.htm [27] 陈雪坤, 张璐, 吴志勇.空间激光与单模光纤和光子晶体光纤的耦合效率[J].中国光学, 2013, 6(2):208-215. http://www.chineseoptics.net.cn/CN/abstract/abstract8891.shtmlCHEN X K, ZHANG L, WU ZH Y.Coupling efficiency of free-space laser coupling into single mode fiber and photonic crystal fiber[J].Chinese Optics, 2013, 6(2):208-215.(in Chinese) http://www.chineseoptics.net.cn/CN/abstract/abstract8891.shtml -






 下载:
下载: