Quantum key distribution based on heterogeneous air-water channels with foam-covered irregular sea surfaces
-
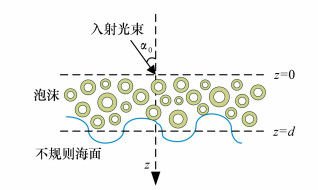
摘要: 针对空-水量子密钥分发（Quantum Key Distribution，QKD），综合考虑海风影响、泡沫覆盖的不规则海面、空-水信道复杂多变性和量子偏振态多重散射过程，建立了非均匀空-水信道复合模型。据此完善了空-水QKD系统量子误码率理论模型，并采用偏振矢量蒙特卡罗算法模拟，详细分析了不同海洋环境下非均匀空-水信道光量子传输性能，及空-水QKD整体传输性能。结果表明：清澈海水条件下的非均匀空-水信道可实现水下百米量级的密钥分发，但风速和传输距离的增大都会导致光子退偏比增大，保真度减小，偏振误码率增加；同时风速和泡沫层厚度的增大也会造成空-水QKD系统量子误码率上升，密钥生成率和传输距离下降，且随信号波长的增加这两者也会增加，在波长为532 nm，信道由最佳（无风无泡沫）变至最差（暴风且泡沫层为6 cm）时，水下传输距离由120.8 m缩减至85 m，基本能保障水下航行器百米级的安全潜深，而采用拖拽浮标等措施又可进一步增加空-水QKD的安全距离。由此验证了泡沫覆盖不规则海面下非均匀空-水信道诱骗态QKD的可行性，对未来空-水一体量子通信链路的实现具有参考价值。Abstract: For air-water Quantum Key Distribution(QKD), considering the effects of sea breeze, irregular sea surfaces with foam, the complicacy and variety of air-water channels and multiple scattering processes of the polarized quantum state, a heterogeneous air-water channel composite model is established. Based on this, the theoretical model of the error rate of air-water QKD systems is improved. Then, through a polarization vector Monte Carlo simulation, the transmission characteristics of photons in heterogeneous air-water channels and the overall transmission performance of air-water QKDs under different marine environments are analyzed in detail. The results show that heterogeneous air-water channels under clear seawater conditions can achieve a key distribution of 100 meters underwater, but the increase of wind speed and transmission distance will lead to an increase in the photon depolarization ratio and a decrease in fidelity, thereby increasing the polarization error rate. Meanwhile, the rise of wind speed and foam layer thickness adds the quantum error rate of air-water QKD systems and decreases the key generation rate and transmission distance. Both of these factors increase with an increase in signal wavelength. When the wavelength is 532 nm and the channel changes from best(no wind and foam) to worst(storm and foam layer thickness of 6 cm) conditions, the underwater transmission distance is shortened from 120.8 m to 85 m. It can guarantee a 100 m safety depth in underwater vehicles and alternate contingencies such as dragging the buoy can further increase the safety distance of air-water QKD. Therefore, this paper verifies the feasibility of a decoy QKD in a heterogeneous air-water channel with a foam-irregular sea surface and acts as a significant reference for future technologies in air-water integrated quantum communication links.
-
图 4 多层大气/海水信道模型的光传输图示
Figure 4. Schematic diagram of beam propagation in the multilayer atmospheric/seawater channel model
图 6 不同海水中，光衰减随传输距离的变化
Figure 6. Light attenuation varies with transmission distance in different sea waters
图 7 不同风速下的光子退偏比和保真度
Figure 7. Depolarization ratio and fidelity of the photon at different wind speeds
图 10 不同泡沫层厚度下，密钥生成率随传输距离的变化情况
Figure 10. Key generation rate varies with transmission distance at different foam thicknesses
图 11 不同波长下，密钥生成率随传输距离的变化
Figure 11. Key generation rate varies with transmission distance at different wavelengths
表 1 主要仿真参数设置
Table 1. The main simulation parameters
参数 取值 参数 取值 Idc 60 Hz FOV 174 mrad λ 532 nm Δλ 0.12×10-9 nm Δt 35 ns Δt′ 200 ps A 20 cm2 ηB 0.3 
下载: 导出CSV
-
[1] 张冬辰, 周吉.军事通信[M]. 2版.北京:国防工业出版社, 2008.ZHANG D CH, ZHOU J. Military Communications[M]. 2nd ed. Beijing:National Defense Industry Press, 2008.(in Chinese) [2] LANZAGORTA M. Underwater Communications[M]. California:Morgan & Claypool, 2012. [3] BENNETT C H, BRASSARD G. Quantum cryptography: public key distribution and coin tossing[C]. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, IEEE, 1984: 175-179. [4] LO H K, CURTY M, QI B. Measurement-device-independent quantum key distribution[J]. Physical Review Letters, 2012, 108(13):130503. doi: 10.1103/PhysRevLett.108.130503 [5] KORZH B, LIM C C W, HOULKANN R, et al.. Provably secure and practical quantum key distribution over 307 km of optical fibre[J]. Nature Photonics, 2015, 9(3):163-168. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=233b7b241043c7e2d29bac9051c3d62e [6] YIN H L, CHEN T Y, YU Z W, et al.. Measurement-device-independent quantum key distribution over a 404 km optical fiber[J]. Physical Review Letters, 2016, 117(19):190501. doi: 10.1103/PhysRevLett.117.190501 [7] LIU L, GUO F ZH, WEN Q Y. Practical passive decoy state measurement-device-independent quantum key distribution with unstable sources[J]. Scientific Reports, 2017, 7(1):11370. doi: 10.1038/s41598-017-09367-y [8] 彭承志, 潘建伟.量子科学实验卫星—"墨子号"[J].中国科学院院刊, 2016, 31(9):1096-1104. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgkxyyk201609015PENG CH ZH, PAN J W. Quantum science experimental satellite "Micius"[J]. Bulletin of the Chinese Academy of Sciences, 2016, 31(9):1096-1104.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgkxyyk201609015 [9] YIN J, CAO Y, LI Y H, et al.. Satellite-to-ground entanglement-based quantum key distribution[J]. Physical Review Letters, 2017, 119(20):200501. doi: 10.1103/PhysRevLett.119.200501 [10] LIAO SH K, YONG H L, LIU CH, et al.. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication[J]. Nature Photonics, 2017, 11(8):509-513. doi: 10.1038/nphoton.2017.116 [11] LIAO SH K, CAI W Q, LIU W Y, et al.. Satellite-to-ground quantum key distribution[J]. Nature, 2017, 549(7670):43-47. doi: 10.1038/nature23655 [12] ZHAI P W, KATTAWAR G W, YANG P. Impulse response solution to the three-dimensional vector radiative transfer equation in atmosphere-ocean systems.Ⅱ.the hybrid matrix operator-Monte Carlo method[J]. Applied Optics, 2008, 47(8):1063-1071. doi: 10.1364/AO.47.001063 [13] 魏安海.光脉冲在大气-海水混合信道中传输特性研究[D].西安: 中国科学院研究生院(西安光学精密机械研究所), 2014.WEI A H. Simulative study of optical pulse propagation properties in atmosphere-seawater hybrid channel[D]. Xi'an: Xi'an Institute of Optics and Precision Mechanics Chinese Academy of Science, 2014.(in Chinese) [14] 李祥震, 苗希彩, 亓晓, 等.复杂海况下激光气-海信道传输特性[J].光学学报, 2018, 38(3):0301002. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201803023LI X ZH, MIAO X C, QI X, et al.. Laser atmosphere-seawater channel transmission characteristics under complicated sea conditions[J]. Acta Optica Sinica, 2018, 38(3):0301002.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201803023 [15] 周飞, 雍海林, 李东东, 等.基于不同介质间量子密钥分发的研究[J].物理学报, 2014, 63(14):140303. doi: 10.7498/aps.63.140303ZHOU F, YONG H L, LI D D, et al.. Study on quantum key distribution betweem different media[J]. Acta Physica Sinica, 2014, 63(14):140303.(in Chinese) doi: 10.7498/aps.63.140303 [16] UHLMANN J, LANZAGORTA M, VENEGAS-ANDRACA S E. Quantum communications in the maritime environment[C]. OCEANS 2015-MTS/IEEE Washington, IEEE, 2015. [17] SHI P, ZHAO SH CH, LI W D, et al.. Feasibility of underwater free space quantum key distribution[J]. arXiv preprint arXiv: arXiv: 1402.4666, 2014. [18] SHI P, ZHAO SH CH, GU Y J, et al.. Channel analysis for single photon underwater free space quantum key distribution[J]. Journal of the Optical Society of America A, 2015, 32(3):349-356. doi: 10.1364/JOSAA.32.000349 [19] JI L, GAO J, YANG A L, et al.. Towards quantum communications in free-space seawater[J]. Optics Express, 2017, 25(17):19795-19806. doi: 10.1364/OE.25.019795 [20] 王潋, 周媛媛, 周学军, 等.泡沫覆盖不规则海面的空-水量子密钥分发[J].光学学报, 2018, 38(10):1027002. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201810045WANG L, ZHOU Y Y, ZHOU X J, et al.. Air-water quantum key distribution on irregular sea surface covered with foams[J]. Acta Optica Sinica, 2018, 38(10):1027002.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201810045 [21] GJERSTAD K I, STAMNES J J, HAMRE B, et al.. Monte Carlo and discrete-ordinate simulations of irradiances in the coupled atmosphere-ocean system[J]. Applied Optics, 2003, 42(15):2609-2622. doi: 10.1364/AO.42.002609 [22] WU J. Bubble flux and marine aerosol spectra under various wind velocities[J]. Journal of Geophysical Research:Oceans, 1992, 97(C2):2327-2333. doi: 10.1029/91JC02568 [23] 亓晓.泡沫覆盖气-海界面的激光传输特性[D].西安: 西安电子科技大学, 2015: 46-48.QI X. Propagation characteristics of laser beam traversing the air-sea interface with foams[D]. Xi'an: Xidian University, 2015: 46-48.(in Chinese) [24] 黄文超.蓝绿激光通过粗糙海面的传输特性研究[D]: 西安: 西安电子科技大学, 2012;HUANG W CH. Study of the character of blue-green laser transmission through sea surface[D]. Xi'an: Xidian University, 2012.(in Chinese) [25] GOOCH J W. Snell's Law[M]. New York:Springer, 2011:673-675. [26] 李景镇.光学手册[M].西安:陕西科学技术出版社, 2010.LI J ZH. Handbook of Optics[M]. Xi'an:Shanxi Science and Technology Press, 2010.(in Chinese) [27] ZENG ZH Q, FU SH, ZHANG H H, et al., A survey of underwater optical wireless communications[J]. IEEE Communications Surveys & Tutorials, 2017, 19(1):204-238. [28] GAWDI Y J. Underwater free space optics[D]. Raleigh: North Carolina State University, 2006. [29] JOHNSON L J, GREEN R J, LEESON M S. Underwater optical wireless communications:depth dependent variations in attenuation[J]. Applied Optics, 2013, 52(33):7867-7873. doi: 10.1364/AO.52.007867 [30] ZHAI P W, HU Y S, CHOWDHARY J, et al.. A vector radiative transfer model for coupled atmosphere and ocean systems with a rough interface[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2010, 111(7-8):1025-1040. doi: 10.1016/j.jqsrt.2009.12.005 [31] WU Z S, WANG Y P. Electromagnetic scattering for multilayered sphere: recursive algorithms[J]. Radio Science, 1991, 26(6):1393-1401. doi: 10.1029/91RS01192 [32] TSANG L, DING K H, ZHANG G F, et al.. Backscattering enhancement and clustering effects of randomly distributed dielectric cylinders overlying a dielectric half space based on Monte-Carlo simulations[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(5):488-499. doi: 10.1109/8.384193 [33] KALOS M H, JACQUES S L. Monte Carlo Methods[M]. New Jersey:John Wiley & Sons, 2008. [34] ZHOU Y H, YU Z W, WANG X B. Tightened estimation can improve the key rate of measurement-device-independent quantum key distribution by more than 100%[J]. Physical Review A, 2014, 89(5):052325. doi: 10.1103/PhysRevA.89.052325 -
下载:
图(11) / 表(1)
计量
- 文章访问数: 1563
- HTML全文浏览量: 565
- PDF下载量: 37
- 被引次数: 0
